The PHREG Procedure
- Overview
-
Getting Started

-
Syntax
 PROC PHREG StatementASSESS StatementBASELINE StatementBAYES StatementBY StatementCLASS StatementCONTRAST StatementEFFECT StatementESTIMATE StatementFREQ StatementHAZARDRATIO StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementProgramming StatementsRANDOM StatementSTRATA StatementSLICE StatementSTORE StatementTEST StatementWEIGHT Statement
PROC PHREG StatementASSESS StatementBASELINE StatementBAYES StatementBY StatementCLASS StatementCONTRAST StatementEFFECT StatementESTIMATE StatementFREQ StatementHAZARDRATIO StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementProgramming StatementsRANDOM StatementSTRATA StatementSLICE StatementSTORE StatementTEST StatementWEIGHT Statement -
Details
 Failure Time DistributionTime and CLASS Variables UsagePartial Likelihood Function for the Cox ModelCounting Process Style of InputLeft-Truncation of Failure TimesThe Multiplicative Hazards ModelProportional Rates/Means Models for Recurrent EventsThe Frailty ModelProportional Subdistribution Hazards Model for Competing-Risks DataHazard RatiosNewton-Raphson MethodFirth’s Modification for Maximum Likelihood EstimationRobust Sandwich Variance EstimateTesting the Global Null HypothesisType 3 Tests and Joint TestsConfidence Limits for a Hazard RatioUsing the TEST Statement to Test Linear HypothesesAnalysis of Multivariate Failure Time DataModel Fit StatisticsSchemper-Henderson Predictive MeasureResidualsDiagnostics Based on Weighted ResidualsInfluence of Observations on Overall Fit of the ModelSurvivor Function EstimatorsCaution about Using Survival Data with Left TruncationEffect Selection MethodsAssessment of the Proportional Hazards ModelThe Penalized Partial Likelihood Approach for Fitting Frailty ModelsSpecifics for Bayesian AnalysisComputational ResourcesInput and Output Data SetsDisplayed OutputODS Table NamesODS Graphics
Failure Time DistributionTime and CLASS Variables UsagePartial Likelihood Function for the Cox ModelCounting Process Style of InputLeft-Truncation of Failure TimesThe Multiplicative Hazards ModelProportional Rates/Means Models for Recurrent EventsThe Frailty ModelProportional Subdistribution Hazards Model for Competing-Risks DataHazard RatiosNewton-Raphson MethodFirth’s Modification for Maximum Likelihood EstimationRobust Sandwich Variance EstimateTesting the Global Null HypothesisType 3 Tests and Joint TestsConfidence Limits for a Hazard RatioUsing the TEST Statement to Test Linear HypothesesAnalysis of Multivariate Failure Time DataModel Fit StatisticsSchemper-Henderson Predictive MeasureResidualsDiagnostics Based on Weighted ResidualsInfluence of Observations on Overall Fit of the ModelSurvivor Function EstimatorsCaution about Using Survival Data with Left TruncationEffect Selection MethodsAssessment of the Proportional Hazards ModelThe Penalized Partial Likelihood Approach for Fitting Frailty ModelsSpecifics for Bayesian AnalysisComputational ResourcesInput and Output Data SetsDisplayed OutputODS Table NamesODS Graphics -
Examples
 Stepwise RegressionBest Subset SelectionModeling with Categorical PredictorsFirth’s Correction for Monotone LikelihoodConditional Logistic Regression for m:n MatchingModel Using Time-Dependent Explanatory VariablesTime-Dependent Repeated Measurements of a CovariateSurvival CurvesAnalysis of ResidualsAnalysis of Recurrent Events DataAnalysis of Clustered DataModel Assessment Using Cumulative Sums of Martingale ResidualsBayesian Analysis of the Cox ModelBayesian Analysis of Piecewise Exponential ModelAnalysis of Competing-Risks Data
Stepwise RegressionBest Subset SelectionModeling with Categorical PredictorsFirth’s Correction for Monotone LikelihoodConditional Logistic Regression for m:n MatchingModel Using Time-Dependent Explanatory VariablesTime-Dependent Repeated Measurements of a CovariateSurvival CurvesAnalysis of ResidualsAnalysis of Recurrent Events DataAnalysis of Clustered DataModel Assessment Using Cumulative Sums of Martingale ResidualsBayesian Analysis of the Cox ModelBayesian Analysis of Piecewise Exponential ModelAnalysis of Competing-Risks Data - References
Specifics for Bayesian Analysis
To request a Bayesian analysis, you specify the new BAYES statement in addition to the PROC PHREG statement and the MODEL statement. You include a CLASS statement if you have effects that involve categorical variables. The FREQ or WEIGHT statement can be included if you have a frequency or weight variable, respectively, in the input data. The STRATA statement can be used to carry out a stratified analysis for the Cox model, but it is not allowed in the piecewise constant baseline hazard model. Programming statements can be used to create time-dependent covariates for the Cox model, but they are not allowed in the piecewise constant baseline hazard model. However, you can use the counting process style of input to accommodate time-dependent covariates that are not continuously changing with time for the piecewise constant baseline hazard model and the Cox model as well. The HAZARDRATIO statement enables you to request a hazard ratio analysis based on the posterior samples. The ASSESS, CONTRAST, ID, OUTPUT, and TEST statements, if specified, are ignored. Also ignored are the COVM and COVS options in the PROC PHREG statement and the following options in the MODEL statement: BEST=, CORRB, COVB, DETAILS, HIERARCHY=, INCLUDE=, MAXSTEP=, NOFIT, PLCONV=, SELECTION=, SEQUENTIAL, SLENTRY=, and SLSTAY=.
Piecewise Constant Baseline Hazard Model
Single Failure Time Variable
Let 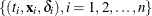 be the observed data. Let
be the observed data. Let 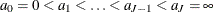 be a partition of the time axis.
be a partition of the time axis.
Hazards in Original Scale
The hazard function for subject i is
![\[ h(t|\mb{x}_ i;\btheta )= h_0(t) \exp (\bbeta ’\mb{x}_ i) \]](images/statug_phreg0780.png)
where
![\[ h_0(t)= \lambda _ j ~ ~ \mr{if}~ a_{j-1} \le t < a_ j, j=1,\ldots ,J \]](images/statug_phreg0781.png)
The baseline cumulative hazard function is
![\[ H_0(t)= \sum _{j=1}^ J \lambda _ j \Delta _ j(t) \]](images/statug_phreg0782.png)
where
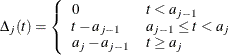
The log likelihood is given by
![\begin{eqnarray*} l(\blambda ,\bbeta ) & =& \sum _{i=1}^ n \delta _ i \biggl [ \sum _{j=1}^ J I(a_{j-1} \le t_ i <a_ j) \log \lambda _ j + \bbeta ’\mb{x}_ i \biggr ] - \sum _{i=1}^ n \biggl [ \sum _{j=1}^ J \Delta _ j(t_ i)\lambda _ j \biggr ] \exp (\bbeta ’\mb{x}_ i) \\ & =& \sum _{j=1}^ J d_ j \log \lambda _ j + \sum _{i=1}^ n \delta _ i \bbeta ’\mb{x}_ i -\sum _{j=1}^ J \lambda _ j \biggl [ \sum _{i=1}^ n \Delta _ j(t_ i)\exp (\bbeta ’\mb{x}_ i) \biggr ] \end{eqnarray*}](images/statug_phreg0784.png)
where 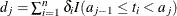 .
.
Note that for 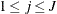 , the full conditional for
, the full conditional for 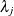 is log-concave only when
is log-concave only when 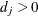 , but the full conditionals for the
, but the full conditionals for the 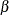 ’s are always log-concave.
’s are always log-concave.
For a given 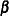 ,
, 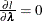 gives
gives
![\[ \tilde{\lambda }_ j(\bbeta )= \frac{d_ j}{\sum _{i=1}^ n\Delta _ j(t_ i) \exp (\bbeta '\mb{x}_ i)}, ~ ~ j=1,\ldots ,J \]](images/statug_phreg0790.png)
Substituting these values into 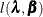 gives the profile log likelihood for
gives the profile log likelihood for 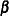
![\[ l_ p(\bbeta )= \sum _{i=1}^ n \delta _ i\bbeta ’\mb{x}_ i - \sum _{j=1}^ J d_ j \log \biggl [\sum _{l=1}^ n \Delta _ j(t_ l) \exp (\bbeta ’\mb{x}_ l) \biggr ] + c \]](images/statug_phreg0792.png)
where 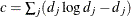 . Since the constant c does not depend on
. Since the constant c does not depend on 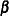 , it can be discarded from
, it can be discarded from 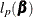 in the optimization.
in the optimization.
The MLE 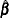 of
of 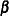 is obtained by maximizing
is obtained by maximizing
![\[ l_ p(\bbeta )= \sum _{i=1}^ n \delta _ i\bbeta ’\mb{x}_ i - \sum _{j=1}^ J d_ j \log \biggl [\sum _{l=1}^ n \Delta _ j(t_ l) \exp (\bbeta ’\mb{x}_ l) \biggr ] \]](images/statug_phreg0795.png)
with respect to 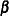 , and the MLE
, and the MLE 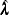 of
of 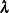 is given by
is given by
![\[ \hat{\blambda }=\tilde{\blambda }(\hat{\bbeta }) \]](images/statug_phreg0798.png)
For 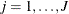 , let
, let
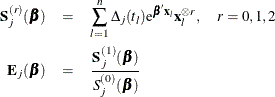
The partial derivatives of 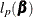 are
are
![\begin{eqnarray*} \frac{\partial l_ p(\bbeta )}{\partial \bbeta } & =& \sum _{i=1}^ n \delta _ i \mb{x}_ i - \sum _{j=1}^ J d_ j \bE _ j(\bbeta )\\ - \frac{\partial ^2 l_ p(\bbeta )}{\partial \bbeta ^2} & =& \sum _{j=1}^ J d_ j \biggl \{ \frac{\bS _ j^{(2)}(\bbeta )}{S_ j^{(0)}(\bbeta )} - \biggl [\bE _ j(\bbeta )\biggl ] \biggl [ \bE _ j(\bbeta )\biggr ]’\biggl \} \\ \end{eqnarray*}](images/statug_phreg0801.png)
The asymptotic covariance matrix for 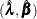 is obtained as the inverse of the information matrix given by
is obtained as the inverse of the information matrix given by
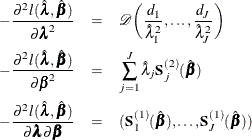
See Example 6.5.1 in Lawless (2003) for details.
Hazards in Log Scale
By letting
![\[ \alpha _ j=\log (\lambda _ j), \mbox{~ ~ } j=1,\ldots ,J \]](images/statug_phreg0804.png)
you can build a prior correlation among the 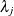 ’s by using a correlated prior
’s by using a correlated prior 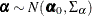 , where
, where 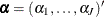 .
.
The log likelihood is given by
![\[ l(\balpha ,\bbeta ) = \sum _{j=1}^ J d_ j \alpha _ j + \sum _{i=1}^ n \delta _ i \bbeta ’\mb{x}_ i -\sum _{j=1}^ J \mr{e}^{\alpha _ j} S_ j^{(0)}(\bbeta ) \]](images/statug_phreg0807.png)
Then the MLE of 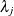 is given by
is given by
![\[ \mr{e}^{\hat{\alpha }_ j} = \hat{\lambda }_ j = \frac{d_ j}{S_ j^{0}(\hat{\bbeta })} \]](images/statug_phreg0808.png)
Note that the full conditionals for  ’s and
’s and 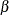 ’s are always log-concave.
’s are always log-concave.
The asymptotic covariance matrix for 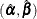 is obtained as the inverse of the information matrix formed by
is obtained as the inverse of the information matrix formed by
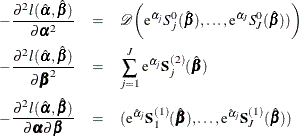
Counting Process Style of Input
Let ![$\{ ((s_ i,t_ i],\mb{x}_ i,\delta _ i), i=1,2,\ldots ,n\} $](images/statug_phreg0811.png) be the observed data. Let
be the observed data. Let 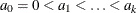 be a partition of the time axis, where
be a partition of the time axis, where 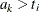 for all
for all 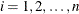 .
.
Replacing 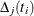 with
with
![\begin{eqnarray*} \Delta _ j((s_ i,t_ i]) = \left\{ \begin{array}{ll} 0 & t_ i<a_{j-1} \vee s_ i> a_ j \\ t_ i-\max (s_ i,a_{j-1}) & a_{j-1}\le t_ i < a_ j \\ a_ j - \max (s_ i,a_{j-1}) & t_ i \ge a_ j \end{array} \right. \end{eqnarray*}](images/statug_phreg0816.png)
the formulation for the single failure time variable applies.
Priors for Model Parameters
For a Cox model, the model parameters are the regression coefficients. For a piecewise exponential model, the model parameters consist of the regression coefficients and the hazards or log-hazards. The priors for the hazards and the priors for the regression coefficients are assumed to be independent, while you can have a joint multivariate normal prior for the log-hazards and the regression coefficients.
Hazard Parameters
Let  be the constant baseline hazards.
be the constant baseline hazards.
Improper Prior
The joint prior density is given by
![\[ p(\lambda _1,\ldots ,\lambda _ J) = \prod _{j=1}^ J \frac{1}{\lambda _ j}. \forall \lambda _ j > 0 \]](images/statug_phreg0817.png)
This prior is improper (nonintegrable), but the posterior distribution is proper as long as there is at least one event time in each of the constant hazard intervals.
Uniform Prior
The joint prior density is given by
![\[ p(\lambda _1,\ldots ,\lambda _ J) \propto 1, \forall \lambda _ j > 0 \]](images/statug_phreg0818.png)
This prior is improper (nonintegrable), but the posteriors are proper as long as there is at least one event time in each of the constant hazard intervals.
Gamma Prior
The gamma distribution 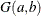 has a PDF
has a PDF
![\[ f_{a,b}(t) = \frac{b (b t)^{a-1}\mr{e}^{-b t}}{\Gamma (a)}, t>0 \]](images/statug_phreg0819.png)
where a is the shape parameter and 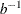 is the scale parameter. The mean is
is the scale parameter. The mean is 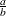 and the variance is
and the variance is 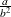 .
.
Independent Gamma Prior
Suppose for 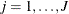 ,
, 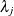 has an independent
has an independent 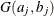 prior. The joint prior density is given by
prior. The joint prior density is given by
![\[ p(\lambda _1,\ldots ,\lambda _ J) \propto \prod _{j=1}^ J \biggl \{ \lambda _ j^{a_ j-1} \mr{e}^{-b_ j \lambda _ j} \biggr \} , \forall \lambda _ j > 0 \]](images/statug_phreg0824.png)
AR1 Prior
 are correlated as follows:
are correlated as follows:
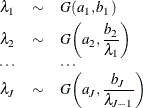
The joint prior density is given by
![\[ p(\lambda _1,\ldots ,\lambda _ J) \propto \lambda _1^{a_1 -1} \mr{e}^{-b_1 \lambda _1} \prod _{j=2}^ J \biggl (\frac{b_ j}{\lambda _{j-1}} \biggr )^{a_ j} \lambda _ j^{a_ j-1} \mr{e}^{- \frac{b_ j}{\lambda _{j-1}} \lambda _ j} \]](images/statug_phreg0827.png)
Log-Hazard Parameters
Write 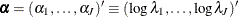 .
.
Uniform Prior
The joint prior density is given by
![\[ p(\alpha _1 \ldots \alpha _ J) \propto 1, \forall -\infty <\alpha _ i<\infty \]](images/statug_phreg0829.png)
Note that the uniform prior for the log-hazards is the same as the improper prior for the hazards.
Normal Prior
Assume  has a multivariate normal prior with mean vector
has a multivariate normal prior with mean vector 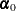 and covariance matrix
and covariance matrix 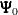 . The joint prior density is given by
. The joint prior density is given by
![\[ p(\balpha ) \propto \mr{e}^{-\frac{1}{2} (\balpha -\balpha _0)'\bPsi _0^{-1}(\balpha -\balpha _0)} \]](images/statug_phreg0833.png)
Regression Coefficients
Let 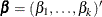 be the vector of regression coefficients.
be the vector of regression coefficients.
Uniform Prior
The joint prior density is given by
![\[ p(\beta _1,\ldots ,\beta _ k) \propto 1, \forall -\infty <\beta _ i<\infty \]](images/statug_phreg0834.png)
This prior is improper, but the posterior distributions for 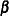 are proper.
are proper.
Normal Prior
Assume 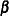 has a multivariate normal prior with mean vector
has a multivariate normal prior with mean vector 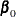 and covariance matrix
and covariance matrix 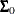 . The joint prior density is given by
. The joint prior density is given by
![\[ p(\bbeta ) \propto \mr{e}^{-\frac{1}{2} (\bbeta -\bbeta _0)'\bSigma _0^{-1}(\bbeta -\bbeta _0)} \]](images/statug_phreg0837.png)
Joint Multivariate Normal Prior for Log-Hazards and Regression Coefficients
Assume 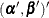 has a multivariate normal prior with mean vector
has a multivariate normal prior with mean vector 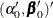 and covariance matrix
and covariance matrix 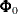 . The joint prior density is given by
. The joint prior density is given by
![\[ p(\balpha ,\bbeta ) \propto \mr{e}^{-\frac{1}{2} [(\balpha -\balpha _0)',(\bbeta -\bbeta _0)']\bPhi _0^{-1} [(\balpha -\balpha _0)',(\bbeta -\bbeta _0)']'} \]](images/statug_phreg0841.png)
Zellner’s g-Prior
Assume 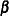 has a multivariate normal prior with mean vector
has a multivariate normal prior with mean vector 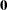 and covariance matrix
and covariance matrix 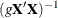 , where
, where 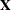 is the design matrix and g is either a constant or it follows a gamma prior with density
is the design matrix and g is either a constant or it follows a gamma prior with density 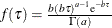 where a and b are the SHAPE= and ISCALE= parameters. Let k be the rank of
where a and b are the SHAPE= and ISCALE= parameters. Let k be the rank of 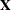 . The joint prior density with g being a constant c is given by
. The joint prior density with g being a constant c is given by
![\[ p(\bbeta ) \propto c^{\frac{k}{2}} \mr{e}^{-\frac{1}{2} \bbeta '(c\bX ^\prime \bX )^{-1}\bbeta } \\ \]](images/statug_phreg0844.png)
The joint prior density with g having a gamma prior is given by
![\[ p(\bbeta ,\tau ) \propto \tau ^{\frac{k}{2}} \mr{e}^{-\frac{1}{2} \bbeta '(\tau \bX ^\prime \bX )^{-1}\bbeta } \frac{b(b\tau )^{a-1}{\mr{e}}^{-b\tau }}{\Gamma (a)} \]](images/statug_phreg0845.png)
Dispersion Parameter for Frailty Model
Improper Prior
The density is
![\[ p(\theta )= \frac{1}{\theta } \]](images/statug_phreg0846.png)
Inverse Gamma Prior
The inverse gamma distribution 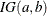 has a density
has a density
![\[ p(\theta |a,b)=\frac{b^ a \theta ^{-(a+1)} \mr{e}^{-\frac{b}{\theta }}}{\Gamma (a)} \]](images/statug_phreg0847.png)
where a and b are the SHAPE= and SCALE= parameters.
Gamma Prior
The gamma distribution 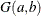 has a density
has a density
![\[ p(\theta |a,b)= \frac{b^ a \theta ^{a-1}\mr{e}^{-b\theta }}{\Gamma (a)} \]](images/statug_phreg0848.png)
where a and b are the SHAPE= and ISCALE= parameters.
Posterior Distribution
Denote the observed data by D.
Cox Model
![\[ \pi (\bbeta |D) \propto \underbrace{L_(D|\bbeta )}_{\mr{partial~ likelihood}} \overbrace{p(\bbeta )}^{\mr{prior}} \]](images/statug_phreg0849.png)
Frailty Model
Based on the framework of Sargent (1998),
![\[ \pi (\bbeta ,\bgamma ,\theta |D) \propto \underbrace{L(D|\bbeta ,\bgamma )}_{\mr{partial~ likelihood}} \overbrace{g(\bgamma |\theta )}^{\mr{random~ effects}} \underbrace{p(\bbeta ) p(\theta )}_{\mr{priors}} \]](images/statug_phreg0850.png)
where the joint density of the random effects 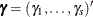 is given by
is given by
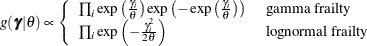
Piecewise Exponential Model
Hazard Parameters
![\[ \pi (\blambda ,\bbeta |D) \propto L_ H(D|\blambda ,\bbeta ) p(\blambda ) p(\bbeta ) \]](images/statug_phreg0852.png)
where 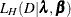 is the likelihood function with hazards
is the likelihood function with hazards 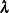 and regression coefficients
and regression coefficients 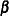 as parameters.
as parameters.
Log-Hazard Parameters
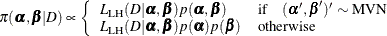
where 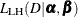 is the likelihood function with log-hazards
is the likelihood function with log-hazards  and regression coefficients
and regression coefficients 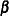 as parameters.
as parameters.
Sampling from the Posterior Distribution
For the Gibbs sampler, PROC PHREG uses the ARMS (adaptive rejection Metropolis sampling) algorithm of Gilks, Best, and Tan (1995) to sample from the full conditionals. This is the default sampling scheme. Alternatively, you can requests the random walk Metropolis (RWM) algorithm to sample an entire parameter vector from the posterior distribution. For a general discussion of these algorithms, see section Markov Chain Monte Carlo Method in Chapter 7: Introduction to Bayesian Analysis Procedures.
You can output these posterior samples into a SAS data set by using the OUTPOST= option in the BAYES statement, or you can
use the following SAS statement to output the posterior samples into the SAS data set Post:
ods output PosteriorSample=Post;
The output data set also includes the variables LogLike and LogPost, which represent the log of the likelihood and the log of the posterior log density, respectively.
Let 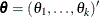 be the parameter vector. For the Cox model, the
be the parameter vector. For the Cox model, the 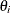 ’s are the regression coefficients
’s are the regression coefficients 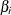 ’s, and for the piecewise constant baseline hazard model, the
’s, and for the piecewise constant baseline hazard model, the 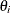 ’s consist of the baseline hazards
’s consist of the baseline hazards 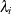 ’s (or log baseline hazards
’s (or log baseline hazards 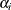 ’s) and the regression coefficients
’s) and the regression coefficients 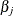 ’s. Let
’s. Let 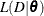 be the likelihood function, where D is the observed data. Note that for the Cox model, the likelihood contains the infinite-dimensional baseline hazard function,
and the gamma process is perhaps the most commonly used prior process (Ibrahim, Chen, and Sinha 2001). However, Sinha, Ibrahim, and Chen (2003) justify using the partial likelihood as the likelihood function for the Bayesian analysis. Let
be the likelihood function, where D is the observed data. Note that for the Cox model, the likelihood contains the infinite-dimensional baseline hazard function,
and the gamma process is perhaps the most commonly used prior process (Ibrahim, Chen, and Sinha 2001). However, Sinha, Ibrahim, and Chen (2003) justify using the partial likelihood as the likelihood function for the Bayesian analysis. Let 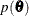 be the prior distribution. The posterior
be the prior distribution. The posterior 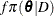 is proportional to the joint distribution
is proportional to the joint distribution 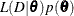 .
.
Gibbs Sampler
The full conditional distribution of 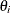 is proportional to the joint distribution; that is,
is proportional to the joint distribution; that is,
![\[ \pi (\theta _ i | \theta _ j, i \neq j, D) \propto L(D|\btheta ) p(\btheta ) \]](images/statug_phreg0864.png)
For example, the one-dimensional conditional distribution of 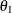 , given
, given 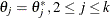 , is computed as
, is computed as
![\[ \pi (\theta _1 | \theta _ j=\theta _ j^*, 2\leq j \leq k, D) = L(D|\btheta =(\theta _1, \theta ^*_2,\ldots ,\theta ^*_ k)’) p(\btheta =(\theta _1, \theta ^*_2,\ldots ,\theta ^*_ k)’) \]](images/statug_phreg0867.png)
Suppose you have a set of arbitrary starting values 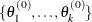 . Using the ARMS algorithm, an iteration of the Gibbs sampler consists of the following:
. Using the ARMS algorithm, an iteration of the Gibbs sampler consists of the following:
-
draw
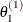 from
from 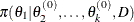
-
draw
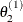 from
from 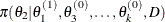
-

-
draw
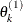 from
from 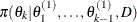
After one iteration, you have 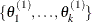 . After n iterations, you have
. After n iterations, you have 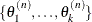 . Cumulatively, a chain of n samples is obtained.
. Cumulatively, a chain of n samples is obtained.
Random Walk Metropolis Algorithm
PROC PHREG uses a multivariate normal proposal distribution 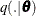 centered at
centered at 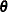 . With an initial parameter vector
. With an initial parameter vector 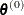 , a new sample
, a new sample 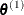 is obtained as follows:
is obtained as follows:
-
sample
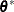 from
from 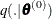
-
calculate the quantity
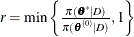
-
sample u from the uniform distribution
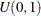
-
set
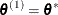 if
if 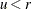 ; otherwise set
; otherwise set 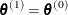
With 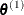 taking the role of
taking the role of 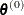 , the previous steps are repeated to generate the next sample
, the previous steps are repeated to generate the next sample 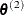 . After n iterations, a chain of n samples
. After n iterations, a chain of n samples  is obtained.
is obtained.
Starting Values of the Markov Chains
When the BAYES statement is specified, PROC PHREG generates one Markov chain that contains the approximate posterior samples
of the model parameters. Additional chains are produced when the Gelman-Rubin diagnostics are requested. Starting values (initial
values) can be specified in the INITIAL= data set in the BAYES statement. If the INITIAL= option is not specified, PROC PHREG
picks its own initial values for the chains based on the maximum likelihood estimates of 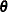 and the prior information of
and the prior information of 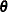 .
.
Denote ![$[x]$](images/statug_phreg0890.png) as the integral value of x.
as the integral value of x.
Constant Baseline Hazard Parameters 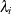 ’s
’s
For the first chain that the summary statistics and diagnostics are based on, the initial values are
![\[ \lambda _ i^{(0)} = \hat{\lambda }_ i \]](images/statug_phreg0891.png)
For subsequent chains, the starting values are picked in two different ways according to the total number of chains specified.
If the total number of chains specified is less than or equal to 10, initial values of the rth chain (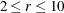 ) are given by
) are given by
![\[ \lambda _ i^{(0)} = \hat{\lambda }_ i \mr{e}^{\pm \biggl ([\frac{r}{2}]+2 \biggl ) \hat{s}(\hat{\lambda }_ i)} \]](images/statug_phreg0893.png)
with the plus sign for odd r and minus sign for even r. If the total number of chains is greater than 10, initial values are picked at random over a wide range of values. Let 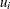 be a uniform random number between 0 and 1; the initial value for
be a uniform random number between 0 and 1; the initial value for 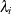 is given by
is given by
![\[ \lambda _ i^{(0)} = \hat{\lambda }_ i \mr{e}^{ 16(u_ i-0.5)\hat{s}(\hat{\lambda }_ i)} \]](images/statug_phreg0895.png)
Regression Coefficients and Log-Hazard Parameters 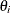 ’s
’s
The 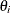 ’s are the regression coefficients
’s are the regression coefficients 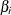 ’s, and in the piecewise exponential model, include the log-hazard parameters
’s, and in the piecewise exponential model, include the log-hazard parameters 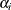 ’s. For the first chain that the summary statistics and regression diagnostics are based on, the initial values are
’s. For the first chain that the summary statistics and regression diagnostics are based on, the initial values are
![\[ \theta _ i^{(0)} = \hat{\theta }_ i \]](images/statug_phreg0896.png)
If the number of chains requested is less than or equal to 10, initial values for the rth chain (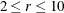 ) are given by
) are given by
![\[ \theta _ i^{(0)} = \hat{\theta }_ i \pm \biggl (2+ \biggl [\frac{r}{2} \biggr ] \biggr ) \hat{s}(\hat{\theta }_ i) \]](images/statug_phreg0898.png)
with the plus sign for odd r and minus sign for even r. When there are more than 10 chains, the initial value for the 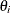 is picked at random over the range
is picked at random over the range 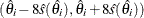 ; that is,
; that is,
![\[ \theta _ i^{(0)} = \hat{\theta }_ i + 16(u_ i-0.5)\hat{s}(\hat{\theta }_ i) \]](images/statug_phreg0900.png)
where 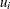 is a uniform random number between 0 and 1.
is a uniform random number between 0 and 1.
Fit Statistics
Denote the observed data by D. Let 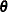 be the vector of parameters of length k. Let
be the vector of parameters of length k. Let 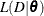 be the likelihood. The deviance information criterion (DIC) proposed in Spiegelhalter et al. (2002) is a Bayesian model assessment tool. Let Dev
be the likelihood. The deviance information criterion (DIC) proposed in Spiegelhalter et al. (2002) is a Bayesian model assessment tool. Let Dev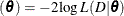 . Let
. Let 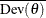 and
and 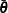 be the corresponding posterior means of
be the corresponding posterior means of 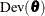 and
and 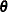 , respectively. The deviance information criterion is computed as
, respectively. The deviance information criterion is computed as
![\[ \mr{DIC} = 2\overline{\mr{Dev}(\btheta )} - \mr{Dev}(\bar{\btheta }) \]](images/statug_phreg0905.png)
Also computed is
![\[ pD= \overline{\mr{Dev}(\btheta )} - \mr{Dev}(\bar{\btheta }) \]](images/statug_phreg0906.png)
where pD is interpreted as the effective number of parameters.
Note that 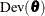 defined here does not have the standardizing term as in the section Deviance Information Criterion (DIC) in Chapter 7: Introduction to Bayesian Analysis Procedures. Nevertheless, the DIC calculated here is still useful for variable selection.
defined here does not have the standardizing term as in the section Deviance Information Criterion (DIC) in Chapter 7: Introduction to Bayesian Analysis Procedures. Nevertheless, the DIC calculated here is still useful for variable selection.
Posterior Distribution for Quantities of Interest
Let 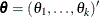 be the parameter vector. For the Cox model, the
be the parameter vector. For the Cox model, the 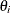 ’s are the regression coefficients
’s are the regression coefficients 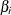 ’s; for the piecewise constant baseline hazard model, the
’s; for the piecewise constant baseline hazard model, the 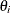 ’s consist of the baseline hazards
’s consist of the baseline hazards 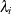 ’s (or log baseline hazards
’s (or log baseline hazards 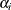 ’s) and the regression coefficients
’s) and the regression coefficients 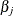 ’s. Let
’s. Let 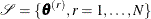 be the chain that represents the posterior distribution for
be the chain that represents the posterior distribution for 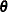 .
.
Consider a quantity of interest  that can be expressed as a function
that can be expressed as a function 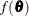 of the parameter vector
of the parameter vector 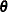 . You can construct the posterior distribution of
. You can construct the posterior distribution of  by evaluating the function
by evaluating the function 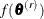 for each
for each 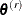 in
in 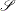 . The posterior chain for
. The posterior chain for  is
is 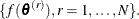 Summary statistics such as mean, standard deviation, percentiles, and credible intervals are used to describe the posterior
distribution of
Summary statistics such as mean, standard deviation, percentiles, and credible intervals are used to describe the posterior
distribution of  .
.
Hazard Ratio
As shown in the section Hazard Ratios, a log-hazard ratio is a linear combination of the regression coefficients. Let 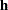 be the vector of linear coefficients. The posterior sample for this hazard ratio is the set
be the vector of linear coefficients. The posterior sample for this hazard ratio is the set 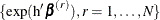 .
.
Survival Distribution
Let  be a covariate vector of interest.
be a covariate vector of interest.
Cox Model
Let 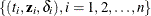 be the observed data. Define
be the observed data. Define
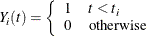
Consider the rth draw 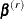 of
of 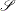 . The baseline cumulative hazard function at time t is given by
. The baseline cumulative hazard function at time t is given by
![\[ H_0(t|\bbeta ^{(r)}) = \sum _{i:t_ i\leq t} \frac{\delta _ i}{\sum _{l=1}^ n Y_ l(t_ i)\mr{exp}(\mb{z}'_ l \bbeta ^{(r)})} \]](images/statug_phreg0918.png)
For the given covariate vector  , the cumulative hazard function at time t is
, the cumulative hazard function at time t is
![\[ H(t;\mb{x}|\bbeta ^{(r)}) = H_0(t|\bbeta ^{(r)})\exp (\mb{x}’\bbeta ^{(r)}) \]](images/statug_phreg0919.png)
and the survival function at time t is
![\[ S(t;\mb{x}|\bbeta ^{(r)}) = \exp [-H^{(r)}(t;\mb{x}|\bbeta ^{(r)})] \]](images/statug_phreg0920.png)
Piecewise Exponential Model
Let 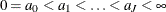 be a partition of the time axis. Consider the rth draw
be a partition of the time axis. Consider the rth draw 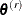 in
in 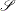 , where
, where 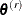 consists of
consists of 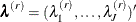 and
and 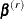 . The baseline cumulative hazard function at time t is
. The baseline cumulative hazard function at time t is
![\[ H_0(t|\blambda ^{(r)})= \sum _{j=1}^ J \lambda ^{(r)}_ j \Delta _ j(t) \]](images/statug_phreg0923.png)
where
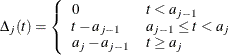
For the given covariate vector  , the cumulative hazard function at time t is
, the cumulative hazard function at time t is
![\[ H(t;\mb{x}|\blambda ^{(r)},\bbeta ^{(r)})=H_0(t|\blambda ^{(r)})\exp (\mb{x}’\bbeta ^{(r)}) \]](images/statug_phreg0925.png)
and the survival function at time t is
![\[ S(t;\mb{x}|\blambda ^{(r)},\bbeta ^{(r)}) = \exp [-H(t;\mb{x}|\blambda ^{(r)},\bbeta ^{(r)})] \]](images/statug_phreg0926.png)