The PHREG Procedure

Proportional Rates/Means Models for Recurrent Events

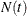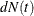Let $N(t)$ be the number of events experienced by a subject over the time interval $(0,t]$. Let $dN(t)$ be the increment of the counting process N over 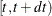$[t,t+dt)$. The rate function is given by

\[ d\mu _{\bZ }(t)= E[dN(t) | Z(t)] = \mr{e}^{\bbeta '\bZ (t)}d\mu _0(t) \]

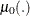where $\mu _0(.)$ is an unknown continuous function. If the 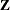$\bZ $ are time independent, the rate model is reduced to the mean model

\[ \mu _ Z(t)= \mr{e}^{\bbeta 'Z} \mu _0(t) \]

The partial likelihood for n independent triplets 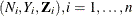$(N_{i},Y_{i},\mb{Z}_{i}), i=1, \ldots , n$, of counting, at-risk, and covariate processes is the same as that of the multiplicative hazards model. However, a robust sandwich estimate is used for the covariance matrix of the parameter estimator instead of the model-based estimate.

Let 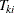$T_{ki}$ be the kth event time of the ith subject. Let 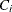$C_ i$ be the censoring time of the ith subject. The at-risk indicator and the failure indicator are, respectively,

\[ Y_ i(t) = I(C_ i\ge t) ~ ~ \mr{and}~ ~ \Delta _{ki}= I(T_{ki} \le C_ i) \]

Denote

\[ S^{(0)}(\bbeta ,t) = \sum _{i=1}^ n Y_ i(t)\mr{e}^{\bbeta '\bZ _ i(t)} ~ ~ \mr{and}~ ~ \bar{\bZ }(\bbeta ,t) = \frac{\sum _{i=1}^ n Y_ i(t)\mr{e}^{\bbeta '\bZ _ i(t)} \bZ _ i(t)}{S^{(0)}(\bbeta ,t)} \]

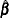Let $\hat{\bbeta }$ be the maximum likelihood estimate of 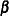$\bbeta $, and let 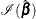$\mc{I}(\hat{\bbeta })$ be the observed information matrix. The robust sandwich covariance matrix estimate is given by

\[ \mc{I}^{-1}(\hat{\bbeta })\sum _{i=1}^ n \biggl [ W_ i(\hat{\bbeta }) W’_ i(\hat{\bbeta }) \biggl ] \mc{I}^{-1}(\hat{\bbeta }) \]

where

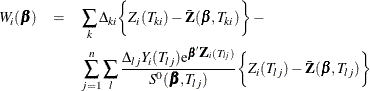
\begin{eqnarray*} W_ i(\bbeta ) & =& \sum _ k \Delta _{ki}\biggl \{ Z_ i(T_{ki}) - \bar{\bZ }(\bbeta ,T_{ki}) \biggr \} - \\ & & \sum _{j=1}^ n \sum _ l \frac{\Delta _{lj}Y_ i(T_{lj}) \mr{e}^{\bbeta '\bZ _ i(T_{lj})}}{S^{0}(\bbeta ,T_{lj}) } \biggl \{ Z_ i(T_{lj}) - \bar{\bZ }(\bbeta ,T_{lj}) \biggr \} \end{eqnarray*}

For a given realization of the covariates 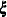$\bxi $, the Nelson estimator is used to predict the mean function

\[ \hat{\mu }_{\bxi }(t) = \mr{e}^{\hat{\bbeta }'\bxi } \sum _{i=1}^ n \sum _ k \frac{I(T_{ki} \le t) \Delta _{ki}}{S^{(0)}(\hat{\bbeta },T_{ki})} \]

with standard error estimate given by

\[ \hat{\sigma }^2(\hat{\mu }_{\bxi }(t)) = \sum _{i=1}^ n \biggl (\frac{1}{n}\hat{\Psi }_ i(t,\bxi ) \biggr )^2 \]

where

\begin{eqnarray*} \frac{1}{n}\hat{\Psi }_ i(t,\bxi ) & = & \mr{e}^{\hat{\bbeta }'\bxi } \biggl \{ \sum _ k \frac{I(T_{ki}\le t)\Delta _{ki}}{S^{(0)}(\hat{\bbeta },T_{ki})} - \sum _{j=1}^ n\sum _ k \frac{Y_ i(T_{kj}) \mr{e}^{\hat{\bbeta }'\bZ _ i(T_{kj})}I(T_{kj} \le t)\Delta _{kj}}{[S^{(0)}(\hat{\bbeta },T_{kj})]^2} - \\ & & \biggl [ \sum _{i=1}^ n \sum _ k \frac{I(T_{ki}\le t)\Delta _{ki} [\bar{\bZ }(\hat{\bbeta },T_{ki}) - \bxi ]}{S^{(0)}(\hat{\bbeta },T_{ki})} \biggr ] \\ & & \times \mc{I}^{-1}(\hat{\bbeta })\int _0^{\tau } [\bZ _ i(u) - \bar{\bZ }(\hat{\bbeta },u)]d\hat{M}_ i(u)\biggl \} \end{eqnarray*}

Since the cumulative mean function is always nonnegative, the log transform is used to compute confidence intervals. The 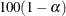$100(1-\alpha )$% pointwise confidence limits for 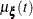$ \mu _{\bxi }(t)$ are

\[ \hat{\mu }_{\bxi }(t) \mr{e}^{\pm z_{\alpha /2} \frac{\hat{\sigma }(\hat{\mu }_{\bxi }(t)) }{\hat{\mu }{\bxi }(t)}} \]

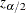where $z_{\alpha /2}$ is the upper 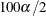$100\alpha /2$ percentage point of the standard normal distribution.