The PHREG Procedure

Confidence Limits for a Hazard Ratio

Subsections:

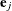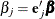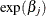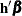Let $\mb{e}_ j$ be the jth unit vector—that is, the jth entry of the vector is 1 and all other entries are 0. The hazard ratio for the explanatory variable with regression coefficient $\beta _ j=\mb{e}_ j’\bbeta $ is defined as $\textrm{exp}(\beta _ j)$. In general, a log-hazard ratio can be written as $\mb{h}’\bbeta $, a linear combination of the regression coefficients, and the hazard ratio 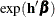$\textrm{exp}({\mb{h}’\bbeta })$ is obtained by replacing 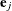$\mb{e}_ j$ with $\mb{h}$.

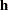Point Estimate

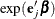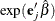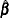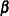The hazard ratio $\textrm{exp}(\mb{e}_ j’\bbeta )$ is estimated by $\textrm{exp}(\mb{e}_ j’\hat{\beta })$, where $\hat{\bbeta }$ is the maximum likelihood estimate of the $\bbeta $.

Wald’s Confidence Limits

The 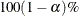$100(1-{\alpha })\% $ confidence limits for the hazard ratio are calculated as

\[ \mr{exp} \left(\mb{e}_ j’ \hat{\beta } \pm z_{\alpha /2} \sqrt {\mb{e}_ j’\hat{\mb{V}}(\hat{\bbeta })\mb{e}_ j} \right) \]

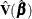where $\hat{\bV }(\hat{\bbeta })$ is estimated covariance matrix, and 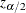$z_{\alpha /2}$ is the 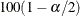$100(1-\alpha /2)$th percentile point of the standard normal distribution.

Profile-Likelihood Confidence Limits

The construction of the profile-likelihood-based confidence interval is derived from the asymptotic 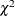$\chi ^2$ distribution of the generalized likelihood ratio test of Venzon and Moolgavkar (1988). Suppose that the parameter vector is 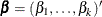$\bbeta = (\beta _{1},\ldots ,\beta _{k})’$ and you want to compute a confidence interval for 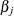$\beta _{j}$. The profile-likelihood function for 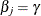$\beta _{j}=\gamma $ is defined as

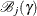\[ l_ j^*(\gamma ) = \max _{\bbeta \in \mc{B}_ j(\gamma )} l(\bbeta ) \]

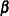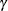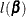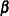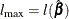where $\mc{B}_ j(\gamma )$ is the set of all $\bbeta $ with the jth element fixed at $\gamma $, and $l(\bbeta )$ is the log-likelihood function for $\bbeta $. If $l_{\max } = l(\hat{\bbeta })$ is the log likelihood evaluated at the maximum likelihood estimate 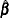$\hat{\bbeta }$, then 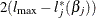$ 2( l_{\max } - l_ j^{*}(\beta _{j} )) $ has a limiting chi-square distribution with one degree of freedom if 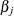$\beta _{j}$ is the true parameter value. Let 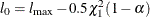$l_0=l_{\max } -0.5\chi ^{2}_{1}(1-\alpha )$, where 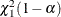$\chi ^{2}_{1}(1-\alpha )$ is the 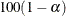$100(1-\alpha )$th percentile of the chi-square distribution with one degree of freedom. A 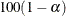$100(1-\alpha )$% confidence interval for 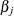$\beta _{j}$ is

\[ \{ \gamma : l_ j^*(\gamma ) \geq l_{0} \} \]

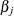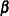The endpoints of the confidence interval are found by solving numerically for values of $\beta _{j}$ that satisfy equality in the preceding relation. To obtain an iterative algorithm for computing the confidence limits, the log-likelihood function in a neighborhood of $\bbeta $ is approximated by the quadratic function

\[ \tilde{l}(\bbeta + \bdelta ) = l(\bbeta ) + \bdelta ’\mb{g} + \frac{1}{2}\bdelta ’ \mb{V} \bdelta \]

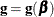where $\mb{g}=\mb{g}(\bbeta )$ is the gradient vector and 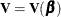$\bV =\bV (\bbeta )$ is the Hessian matrix. The increment 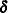$\bdelta $ for the next iteration is obtained by solving the likelihood equations

\[ \frac{d}{d\bdelta }\{ \tilde{l}(\bbeta + \bdelta ) + \lambda ( \mb{e}_ j’\bdelta - \gamma )\} = \mb{0} \]

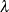where $\lambda $ is the Lagrange multiplier, 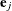$\mb{e}_ j$ is the jth unit vector, and 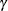$\gamma $ is an unknown constant. The solution is

\[ \bdelta = -\mb{V}^{-1}(\mb{g} + \lambda \mb{e}_ j) \]

By substituting this 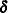$\bdelta $ into the equation 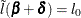$\tilde{l}(\bbeta + \bdelta ) = l_0$, you can estimate 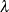$\lambda $ as

\[ \lambda = \pm \biggl (\frac{2(l_0 - l(\bbeta ) + \frac{1}{2}\mb{g}'\mb{V}^{-1}\mb{g})}{\mb{e}_ j'\mb{V}^{-1}\mb{e}_ j}\biggr )^{ \frac{1}{2}} \]

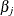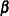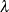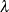The upper confidence limit for $\beta _ j$ is computed by starting at the maximum likelihood estimate of $\bbeta $ and iterating with positive values of $\lambda $ until convergence is attained. The process is repeated for the lower confidence limit, using negative values of $\lambda $.

Convergence is controlled by value $\epsilon $ specified with the PLCONV= option in the MODEL statement (the default value of $\epsilon $ is 1E–4). Convergence is declared on the current iteration if the following two conditions are satisfied:

\[ |l(\bbeta )-l_{0}| \leq \epsilon \]

and

\[ ({\mb{g}} + \lambda {\mb{e}_ j})’{\mb{V}}^{-1}(\mb{g} + \lambda {\mb{e}_ j}) \leq \epsilon \]

The profile-likelihood confidence limits for the hazard ratio 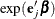$\textrm{exp}(\mb{e}_ j’\bbeta )$ are obtained by exponentiating these confidence limits.