The PHREG Procedure
- Overview
-
Getting Started

-
Syntax
 PROC PHREG StatementASSESS StatementBASELINE StatementBAYES StatementBY StatementCLASS StatementCONTRAST StatementEFFECT StatementESTIMATE StatementFREQ StatementHAZARDRATIO StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementProgramming StatementsRANDOM StatementSTRATA StatementSLICE StatementSTORE StatementTEST StatementWEIGHT Statement
PROC PHREG StatementASSESS StatementBASELINE StatementBAYES StatementBY StatementCLASS StatementCONTRAST StatementEFFECT StatementESTIMATE StatementFREQ StatementHAZARDRATIO StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementProgramming StatementsRANDOM StatementSTRATA StatementSLICE StatementSTORE StatementTEST StatementWEIGHT Statement -
Details
 Failure Time DistributionTime and CLASS Variables UsagePartial Likelihood Function for the Cox ModelCounting Process Style of InputLeft-Truncation of Failure TimesThe Multiplicative Hazards ModelProportional Rates/Means Models for Recurrent EventsThe Frailty ModelProportional Subdistribution Hazards Model for Competing-Risks DataHazard RatiosNewton-Raphson MethodFirth’s Modification for Maximum Likelihood EstimationRobust Sandwich Variance EstimateTesting the Global Null HypothesisType 3 Tests and Joint TestsConfidence Limits for a Hazard RatioUsing the TEST Statement to Test Linear HypothesesAnalysis of Multivariate Failure Time DataModel Fit StatisticsSchemper-Henderson Predictive MeasureResidualsDiagnostics Based on Weighted ResidualsInfluence of Observations on Overall Fit of the ModelSurvivor Function EstimatorsCaution about Using Survival Data with Left TruncationEffect Selection MethodsAssessment of the Proportional Hazards ModelThe Penalized Partial Likelihood Approach for Fitting Frailty ModelsSpecifics for Bayesian AnalysisComputational ResourcesInput and Output Data SetsDisplayed OutputODS Table NamesODS Graphics
Failure Time DistributionTime and CLASS Variables UsagePartial Likelihood Function for the Cox ModelCounting Process Style of InputLeft-Truncation of Failure TimesThe Multiplicative Hazards ModelProportional Rates/Means Models for Recurrent EventsThe Frailty ModelProportional Subdistribution Hazards Model for Competing-Risks DataHazard RatiosNewton-Raphson MethodFirth’s Modification for Maximum Likelihood EstimationRobust Sandwich Variance EstimateTesting the Global Null HypothesisType 3 Tests and Joint TestsConfidence Limits for a Hazard RatioUsing the TEST Statement to Test Linear HypothesesAnalysis of Multivariate Failure Time DataModel Fit StatisticsSchemper-Henderson Predictive MeasureResidualsDiagnostics Based on Weighted ResidualsInfluence of Observations on Overall Fit of the ModelSurvivor Function EstimatorsCaution about Using Survival Data with Left TruncationEffect Selection MethodsAssessment of the Proportional Hazards ModelThe Penalized Partial Likelihood Approach for Fitting Frailty ModelsSpecifics for Bayesian AnalysisComputational ResourcesInput and Output Data SetsDisplayed OutputODS Table NamesODS Graphics -
Examples
 Stepwise RegressionBest Subset SelectionModeling with Categorical PredictorsFirth’s Correction for Monotone LikelihoodConditional Logistic Regression for m:n MatchingModel Using Time-Dependent Explanatory VariablesTime-Dependent Repeated Measurements of a CovariateSurvival CurvesAnalysis of ResidualsAnalysis of Recurrent Events DataAnalysis of Clustered DataModel Assessment Using Cumulative Sums of Martingale ResidualsBayesian Analysis of the Cox ModelBayesian Analysis of Piecewise Exponential ModelAnalysis of Competing-Risks Data
Stepwise RegressionBest Subset SelectionModeling with Categorical PredictorsFirth’s Correction for Monotone LikelihoodConditional Logistic Regression for m:n MatchingModel Using Time-Dependent Explanatory VariablesTime-Dependent Repeated Measurements of a CovariateSurvival CurvesAnalysis of ResidualsAnalysis of Recurrent Events DataAnalysis of Clustered DataModel Assessment Using Cumulative Sums of Martingale ResidualsBayesian Analysis of the Cox ModelBayesian Analysis of Piecewise Exponential ModelAnalysis of Competing-Risks Data - References
Assessment of the Proportional Hazards Model
The proportional hazards model specifies that the hazard function for the failure time T associated with a 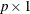 column covariate vector
column covariate vector 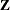 takes the form
takes the form
![\[ \lambda (t;\bZ )=\lambda _0(t)\mr{e}^{\bbeta '\bZ } \]](images/statug_phreg0707.png)
where 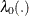 is an unspecified baseline hazard function and
is an unspecified baseline hazard function and 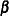 is a
is a 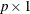 column vector of regression parameters. Lin, Wei, and Ying (1993) present graphical and numerical methods for model assessment based on the cumulative sums of martingale residuals and their
transforms over certain coordinates (such as covariate values or follow-up times). The distributions of these stochastic processes
under the assumed model can be approximated by the distributions of certain zero-mean Gaussian processes whose realizations
can be generated by simulation. Each observed residual pattern can then be compared, both graphically and numerically, with
a number of realizations from the null distribution. Such comparisons enable you to assess objectively whether the observed
residual pattern reflects anything beyond random fluctuation. These procedures are useful in determining appropriate functional
forms of covariates and assessing the proportional hazards assumption. You use the ASSESS statement to carry out these model-checking
procedures.
column vector of regression parameters. Lin, Wei, and Ying (1993) present graphical and numerical methods for model assessment based on the cumulative sums of martingale residuals and their
transforms over certain coordinates (such as covariate values or follow-up times). The distributions of these stochastic processes
under the assumed model can be approximated by the distributions of certain zero-mean Gaussian processes whose realizations
can be generated by simulation. Each observed residual pattern can then be compared, both graphically and numerically, with
a number of realizations from the null distribution. Such comparisons enable you to assess objectively whether the observed
residual pattern reflects anything beyond random fluctuation. These procedures are useful in determining appropriate functional
forms of covariates and assessing the proportional hazards assumption. You use the ASSESS statement to carry out these model-checking
procedures.
For a sample of n subjects, let 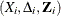 be the data of the ith subject; that is,
be the data of the ith subject; that is, 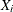 represents the observed failure time,
represents the observed failure time, 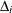 has a value of 1 if
has a value of 1 if 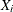 is an uncensored time and 0 otherwise, and
is an uncensored time and 0 otherwise, and 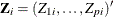 is a p-vector of covariates. Let
is a p-vector of covariates. Let 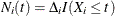 and
and 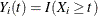 . Let
. Let
![\[ S^{(0)}(\bbeta ,t) = \sum _{i=1}^ n Y_ i(t)\mr{e}^{\bbeta '\bZ _ i} ~ ~ \mr{and}~ ~ \bZ (\bbeta ,t) = \frac{\sum _{i=1}^ n Y_ i(t)\mr{e}^{\bbeta '\bZ _ i}\bZ _ i}{S^{(0)}(\bbeta ,t)} \]](images/statug_phreg0713.png)
Let 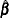 be the maximum partial likelihood estimate of
be the maximum partial likelihood estimate of 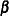 , and let
, and let 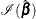 be the observed information matrix.
be the observed information matrix.
The martingale residuals are defined as
![\[ \hat{M}_ i(t) = N_ i(t) -\int _0^{t} Y_ i(u)\mr{e}^{\hat{\bbeta }'\bZ _ i} d\hat{\Lambda }_0(u), i=1,\ldots ,n \]](images/statug_phreg0714.png)
where 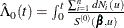 .
.
The empirical score process 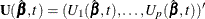 is a transform of the martingale residuals:
is a transform of the martingale residuals:
![\[ \bU (\hat{\bbeta },t) = \sum _{i=1}^ n \bZ _ i\hat{M}_ i(t) \]](images/statug_phreg0717.png)
Checking the Functional Form of a Covariate
To check the functional form of the jth covariate, consider the partial-sum process of
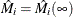 :
:
![\[ W_ j(z)= \sum _{i=1}^ n I(Z_{ji} \le z)\hat{M}_ i \]](images/statug_phreg0719.png)
Under that null hypothesis that the model holds, 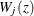 can be approximated by the zero-mean Gaussian process
can be approximated by the zero-mean Gaussian process
![\begin{eqnarray*} \hat{W}_{j}(z) & = & \sum _{l=1}^ n \Delta _ l \biggl \{ I(Z_{jl} \le z) - \frac{\sum _{i=1}^ n Y_ i(X_ l)\mr{e}^{\bbeta '\bZ _ i}I(Z_{ij}\le z)}{S^{(0)}(\hat{\bbeta },X_ l)}\biggr \} G_ l - \\ & & \sum _{k=1}^ n \int _0^\infty Y_ k(s) \mr{e}^{\hat{\bbeta }'\bZ _ k} I(Z_{jk} \le z) [\bZ _ k - \bar{\bZ }(\hat{\bbeta },s)]’d\hat{\Lambda }_0(s) \\ & & \times \mc{I}^{-1}(\hat{\bbeta }) \sum _{l=1}^ n \Delta _ l [\bZ _ l -\bar{\bZ }(\hat{\bbeta },X_ l) ] G_ l \\ \end{eqnarray*}](images/statug_phreg0721.png)
where 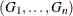 are independent standard normal variables that are independent of
are independent standard normal variables that are independent of 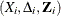 ,
, 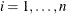 .
.
You can assess the functional form of the jth covariate by plotting a small number of realizations (the default is 20) of 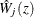 on the same graph as the observed
on the same graph as the observed 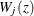 and visually comparing them to see how typical the observed pattern of
and visually comparing them to see how typical the observed pattern of 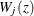 is of the null distribution samples. You can supplement the graphical inspection method with a Kolmogorov-type supremum test.
Let
is of the null distribution samples. You can supplement the graphical inspection method with a Kolmogorov-type supremum test.
Let 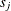 be the observed value of
be the observed value of 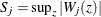 and let
and let 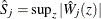 . The p-value
. The p-value 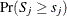 is approximated by
is approximated by 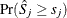 , which in turn is approximated by generating a large number of realizations (1000 is the default) of
, which in turn is approximated by generating a large number of realizations (1000 is the default) of 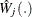 .
.
Checking the Proportional Hazards Assumption
Consider the standardized empirical score process
for the jth component of 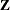
![\[ U_ j^*(t)=[\mc{I}^{-1}(\hat{\bbeta })_{jj}]^{\frac{1}{2}} U_ j(\hat{\bbeta },t), \]](images/statug_phreg0730.png)
Under the null hypothesis that the model holds, 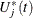 can be approximated by
can be approximated by
![\begin{eqnarray*} \hat{U}^*_ j(t) & =& [\mc{I}^{-1}(\hat{\bbeta })_{jj}]^{\frac{1}{2}} \biggl \{ \sum _{l=1}^ n I(X_ l\le t)\Delta _ l [Z_{jl} - \bar{Z_ j}(\hat{\bbeta },t)]G_ l - \\ & & \sum _{k=1}^ n \int _0^ t Y_ k(s)\mr{e}^{\hat{\bbeta }'\bZ _ k} Z_{jk} [ \bZ _ k - \bar{\bZ }(\hat{\bbeta },s) ]’d\hat{\Lambda }_0(s) \\ & & \times \mc{I}^{-1}(\hat{\bbeta }) \sum _{l=1}^ n \Delta _ l [\bZ _ l -\bar{\bZ }(\hat{\bbeta },X_ l)]G_ l \biggr \} \end{eqnarray*}](images/statug_phreg0732.png)
where 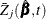 is the jth component of
is the jth component of 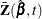 , and
, and 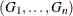 are independent standard normal variables that are independent of
are independent standard normal variables that are independent of 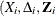 ,
, 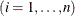 .
.
You can assess the proportional hazards assumption for the jth covariate by plotting a few realizations of 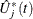 on the same graph as the observed
on the same graph as the observed 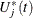 and visually comparing them to see how typical the observed pattern of
and visually comparing them to see how typical the observed pattern of 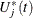 is of the null distribution samples. Again you can supplement the graphical inspection method with a Kolmogorov-type supremum
test. Let
is of the null distribution samples. Again you can supplement the graphical inspection method with a Kolmogorov-type supremum
test. Let 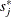 be the observed value of
be the observed value of 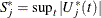 and let
and let 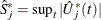 . The p-value
. The p-value ![$\mr{Pr}[S^*_ j \ge s^*_ j]$](images/statug_phreg0741.png) is approximated by
is approximated by ![$\mr{Pr}[\hat{S}^*_ j \ge s_ j^*]$](images/statug_phreg0742.png) , which in turn is approximated by generating a large number of realizations (1000 is the default) of
, which in turn is approximated by generating a large number of realizations (1000 is the default) of 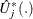 .
.