Introduction to Bayesian Analysis Procedures
Markov Chain Monte Carlo Method
The Markov chain Monte Carlo (MCMC) method is a general simulation method for sampling from posterior distributions and computing
posterior quantities of interest. MCMC methods sample successively from a target distribution. Each sample depends on the
previous one, hence the notion of the Markov chain. A Markov chain is a sequence of random variables, 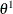 ,
, 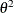 ,
,  , for which the random variable
, for which the random variable 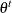 depends on all previous
depends on all previous 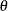 s only through its immediate predecessor
s only through its immediate predecessor 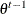 . You can think of a Markov chain applied to sampling as a mechanism that traverses randomly through a target distribution
without having any memory of where it has been. Where it moves next is entirely dependent on where it is now.
. You can think of a Markov chain applied to sampling as a mechanism that traverses randomly through a target distribution
without having any memory of where it has been. Where it moves next is entirely dependent on where it is now.
Monte Carlo, as in Monte Carlo integration, is mainly used to approximate an expectation by using the Markov chain samples. In the simplest version
![\[ \int _ S g(\theta ) p(\theta ) d\theta \cong \frac{1}{n} \sum _{t=1}^{n} g(\theta ^ t) \]](images/statug_introbayes0059.png)
where 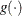 is a function of interest and
is a function of interest and 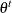 are samples from
are samples from 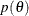 on its support S. This approximates the expected value of
on its support S. This approximates the expected value of 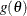 . The earliest reference to MCMC simulation occurs in the physics literature. Metropolis and Ulam (1949) and Metropolis et al. (1953) describe what is known as the Metropolis algorithm
(see the section Metropolis and Metropolis-Hastings Algorithms). The algorithm can be used to generate sequences of samples from the joint distribution of multiple variables, and it is
the foundation of MCMC. Hastings (1970) generalized their work, resulting in the Metropolis-Hastings algorithm.
Geman and Geman (1984) analyzed image data by using what is now called Gibbs sampling
(see the section Gibbs Sampler). These MCMC methods first appeared in the mainstream statistical literature in Tanner and Wong (1987).
. The earliest reference to MCMC simulation occurs in the physics literature. Metropolis and Ulam (1949) and Metropolis et al. (1953) describe what is known as the Metropolis algorithm
(see the section Metropolis and Metropolis-Hastings Algorithms). The algorithm can be used to generate sequences of samples from the joint distribution of multiple variables, and it is
the foundation of MCMC. Hastings (1970) generalized their work, resulting in the Metropolis-Hastings algorithm.
Geman and Geman (1984) analyzed image data by using what is now called Gibbs sampling
(see the section Gibbs Sampler). These MCMC methods first appeared in the mainstream statistical literature in Tanner and Wong (1987).
The Markov chain method has been quite successful in modern Bayesian computing. Only in the simplest Bayesian models can you
recognize the analytical forms of the posterior distributions and summarize inferences directly. In moderately complex models,
posterior densities are too difficult to work with directly. With the MCMC method, it is possible to generate samples from
an arbitrary posterior density 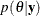 and to use these samples to approximate expectations of quantities of interest. Several other aspects of the Markov chain
method also contributed to its success. Most importantly, if the simulation algorithm is implemented correctly, the Markov
chain is guaranteed to converge to the target distribution
and to use these samples to approximate expectations of quantities of interest. Several other aspects of the Markov chain
method also contributed to its success. Most importantly, if the simulation algorithm is implemented correctly, the Markov
chain is guaranteed to converge to the target distribution 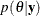 under rather broad conditions, regardless of where the chain was initialized. In other words, a Markov chain is able to improve
its approximation to the true distribution at each step in the simulation. Furthermore, if the chain is run for a very long
time (often required), you can recover
under rather broad conditions, regardless of where the chain was initialized. In other words, a Markov chain is able to improve
its approximation to the true distribution at each step in the simulation. Furthermore, if the chain is run for a very long
time (often required), you can recover 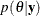 to any precision. Also, the simulation algorithm is easily extensible to models with a large number of parameters or high
complexity, although the "curse of dimensionality" often causes problems in practice.
to any precision. Also, the simulation algorithm is easily extensible to models with a large number of parameters or high
complexity, although the "curse of dimensionality" often causes problems in practice.
Properties of Markov chains are discussed in Feller (1968), Breiman (1968), and Meyn and Tweedie (1993). Ross (1997) and Karlin and Taylor (1975) give a non-measure-theoretic treatment of stochastic processes, including Markov chains. For conditions that govern Markov chain convergence and rates of convergence, see Amit (1991), Applegate, Kannan, and Polson (1990), Chan (1993), Geman and Geman (1984), Liu, Wong, and Kong (1991a, 1991b), Rosenthal (1991a, 1991b), Tierney (1994), and Schervish and Carlin (1992). Besag (1974) describes conditions under which a set of conditional distributions gives a unique joint distribution. Tanner (1993), Gilks, Richardson, and Spiegelhalter (1996), Chen, Shao, and Ibrahim (2000), Liu (2001), Gelman et al. (2004), Robert and Casella (2004), and Congdon (2001, 2003, 2005) provide both theoretical and applied treatments of MCMC methods. You can also see the section A Bayesian Reading List for a list of books with varying levels of difficulty of treatment of the subject and its application to Bayesian statistics.
Metropolis and Metropolis-Hastings Algorithms
The Metropolis algorithm is named after its inventor, the American physicist and computer scientist Nicholas C. Metropolis. The algorithm is simple but practical, and it can be used to obtain random samples from any arbitrarily complicated target distribution of any dimension that is known up to a normalizing constant.
Suppose you want to obtain T samples from a univariate distribution with probability density function 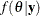 . Suppose
. Suppose 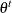 is the tth sample from f. To use the Metropolis algorithm, you need to have an initial value
is the tth sample from f. To use the Metropolis algorithm, you need to have an initial value 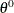 and a symmetric proposal density
and a symmetric proposal density 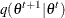 . For the (t + 1) iteration, the algorithm generates a sample from
. For the (t + 1) iteration, the algorithm generates a sample from 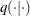 based on the current sample
based on the current sample 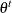 , and it makes a decision to either accept or reject the new sample. If the new sample is accepted, the algorithm repeats
itself by starting at the new sample. If the new sample is rejected, the algorithm starts at the current point and repeats.
The algorithm is self-repeating, so it can be carried out as long as required. In practice, you have to decide the total number
of samples needed in advance and stop the sampler after that many iterations have been completed.
, and it makes a decision to either accept or reject the new sample. If the new sample is accepted, the algorithm repeats
itself by starting at the new sample. If the new sample is rejected, the algorithm starts at the current point and repeats.
The algorithm is self-repeating, so it can be carried out as long as required. In practice, you have to decide the total number
of samples needed in advance and stop the sampler after that many iterations have been completed.
Suppose 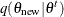 is a symmetric distribution. The proposal distribution should be an easy distribution from which to sample, and it must be
such that
is a symmetric distribution. The proposal distribution should be an easy distribution from which to sample, and it must be
such that 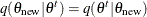 , meaning that the likelihood of jumping to
, meaning that the likelihood of jumping to 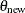 from
from 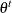 is the same as the likelihood of jumping back to
is the same as the likelihood of jumping back to 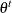 from
from 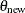 . The most common choice of the proposal distribution is the normal distribution
. The most common choice of the proposal distribution is the normal distribution 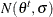 with a fixed
with a fixed  . The Metropolis algorithm can be summarized as follows:
. The Metropolis algorithm can be summarized as follows:
-
Set
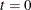 . Choose a starting point
. Choose a starting point 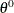 . This can be an arbitrary point as long as
. This can be an arbitrary point as long as 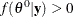 .
.
-
Generate a new sample,
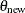 , by using the proposal distribution
, by using the proposal distribution 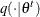 .
.
-
Calculate the following quantity:
![\[ r = \min \left\{ \frac{f(\theta _\mr {new} | {\mb{y}})}{f(\theta ^{t}|{\mb{y}})}, 1 \right\} \]](images/statug_introbayes0075.png)
-
Sample u from the uniform distribution
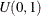 .
.
-
Set
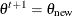 if
if 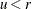 ; otherwise set
; otherwise set 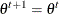 .
.
-
Set
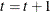 . If
. If 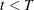 , the number of desired samples, return to step 2. Otherwise, stop.
, the number of desired samples, return to step 2. Otherwise, stop.
Note that the number of iteration keeps increasing regardless of whether a proposed sample is accepted.
This algorithm defines a chain of random variates whose distribution will converge to the desired distribution 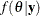 , and so from some point forward, the chain of samples is a sample from the distribution of interest. In Markov chain terminology,
this distribution is called the stationary distribution of the chain, and in Bayesian statistics, it is the posterior distribution of the model parameters. The reason that the Metropolis
algorithm works is beyond the scope of this documentation, but you can find more detailed descriptions and proofs in many
standard textbooks, including Roberts (1996) and Liu (2001). The random-walk Metropolis algorithm is used in the MCMC procedure.
, and so from some point forward, the chain of samples is a sample from the distribution of interest. In Markov chain terminology,
this distribution is called the stationary distribution of the chain, and in Bayesian statistics, it is the posterior distribution of the model parameters. The reason that the Metropolis
algorithm works is beyond the scope of this documentation, but you can find more detailed descriptions and proofs in many
standard textbooks, including Roberts (1996) and Liu (2001). The random-walk Metropolis algorithm is used in the MCMC procedure.
You are not limited to a symmetric random-walk proposal distribution in establishing a valid sampling algorithm. A more general
form, the Metropolis-Hastings (MH) algorithm, was proposed by Hastings (1970). The MH algorithm uses an asymmetric proposal distribution: 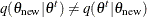 . The difference in its implementation comes in calculating the ratio of densities:
. The difference in its implementation comes in calculating the ratio of densities:
![\[ r = \min \left\{ \frac{f(\theta _\mr {new} | {\mb{y}}) q(\theta ^ t | \theta _\mr {new}) }{f(\theta ^{t}|{\mb{y}}) q(\theta _\mr {new} | \theta ^ t)}, 1 \right\} \]](images/statug_introbayes0083.png)
Other steps remain the same.
The extension of the Metropolis algorithm to a higher-dimensional  is straightforward. Suppose
is straightforward. Suppose 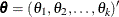 is the parameter vector. To start the Metropolis algorithm, select an initial value for each
is the parameter vector. To start the Metropolis algorithm, select an initial value for each 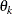 and use a multivariate version of proposal distribution
and use a multivariate version of proposal distribution 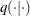 , such as a multivariate normal distribution, to select a k-dimensional new parameter. Other steps remain the same as those previously described, and this Markov chain eventually converges
to the target distribution of
, such as a multivariate normal distribution, to select a k-dimensional new parameter. Other steps remain the same as those previously described, and this Markov chain eventually converges
to the target distribution of 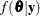 . Chib and Greenberg (1995) provide a useful tutorial on the algorithm.
. Chib and Greenberg (1995) provide a useful tutorial on the algorithm.
Gibbs Sampler
The Gibbs sampler, named by Geman and Geman (1984) after the American physicist Josiah W. Gibbs, is a special case of the Metropolis and Metropolis-Hastings Algorithms in which the proposal distributions exactly match the posterior conditional distributions and proposals are accepted 100% of the time. Gibbs sampling requires you to decompose the joint posterior distribution into full conditional distributions for each parameter in the model and then sample from them. The sampler can be efficient when the parameters are not highly dependent on each other and the full conditional distributions are easy to sample from. Some researchers favor this algorithm because it does not require an instrumental proposal distribution as Metropolis methods do. However, while deriving the conditional distributions can be relatively easy, it is not always possible to find an efficient way to sample from these conditional distributions.
Suppose 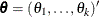 is the parameter vector,
is the parameter vector, 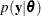 is the likelihood, and
is the likelihood, and 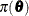 is the prior distribution. The full posterior conditional distribution of
is the prior distribution. The full posterior conditional distribution of 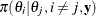 is proportional to the joint posterior density; that is,
is proportional to the joint posterior density; that is,
![\[ \pi (\theta _ i | \theta _ j, i \neq j, \mb{y}) \propto p(\mb{y}|\btheta ) \pi (\btheta ) \]](images/statug_introbayes0092.png)
For instance, the one-dimensional conditional distribution of 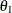 given
given 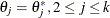 , is computed as the following:
, is computed as the following:
![\[ \pi (\theta _1 | \theta _ j=\theta _ j^*, 2\leq j \leq k, \mb{y}) = p(\mb{y}|(\btheta =(\theta _1, \theta ^*_2,\ldots ,\theta ^*_ k)’) \pi (\btheta =(\theta _1, \theta ^*_2,\ldots ,\theta ^*_ k)’) \]](images/statug_introbayes0095.png)
The Gibbs sampler works as follows:
-
Set
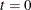 , and choose an arbitrary initial value of
, and choose an arbitrary initial value of 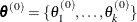 .
.
-
Generate each component of
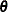 as follows:
as follows:
-
draw
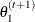 from
from 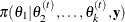
-
draw
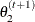 from
from 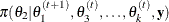
-
…
-
draw
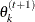 from
from 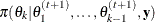
-
-
Set
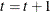 . If
. If 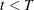 , the number of desired samples, return to step 2. Otherwise, stop.
, the number of desired samples, return to step 2. Otherwise, stop.
The name "Gibbs" was introduced by Geman and Geman (1984). Gelfand et al. (1990) first used Gibbs sampling to solve problems in Bayesian inference. See Casella and George (1992) for a tutorial on the sampler. The GENMOD, LIFEREG, and PHREG procedures update parameters using the Gibbs sampler.
Adaptive Rejection Sampling Algorithm
The GENMOD, LIFEREG, and PHREG procedures use the adaptive rejection sampling (ARS) algorithm to sample parameters sequentially from their univariate full conditional distributions. The ARS algorithm is a rejection algorithm that was originally proposed by Gilks and Wild (1992). Given a log-concave density (the log of the density is concave), you can construct an envelope for the density by using linear segments. You then use the linear segment envelope as a proposal density (it becomes a piecewise exponential density on the original scale and is easy to generate samplers from) in the rejection sampling.
The log-concavity condition is met in some of the models that are fit by the procedures. For example, the posterior densities for the regression parameters in the generalized linear models are log-concave under flat priors. When this condition fails, the ARS algorithm calls for an additional Metropolis-Hastings step (Gilks, Best, and Tan 1995), and the modified algorithm becomes the adaptive rejection Metropolis sampling (ARMS) algorithm. The GENMOD, LIFEREG, and PHREG procedures can recognize whether a model is log-concave and select the appropriate sampler for the problem at hand.
Although samples obtained from the ARMS algorithm often exhibit less dependence with lower autocorrelations, the algorithm could have a high computational cost because it requires repeated evaluations of the objective function (usually five to seven repetitions) at each iteration for each univariate parameter.[2]
Implementation the ARMS algorithm in the GENMOD, LIFEREG, and PHREG procedures is based on code that is provided by Walter R. Gilks, University of Leeds (Gilks 2003). For a detailed description and explanation of the algorithm, see Gilks and Wild (1992); Gilks, Best, and Tan (1995).
Slice Sampler
The slice sampler (Neal 2003), like the ARMS algorithm, is a general algorithm that can be used to sample parameters from their target distribution. As
with the ARMS algorithm, the only requirement of the slice sampler is the ability to evaluate the objective function (the
unnormalized conditional distribution in a Gibbs step, for example) at a given parameter value. In theory, you can draw a
random number from any given distribution as long as you can first obtain a random number uniformly under the curve of that
distribution. Treat the area under the curve of 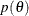 as a two-dimensional space that is defined by the
as a two-dimensional space that is defined by the 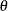 -axis and the Y-axis, the latter being the axis for the density function. You draw uniformly in that area, obtain a two-dimensional
vector of
-axis and the Y-axis, the latter being the axis for the density function. You draw uniformly in that area, obtain a two-dimensional
vector of 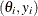 , ignore the
, ignore the 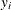 , and keep the
, and keep the 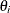 . The
. The 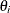 ’s are distributed according to the right density.
’s are distributed according to the right density.
To solve the problem of sampling uniformly under the curve, Neal (2003) proposed the idea of slices (hence the name of the sampler), which can be explained as follows:
-
Start the algorithm at
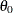 .
.
-
Calculate the objective function
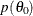 and draw a line between
and draw a line between 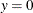 and
and 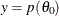 , which defines a vertical slice. You draw a uniform number,
, which defines a vertical slice. You draw a uniform number, 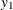 , on this slice, between
, on this slice, between 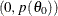 .
.
-
Draw a horizontal line at
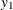 and find the two points where the line intercepts with the curve,
and find the two points where the line intercepts with the curve, 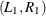 . These two points define a horizontal slice. Draw a uniform number,
. These two points define a horizontal slice. Draw a uniform number, 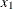 , on this slice, between
, on this slice, between 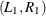 .
.
-
Repeat steps 2 and 3 many times.
The challenging part of the algorithm is finding the horizontal slice 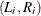 at each iteration. The closed form expressions of
at each iteration. The closed form expressions of 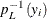 and
and 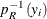 are virtually impossible to obtain analytically in most problems. Neal (2003) proved that although exact solutions would be nice, devising a search algorithm that finds portions of this horizontal slice
is sufficient for the sampler to work. The search algorithm is based on the rejection method to expand and contract, when
needed.
are virtually impossible to obtain analytically in most problems. Neal (2003) proved that although exact solutions would be nice, devising a search algorithm that finds portions of this horizontal slice
is sufficient for the sampler to work. The search algorithm is based on the rejection method to expand and contract, when
needed.
The sampler is implemented as an optional algorithm in the MCMC procedure, where you can use it to draw either model parameters or random-effects parameters. As with the ARMS algorithm, only the univariate version of the slice sampler is implemented. The slice sampler requires repeated evaluations of the objective function; this happens in the search algorithm to identify each horizontal slice at every iteration. Hence, the computational cost could be high if each evaluation of the objective function requires one pass through the entire data set.
Independence Sampler
Another type of Metropolis algorithm is the "independence" sampler. It is called the independence sampler because the proposal distribution in the algorithm does not depend on the current point as it does with the random-walk Metropolis algorithm. For this sampler to work well, you want to have a proposal distribution that mimics the target distribution and have the acceptance rate be as high as possible.
-
Set
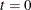 . Choose a starting point
. Choose a starting point 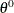 . This can be an arbitrary point as long as
. This can be an arbitrary point as long as 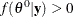 .
.
-
Generate a new sample,
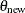 , by using the proposal distribution
, by using the proposal distribution 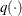 . The proposal distribution does not depend on the current value of
. The proposal distribution does not depend on the current value of 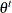 .
.
-
Calculate the following quantity:
![\[ r = \min \left\{ \frac{f(\theta _\mr {new} | {\mb{y}}) / q(\theta _\mr {new})}{f(\theta ^{t}|{\mb{y}}) / q(\theta ^{t})}, 1 \right\} \]](images/statug_introbayes0118.png)
-
Sample u from the uniform distribution
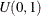 .
.
-
Set
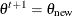 if
if 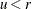 ; otherwise set
; otherwise set 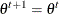 .
.
-
Set
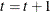 . If
. If 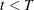 , the number of desired samples, return to step 2. Otherwise, stop.
, the number of desired samples, return to step 2. Otherwise, stop.
A good proposal density should have thicker tails than those of the target distribution. This requirement sometimes can be difficult to satisfy especially in cases where you do not know what the target posterior distributions are like. In addition, this sampler does not produce independent samples as the name seems to imply, and sample chains from independence samplers can get stuck in the tails of the posterior distribution if the proposal distribution is not chosen carefully. The MCMC procedure uses the independence sampler.
Gamerman Algorithm
The Gamerman algorithm, named after the inventor Dani Gamerman, is a special case of the Metropolis algorithm (see the section Metropolis and Metropolis-Hastings Algorithms) in which the proposal distribution is derived from one iteration of the iterative weighted least squares (IWLS) algorithm. As the name suggests, a weighted least squares algorithm is carried out inside an iteration loop. For each iteration, a set of weights for the observations is used in the least squares fit. The weights are constructed by applying a weight function to the current residuals. The proposal distribution uses the current iteration’s values of the parameters to form the proposal distribution from which to generate a proposed random value (Gamerman 1997).
The multivariate sampling algorithm is simple but practical, and can be used to obtain random samples from the posterior distribution of the regression parameters in a generalized linear model (GLM). See Generalized Linear Regression in Chapter 4: Introduction to Regression Procedures, for further details on generalized linear regression models. See McCullagh and Nelder (1989) for a discussion of transformed observations and diagonal matrix of weights pertaining to IWLS.
The GENMOD procedure uses the Gamerman algorithm to sample parameters from their multivariate posterior conditional distributions. For a detailed description and explanation of the algorithm, see Gamerman (1997).
Hamiltonian Monte Carlo Sampler
The Hamiltonian Monte Carlo (HMC) algorithm, also known as the hybrid Monte Carlo algorithm, is a version of the Metropolis algorithm that uses gradients information and auxiliary momentum variables to draw samples from the posterior distribution (Neal 2011). The algorithm uses Hamiltonian dynamics to enable distant proposals in the Metropolis algorithm, making it efficient in many scenarios. The HMC algorithm is applicable only to continuous parameters.
HMC translates the target density function to a potential energy function and adds an auxiliary momentum variable  for each model parameter
for each model parameter 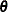 . The resulting joint density has the form
. The resulting joint density has the form
![\[ p(\btheta , \mb{r}) \propto p(\btheta ) \exp \left( -\frac{1}{2}\mb{r}’\mb{r} \right) \]](images/statug_introbayes0120.png)
where 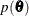 is the posterior of the parameters
is the posterior of the parameters 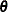 (up to a normalizing constant). HMC draws from the joint space of
(up to a normalizing constant). HMC draws from the joint space of 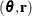 , throws away
, throws away  , and retains
, and retains 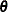 as samples from
as samples from 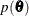 . The algorithm uses the idea of Hamiltonian dynamics in preserving the total energy of a physics system, in which
. The algorithm uses the idea of Hamiltonian dynamics in preserving the total energy of a physics system, in which 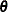 is part of the potential energy function and
is part of the potential energy function and  is part of the kinetic energy (velocity). As the velocity changes, the potential energy changes accordingly, leading to the
movements in the parameter space.
is part of the kinetic energy (velocity). As the velocity changes, the potential energy changes accordingly, leading to the
movements in the parameter space.
At each iteration, HMC first generates the momentum variables  , usually from standard normal distributions, that are independent of
, usually from standard normal distributions, that are independent of 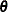 . Then the algorithm follows with a Metropolis update that includes many steps along a trajectory while maintaining the total
energy of the system. One of the most frequently used methods in moving along this trajectory is the leapfrog method, which
involves L steps with a step size
. Then the algorithm follows with a Metropolis update that includes many steps along a trajectory while maintaining the total
energy of the system. One of the most frequently used methods in moving along this trajectory is the leapfrog method, which
involves L steps with a step size  ,
,
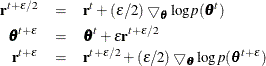
where 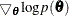 is the gradient of the log-posterior with respect to
is the gradient of the log-posterior with respect to 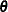 . After L steps, the proposed state
. After L steps, the proposed state 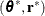 is accepted as the next state of the Markov chain with probability
is accepted as the next state of the Markov chain with probability  .
.
Although HMC can lead to rapid convergence, it also heavily relies on two requirements: the gradient calculation of the logarithm
of the posterior density and carefully selected tuning parameters, in step size  and number of steps L. Step sizes that are too large or too small can lead to overly low or overly high acceptance rates, both of which affect
the convergence of the Markov chain. Large L leads to large trajectory length (
and number of steps L. Step sizes that are too large or too small can lead to overly low or overly high acceptance rates, both of which affect
the convergence of the Markov chain. Large L leads to large trajectory length (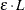 ), which can move the parameters back to their original positions. Small L limits the movement of the chain. To tune
), which can move the parameters back to their original positions. Small L limits the movement of the chain. To tune  and L, you usually want to run a few trials, starting with a small number of L and an
and L, you usually want to run a few trials, starting with a small number of L and an  with a value around 0.1. See Neal (2011) for advice on tuning these parameters.
with a value around 0.1. See Neal (2011) for advice on tuning these parameters.
An example of adaptive HMC with automatic tuning of  and L is the No-U-Turn Sampler (NUTS; Hoffman and Gelman 2014). The NUTS algorithm uses a doubling process to build a binary tree whose leaf nodes correspond to the states of the parameters
and momentum variables. The initial tree has a single node with no heights (
and L is the No-U-Turn Sampler (NUTS; Hoffman and Gelman 2014). The NUTS algorithm uses a doubling process to build a binary tree whose leaf nodes correspond to the states of the parameters
and momentum variables. The initial tree has a single node with no heights (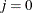 ). The doubling process expands the tree either left or right in a binary fashion, and in each direction, the algorithm takes
). The doubling process expands the tree either left or right in a binary fashion, and in each direction, the algorithm takes
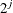 leapfrog steps of size
leapfrog steps of size  . Obviously, as the height of the tree (j) increases, the computational cost increases dramatically. The tree expands until one sampling trajectory makes a U-turn
and starts to revisit parameter space that has been already explored. The NUTS algorithm tunes
. Obviously, as the height of the tree (j) increases, the computational cost increases dramatically. The tree expands until one sampling trajectory makes a U-turn
and starts to revisit parameter space that has been already explored. The NUTS algorithm tunes  so that the actual acceptance rate during the doubling process is close to a predetermined target acceptance probability
so that the actual acceptance rate during the doubling process is close to a predetermined target acceptance probability
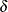 (usually set to 0.6 or higher). When the tuning stage ends, the NUTS algorithm proceeds to the main sampling stage and starts
to draw posterior samples that have a fixed
(usually set to 0.6 or higher). When the tuning stage ends, the NUTS algorithm proceeds to the main sampling stage and starts
to draw posterior samples that have a fixed  value. Increasing the targeted acceptance probability
value. Increasing the targeted acceptance probability 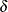 can often improve mixing, but it can also slow down the process significantly. For more information about the NUTS algorithm
and its efficiency, see Hoffman and Gelman (2014).
can often improve mixing, but it can also slow down the process significantly. For more information about the NUTS algorithm
and its efficiency, see Hoffman and Gelman (2014).
Burn-In, Thinning, and Markov Chain Samples
Burn-in refers to the practice of discarding an initial portion of a Markov chain sample so that the effect of initial values on
the posterior inference is minimized. For example, suppose the target distribution is 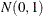 and the Markov chain was started at the value
and the Markov chain was started at the value 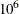 . The chain might quickly travel to regions around 0 in a few iterations. However, including samples around the value
. The chain might quickly travel to regions around 0 in a few iterations. However, including samples around the value 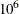 in the posterior mean calculation can produce substantial bias in the mean estimate. In theory, if the Markov chain is run
for an infinite amount of time, the effect of the initial values decreases to zero. In practice, you do not have the luxury
of infinite samples. In practice, you assume that after t iterations, the chain has reached its target distribution and you can throw away the early portion and use the good samples
for posterior inference. The value of t is the burn-in number.
in the posterior mean calculation can produce substantial bias in the mean estimate. In theory, if the Markov chain is run
for an infinite amount of time, the effect of the initial values decreases to zero. In practice, you do not have the luxury
of infinite samples. In practice, you assume that after t iterations, the chain has reached its target distribution and you can throw away the early portion and use the good samples
for posterior inference. The value of t is the burn-in number.
With some models you might experience poor mixing (or slow convergence) of the Markov chain. This can happen, for example,
when parameters are highly correlated with each other. Poor mixing means that the Markov chain slowly traverses the parameter
space (see the section Visual Analysis via Trace Plots for examples of poorly mixed chains) and the chain has high dependence. High sample autocorrelation can result in biased
Monte Carlo standard errors. A common strategy is to thin the Markov chain in order to reduce sample autocorrelations. You thin a chain by keeping every kth simulated draw from each sequence. You can safely use a thinned Markov chain for posterior inference as long as the chain
converges. It is important to note that thinning a Markov chain can be wasteful because you are throwing away a 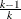 fraction of all the posterior samples generated. MacEachern and Berliner (1994) show that you always get more precise posterior estimates if the entire Markov chain is used. However, other factors, such
as computer storage or plotting time, might prevent you from keeping all samples.
fraction of all the posterior samples generated. MacEachern and Berliner (1994) show that you always get more precise posterior estimates if the entire Markov chain is used. However, other factors, such
as computer storage or plotting time, might prevent you from keeping all samples.
To use the BCHOICE, FMM, GENMOD, LIFEREG, MCMC, and PHREG procedures, you need to determine the total number of samples to keep ahead of time. This number is not obvious and often depends on the type of inference you want to make. Mean estimates do not require nearly as many samples as small-tail percentile estimates. In most applications, you might find that keeping a few thousand iterations is sufficient for reasonably accurate posterior inference. In all four procedures, the relationship between the number of iterations requested, the number of iterations kept, and the amount of thinning is as follows:
![\[ \mr{kept} = \left[ \frac{\mr{requested}}{\mr{thinning}} \right] \]](images/statug_introbayes0136.png)
where ![$\left[ ~ \right]$](images/statug_introbayes0137.png) is the rounding operator.
is the rounding operator.
[2] The extension to the multivariate ARMS algorithm is possible in theory but problematic in practice because the computational cost associated with constructing a multidimensional hyperbola envelop is often prohibitive.