-
ALPHA=

-
specifies that interval estimation of parameters
be done at the 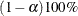 confidence level. The smaller the
confidence level. The smaller the  value, the higher the confidence level. By default,
value, the higher the confidence level. By default, 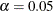 , which corresponds to a 95% confidence interval.
, which corresponds to a 95% confidence interval.
-
ALPHAECV=

-
specifies a  confidence interval
(
confidence interval
( ) for the Browne and Cudeck (1993) expected cross-validation index (ECVI). By default,
) for the Browne and Cudeck (1993) expected cross-validation index (ECVI). By default, 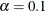 , which corresponds to a 90% confidence interval for the ECVI.
, which corresponds to a 90% confidence interval for the ECVI.
-
ALPHALEV=

ALPHALEVERAGE=
-
specifies the  -level criterion for detecting leverage observations (or leverage points) in case-level (observation-level) residual diagnostics.
The default ALPHALEV= value is 0.01. An observation is a leverage observation if the p-value of its squared Mahalanobis distance (M-distance) for its predictor variables (including observed and latent variables)
is smaller than the specified
-level criterion for detecting leverage observations (or leverage points) in case-level (observation-level) residual diagnostics.
The default ALPHALEV= value is 0.01. An observation is a leverage observation if the p-value of its squared Mahalanobis distance (M-distance) for its predictor variables (including observed and latent variables)
is smaller than the specified  -level, where the p-value is computed according to an appropriate theoretical chi-square distribution. The larger the ALPHALEV= value, the more
liberal the criterion for detecting leverage observations.
-level, where the p-value is computed according to an appropriate theoretical chi-square distribution. The larger the ALPHALEV= value, the more
liberal the criterion for detecting leverage observations.
In addition to displaying the leverage observations as defined by the ALPHALEV= criterion, PROC CALIS also displays the next
5 observations with the largest leverage M-distances for reference. However, the total number of observations in the displayed
output cannot exceed 30 or the number of original observations, whichever is smaller.
This option is relevant only when residual analysis is requested with the RESIDUAL
option and with raw data input.
-
ALPHAOUT=

ALPHAOUTLIER=
-
specifies the  -level criterion for detecting outliers in case-level (observation-level) residual diagnostics. The default ALPHAOUT= value
is 0.01. An observation is an outlier if the p-value of its squared residual M-distance is smaller than the specified
-level criterion for detecting outliers in case-level (observation-level) residual diagnostics. The default ALPHAOUT= value
is 0.01. An observation is an outlier if the p-value of its squared residual M-distance is smaller than the specified  -level, where the p-value is computed according to an appropriate theoretical chi-square distribution. The larger the ALPHAOUT= value, the more
liberal the criterion for detecting outliers.
-level, where the p-value is computed according to an appropriate theoretical chi-square distribution. The larger the ALPHAOUT= value, the more
liberal the criterion for detecting outliers.
In addition to displaying the outliers as defined by the ALPHAOUT= criterion, PROC CALIS also displays the next 5 observations
with the largest residual M-distances for reference. However, the total number of observations in the displayed output in
the displayed output cannot exceed 30 or the number of original observations, whichever is smaller.
This option is relevant only when residual analysis is requested with the RESIDUAL
option and with raw data input.
-
ALPHARMS=

ALPHARMSEA=
-
specifies a 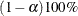 confidence
interval (
confidence
interval (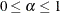 ) for the Steiger and Lind (1980) root mean square error of approximation (RMSEA) coefficient (see Browne and Du Toit 1992). The default value is
) for the Steiger and Lind (1980) root mean square error of approximation (RMSEA) coefficient (see Browne and Du Toit 1992). The default value is 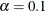 , which corresponds to a 90% confidence interval for the RMSEA.
, which corresponds to a 90% confidence interval for the RMSEA.
-
ASINGULAR=r
ASING=r
-
specifies an absolute singularity criterion r (r > 0),
for the inversion of the information matrix, which is needed to compute the covariance matrix. The default value for r or ASING= is the square root of the smallest positive double precision value.
When inverting the information matrix, the following singularity criterion is used for the diagonal pivot 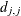 of the matrix:
of the matrix:
where VSING and MSING are the specified values in the VSINGULAR=
and MSINGULAR=
options, respectively, and 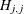 is the jth diagonal element of the information matrix. Note that in many cases a normalized matrix
is the jth diagonal element of the information matrix. Note that in many cases a normalized matrix 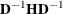 is decomposed (where
is decomposed (where 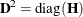 ), and the singularity criteria are modified correspondingly.
), and the singularity criteria are modified correspondingly.
-
ASYCOV=name
ASC=name
-
specifies the formula for asymptotic covariances used in the weight matrix 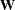 for WLS and DWLS estimation. The ASYCOV option is effective only if METHOD=
WLS or METHOD=
DWLS and no INWGT=
input data set is specified. The following formulas are implemented:
for WLS and DWLS estimation. The ASYCOV option is effective only if METHOD=
WLS or METHOD=
DWLS and no INWGT=
input data set is specified. The following formulas are implemented:
- BIASED:
-
Browne (1984) formula (3.4) biased asymptotic covariance estimates; the resulting weight matrix is at least positive semidefinite. This
is the default for analyzing a covariance matrix.
- UNBIASED:
-
Browne (1984) formula (3.8) asymptotic covariance estimates corrected for bias; the resulting weight matrix can be indefinite (that is,
can have negative eigenvalues), especially for small N.
- CORR:
-
Browne and Shapiro (1986) formula (3.2) (identical to De Leeuw (1983) formulas (2,3,4)) the asymptotic variances of the diagonal elements are set to the reciprocal of the value r specified by the WPENALTY=
option (default: r=100). This formula is the default for analyzing a correlation matrix.
By default, AYSCOV=BIASED is used for covariance analyses and ASYCOV=CORR is used for correlation analyses. Therefore, in
almost all cases you do not need to set the ASYCOV= option once you specify the covariance or correlation analysis by the
COV
or CORR
option.
-
BASEFIT=SAS-data-set
INBASEFIT=SAS-data-set
-
inputs the SAS-data-set that contains
the fit information of the baseline model of your choice. This customized baseline model replaces the default uncorrelatedness
model for computing several fit indices of your target model. Typically, you create the BASEFIT= data set by using the OUTFIT=
option in a previous PROC CALIS fitting of your customized baseline model. Using the BASEFIT= option assumes that you fit
your customized baseline model and your target model with the same data, number of groups (for multiple-group analysis), and
estimation method. Typically, your baseline model should be more restrictive (or have fewer parameters) than your target model.
For example, the following statements use the compound symmetry model (COVPATTERN=
COMPSYM) as the customized baseline model for the subsequent factor model with two factors:
proc calis data=abc outfit=outf method=gls covpattern=compsym;
var=x1-x10;
run;
proc calis data=abc method=gls basefit=outf;
factor n=2;
var=x1-x10;
run;
The fit information of the customized baseline model is saved as an OUTFIT= data set called outf, which is then read as a BASEFIT= data set in the next PROC CALIS run for fitting the target factor model. Notice that in
this example the baseline model and the target factor model use the same data set, abc, and the same GLS estimation method.
Alternatively, you can use the BASEFUNC=
option to input the function value and the degrees of freedom of your customized baseline model. See the BASEFUNC=
option for details. The BASEFIT= option is ignored if you also specify the BASEFUNC= option.
Notice that the fit information in the BASEFIT= data set does not affect the computation of all fit indices. Mainly, it affects
the incremental fit indices, because these indices are defined as the incremental fit of a target model over a baseline model.
Among all absolute and parsimonious fit indices, only the parsimonious goodness-of-fit (PGFI) index (Mulaik et al. 1989) is affected by the input fit information provided in the BASEFIT= data set.
If you specify METHOD=
LSDWLS, LSFIML, LSGLS, LSML, or LSMLSB for your target model, the fit information in the BASEFIT= data set is assumed to have
been obtained from the DWLS, FIML, GLS, ML, or MLSB estimation of your customized baseline model. Hence, the fit information
in the BASEFIT= data set applies only to the second estimation of your target model. The unweighted least squares (ULS) estimation
of the target model still uses the uncorrelatedness model as the baseline model for computing fit indices.
If you specify METHOD=
MLSB or LSMLSB for your target model, the fit information in the BASEFIT= data set is assumed to have been obtained from an
ML estimation with the Satorra-Bentler scale correction on the model fit chi-square (METHOD=MLSB). The BASEFIT= data set should
contain the information about the unadjusted chi-square and the SB-scaled chi-square so that the computation of the fit indices
can take the scale correction into account.
If you use a BASEFIT= data set to input the fit information of your customized baseline model in a multiple-group analysis,
then the baseline model function values, chi-squares, and degrees of freedom for individual groups are not known and hence
not displayed in the multiple-group fit summary table. The Bentler-Bonett normed fit index (NFI) is also not displayed in
the multiple-group fit summary table, because the baseline model function values for individual groups are not saved in the
BASEFIT= data set.
-
BASEFUNC=r(<DF=>i)
BASEFUNC(<DF=>i)=r
-
inputs the fit function value r and the degrees of freedom i of the baseline model of your choice.
This customized baseline model replaces the default uncorrelatedness model for computing several fit indices of your target
model. To use this option, you must first fit your customized baseline model and then use this option to input the baseline
model fit information when you fit your target model.
Using the BASEFUNC= option assumes that you fit your customized baseline model and your target model with the same data, number
of groups (for multiple-group analysis), and estimation method. Typically, your baseline model should be more restrictive
(or have fewer parameters) than your target model.
For example, assume that after fitting a customized baseline model you find that the function value of the baseline model
is 20.54 and the model degrees of freedom are 15. The following code inputs the function value and the degrees of freedom
of the customized baseline model by using the BASEFUNC= option:
proc calis data=abc basefunc(df=15)=20.54;
path
f1 ===> x1-x5 = 1.,
f2 ===> x6-x10 = 1.,
f1 ===> f2;
run;
You can use the following equivalent syntax to provide the same baseline model fit information:
basefunc(df=15)=20.54
basefunc(15)=20.54
basefunc=20.54(df=15)
basefunc=20.54(15)
It is emphasized here that you should input the fit function value, but not the model fit chi-square value, of the baseline
model in the BASEFUNC= option. For all estimation methods except the full information maximum likelihood (FIML) method in
PROC CALIS, the model fit chi-square values are some multiples of the fit function values. See the section Estimation Criteria for the definitions of the various fit functions that are assumed by the BASEFUNC= option.
Alternatively, it might be easier to use the BASEFIT=
option to specify the SAS data set that contains the baseline model fit information. Such a SAS data set is typically created
by using the OUTFIT=
option in the PROC CALIS fitting of your customized baseline model. See the BASEFIT=
option for details. However, the BASEFIT= option is ignored if you also specify the BASEFUNC= option.
Notice that the specified values in the BASEFUNC= option do not affect the computation of all fit indices. Mainly, they affect
the incremental fit indices, because these indices are defined as the incremental fit of a target model over a baseline model.
Among all absolute and parsimonious fit indices, only the parsimonious goodness-of-fit (PGFI) index (Mulaik et al. 1989) is affected by the values provided in the BASEFUNC= option.
If you specify METHOD=
LSDWLS, LSFIML, LSGLS, LSML, or LSMLSB for your target model, the fit information that the BASEFUNC= option provides is assumed
to have been obtained from the DWLS, FIML, GLS, ML, or MLSB estimation of your customized baseline model. Hence, the fit information
that the BASEFUNC= option provides applies only to the second estimation of your target model. The unweighted least squares
(ULS) estimation of the target model still uses the uncorrelatedness model as the baseline model for computing fit indices.
If you specify METHOD=
MLSB or LSMLSB for your target model, you must be careful to input an appropriate BASEFUNC= value. Because the BASEFUNC= value
is used directly to compute fit indices, the Satorra-Bentler scaling constant for the baseline model is unavailable to PROC
CALIS for computing various fit indices. An appropriate step is to rescale the original baseline model fit function value
before inputting it as the BASEFUNC= value. For example, suppose that you fitted a baseline model by using METHOD=MLSB. The
function value was f, the unadjusted chi-square was u, and the Satorra-Bentler scaled chi-square was s. Instead of using f, you should use the value of f s
s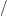 u as the input BASEFUNC= value. This way the fit indices that are computed for the target model would be based on the scaled
chi-squares of the baseline and target models.
u as the input BASEFUNC= value. This way the fit indices that are computed for the target model would be based on the scaled
chi-squares of the baseline and target models.
If you use the BASEFUNC= option to input the fit information of your customized baseline model in a multiple-group analysis,
then the baseline model function values, chi-squares, and degrees of freedom for individual groups are not known and hence
not displayed in the multiple-group fit summary table. The Bentler-Bonett NFI is also not displayed in the multiple-group
fit summary table, because the baseline model function values for individual groups are not provided with the BASEFUNC= option.
-
BIASKUR
-
computes univariate skewness and
kurtosis by formulas uncorrected for bias.
See the section Measures of Multivariate Kurtosis for more information.
-
CHICORRECT= name | c
CHICORR= name | c
-
specifies a correction factor c for the chi-square statistics for model fit.
You can specify a name for a built-in correction factor or a value between 0 and 1 as the CHICORRECT= value. The model fit chi-square statistic
is computed as:
where N is the total number of observations, k is the number of independent groups, and F is the optimized function value. Application of these correction factors requires appropriate specification of the covariance
structural model suitable for the chi-square correction. For example, using CHICORRECT=UNCORR assumes that you are fitting
a covariance structure with free parameters on the diagonal elements and fixed zeros off-diagonal elements of the covariance
matrix. Because all the built-in correction factors assume multivariate normality in their derivations, the appropriateness
of applying these built-in chi-square corrections to estimation methods other than METHOD=
is not known. The CHICORRECT= option is ignored when you specify METHOD=
MLSB, which has its own correction factor on the model fit chi-square statistics.
Valid names for the CHICORRECT= value are as follows:
- COMPSYM | EQVARCOV
-
specifies the correction factor due to Box (1949) for testing equal variances and equal covariances in a covariance matrix. The correction factor is:
where p (p > 1) represents the number of variables and 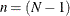 , with N denoting the number of observations in a single group analysis. This option is not applied when you also analyze the mean
structures or when you fit multiple-group models.
, with N denoting the number of observations in a single group analysis. This option is not applied when you also analyze the mean
structures or when you fit multiple-group models.
- EQCOVMAT
-
specifies the correction factor due to Box (1949) for testing equality of covariance matrices. The correction factor is:
where p represents the number of variables, k (k > 1) represents the number of groups, and 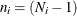 , with
, with 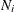 denoting the number of observations in the ith group. This option is not applied when you also analyze the mean structures or when you fit single-group models.
denoting the number of observations in the ith group. This option is not applied when you also analyze the mean structures or when you fit single-group models.
- FIXCOV
-
specifies the correction factor due to Bartlett (1954) for testing a covariance matrix against a hypothetical fixed covariance matrix. The correction factor is:
where p represents the number of variables and 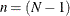 , with N denoting the number of observations in a single group analysis. This option is not applied when you also analyze the mean
structures or when you fit multiple-group models.
, with N denoting the number of observations in a single group analysis. This option is not applied when you also analyze the mean
structures or when you fit multiple-group models.
- SPHERICITY
-
specifies the correction factor due to Box (1949) for testing a spherical covariance matrix (Mauchly 1940). The correction factor is:
where p represents the number of variables and 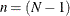 , with N denoting the number of observations in a single group analysis. This option is not applied when you also analyze the mean
structures or when you fit multiple-group models.
, with N denoting the number of observations in a single group analysis. This option is not applied when you also analyze the mean
structures or when you fit multiple-group models.
- TYPEH
-
specifies the correction factor for testing the H pattern (Huynh and Feldt 1970) directly. The correction factor is:
where p (p > 1) represents the number of variables and 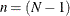 , with N denoting the number of observations in a single group analysis. This option is not applied when you also analyze the mean
structures or when you fit multiple-group models.
, with N denoting the number of observations in a single group analysis. This option is not applied when you also analyze the mean
structures or when you fit multiple-group models.
This correction factor is derived by substituting p with p – 1 in the correction formula applied to Mauchly’s sphericity test. The reason is that testing the H pattern of p variables is equivalent to testing the sphericity of the (p – 1) orthogonal contrasts of the same set of variables (Huynh and Feldt 1970). See pp. 295–296 of Morrison (1990) for more details.
- UNCORR
-
specifies the correction factor due to Bartlett (1950) and Box (1949) for testing a diagonal pattern of a covariance matrix, while the diagonal elements (variances) are unconstrained. This test
is sometimes called Bartlett’s test of sphericity—not to be confused with the sphericity test dues to Mauchly (1940), which requires all variances in the covariance matrix to be equal. The correction factor is:
where p represents the number of variables and 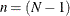 , with N denoting the number of observations in a single group analysis. This option is not applied when you also analyze the mean
structures or when you fit multiple-group models.
, with N denoting the number of observations in a single group analysis. This option is not applied when you also analyze the mean
structures or when you fit multiple-group models.
-
CI
CL
-
prints the confidence intervals or limits for parameters.
By default, PROC CALIS estimates the lower and upper confidence limits at the 95% confidence level, which corresponds to the
default value of the ALPHA= option (0.05). You can change the default level of confidence by specifying the ALPHA=
option.
-
CLOSEFIT=p
-
defines the criterion value p for indicating a close fit. The smaller the better fit.
The default value for close fit is .05.
-
CORRELATION
CORR
-
analyzes the correlation matrix, instead of the default covariance matrix.
See the COVARIANCE
option for more details.
-
COVARIANCE
COV
-
analyzes the covariance matrix. Because this is also the default analysis
in PROC CALIS, you can simply omit this option when you analyze covariance rather than correlation matrices. If the DATA=
input data set is a TYPE=CORR data set (containing a correlation matrix and standard deviations), the default COV option
means that the covariance matrix is computed and analyzed.
Unlike many other SAS/STAT procedures (for example, the FACTOR procedure) that analyze correlation matrices by default, PROC
CALIS uses a different default because statistical theories of structural equation modeling or covariance structure analysis
are mostly developed for covariance matrices. You must use the CORR
option if correlation matrices are analyzed.
-
COVPATTERN=name
COVPAT=name
-
specifies one of the built-in covariance structures for the
data. The purpose of this option is to fit some commonly-used direct covariance structures efficiently without the explicit
use of the MSTRUCT model specifications. With this option, the covariance structures are defined internally in PROC CALIS.
The following names for the built-in covariance structures are supported:
- COMPSYM | EQVARCOV
-
specifies the compound symmetry pattern for the covariance matrix. That is, a covariance matrix with equal variances for all
variables and equal covariance between any pairs of variables (EQVARCOV). For example, if there are four variables in the
analysis, the covariance pattern generated by PROC CALIS has the following form:
PROC CALIS denotes the common variance parameter, v, by _varparm, and the common covariance parameter, v, by _covparm.
If you request a single-group maximum likelihood (METHOD=ML) covariance structure analysis by specifying the COVPATTERN=COMPSYM
or COVPATTERN=EQVARCOV option and the mean structures are not modeled, the chi-square correction due to Box (1949) is applied automatically when the number of variables is greater than or equal to 2. See the CHICORRECT=
COMPSYM option for the definition of the correction factor.
- EQCOVMAT
-
specifies the equality of covariance matrices between multiple groups. That is, this option tests the null hypothesis that
where 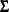 is a common covariance matrix for the k
is a common covariance matrix for the k 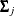 ’s (
’s (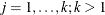 ). The elements of
). The elements of 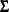 are named
are named _cov_xx_yy automatically by PROC CALIS, where xx and yy represents the row and column numbers such that xx is at least as large as yy. For example, if there are four variables in the analysis, the (1,1) element of 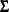 is denoted by
is denoted by _cov_1_1, the (4,3) or (3,4) element of 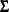 is denoted by
is denoted by _cov_4_3, and so on.
If you request a multiple-group maximum likelihood (METHOD=ML) covariance structure analysis by specifying the COVPATTERN=EQCOVMAT
and the mean structures are not modeled, the chi-square correction due to Box (1949) is applied automatically. See the CHICORRECT=
EQCOVMAT option for the definition of the correction factor.
- SATURATED
-
specifies a saturated covariance structure model. This is the default option when you specify the MEANPATTERN=
option without using the COVPATTERN= option. The elements of 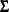 are named
are named _cov_xx_yy automatically by PROC CALIS, where xx represents the row number and yy represents the column number. For example, if there are three variables in the analysis, the (1,1) element in 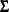 is denoted by
is denoted by _cov_1_1, the (3,2) or (2,3) element in 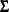 is denoted by
is denoted by _cov_3_2, and so on.
- SPHERICITY | SIGSQI
-
specifies the spheric pattern of the covariance matrix (Mauchly 1940). That is, this option tests the null hypothesis that
where 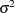 is a common variance parameter and
is a common variance parameter and 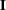 is an identity matrix. For example, if there are three variables in the analysis, the covariance pattern generated by PROC
CALIS is:
is an identity matrix. For example, if there are three variables in the analysis, the covariance pattern generated by PROC
CALIS is:
PROC CALIS denotes the common variance parameter, v, by _varparm.
If you request a single-group maximum likelihood (METHOD=ML) covariance structure analysis by specifying the COVPATTERN=SPHERICITY
or COVPATTERN=SIGSQI option and the mean structures are not modeled, the chi-square correction due to Box (1949) is applied automatically. See the CHICORRECT=
SPHERICITY option for the definition of the correction factor.
- UNCORR | DIAG
-
specifies the diagonal pattern of the covariance matrix. That is, this option tests the null hypothesis of uncorrelatedness—all
correlations (or covariances) between variables are zero and the variances are unconstrained. For example, if there are three
variables in the analysis, the covariance pattern generated by PROC CALIS is:
PROC CALIS denotes the variance parameters 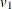 ,
, 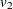 , and
, and 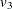 by
by _varparm_1, _varparm_2, and _varparm_3, respectively.
If you request a single-group maximum likelihood (METHOD=ML) covariance structure analysis by specifying the COVPATTERN=UNCORR
or COVPATTERN=DIAG option and the mean structures are not modeled, the chi-square correction due to Bartlett (1950) is applied automatically. See the CHICORRECT=
UNCORR option for the definition of the correction factor. Under the multivariate normal assumption, COVPATTERN=UNCORR is
also a test of independence of the variables in the analysis.
When you specify the covariance structure model by means of the COVPATTERN= option, you can define the set of variables in
the analysis by the VAR
statement (either within the scope of the PROC CALIS statement or the GROUP
statements). If the VAR statement is not used, PROC CALIS uses all numerical variables in the data sets.
Except for the EQCOVMAT pattern, all other built-in covariance patterns are primarily designed for single-group analysis.
However, you can still use these covariance pattern options for multiple-group situations. For example, consider the following
three-group analysis:
proc calis covpattern=compsym;
group 1 / data=set1;
group 2 / data=set2;
group 3 / data=set3;
run;
In this specification, all three groups are fitted by the compound symmetry pattern. However, there would be no constraints
across these groups. PROC CALIS generates two distinct parameters for each group: _varparm_mdl1 and _covparm_mdl1 for Group 1, _varparm_mdl2 and _covparm_mdl2 for Group 2, and _varparm_mdl3 and _covparm_mdl3 for Group 3. Similarly, the _mdlxx suffix, where xx represents the model number, is applied to the parameters defined by the SATURATED, SPHERICITY (or SIGSQI), and UNCORR (or
DIAG) covariance patterns in multiple-group situations. However, chi-square correction, whenever it is applicable to single-group
analysis, is not applied to such multiple-group analyses.
You can also apply the COVPATTERN= option partially to the groups in the analysis. For example, the following statements apply
the spheric pattern to Group 1 and Group 2 only:
proc calis covpattern=sphericity;
group 1 / data=set1;
group 2 / data=set2;
group 3 / data=set3;
model 3 / group=3;
path x1 ===> y3;
run;
Group 3 is fitted by Model 3, which is specified explicitly by a PATH model with distinct covariance structures.
If the EQCOVMAT pattern is specified instead, as shown in the following statements, the equality of covariance matrices still
holds for Groups 1 and 2:
proc calis covpattern=eqcovmat;
group 1 / data=set1;
group 2 / data=set2;
group 3 / data=set3;
model 3 / group=3;
path x1 ===> y3;
run;
However, Group 3 has it own covariances structures as specified in Model 3. In this case, the chi-square correction due to
Box (1949) is not applied because the null hypothesis is no longer testing the equality of covariance matrices among the groups in
the analysis.
Use the MEANPATTERN=
option if you also want to analyze some built-in mean structures along with the covariance structures.
-
COVSING=r
-
specifies a nonnegative threshold r,
which determines whether the eigenvalues of the information matrix are considered to be zero. If the inverse of the information
matrix is found to be singular (depending on the VSINGULAR=
, MSINGULAR=
, ASINGULAR=
, or SINGULAR=
option), a generalized inverse is computed using the eigenvalue decomposition of the singular matrix. Those eigenvalues smaller
than r are considered to be zero. If a generalized inverse is computed and you do not specify the NOPRINT
option, the distribution of eigenvalues is displayed.
-
DATA=SAS-data-set
-
specifies an input data set that can be an
ordinary SAS data set or a specially structured TYPE=CORR, TYPE=COV, TYPE=UCORR, TYPE=UCOV, TYPE=SSCP, or TYPE=FACTOR SAS
data set, as described in the section Input Data Sets. If the DATA= option is omitted, the most recently created SAS data set is used.
-
DEMPHAS=r
DE=r
-
changes the initial values
of all variance parameters by the relationship:
where  is the new initial value and
is the new initial value and 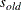 is the original initial value. The value of r must be positive. If you specify an r value less than 1E–8, it is replaced with 1E–8.
is the original initial value. The value of r must be positive. If you specify an r value less than 1E–8, it is replaced with 1E–8.
The initial values of all variance parameters should always be nonnegative to generate positive definite predicted model matrices
in the first iteration. By using values of  , for example, r = 2, r = 10, and so on, you can increase these initial values to produce predicted model matrices with high positive eigenvalues
in the first iteration. The DEMPHAS= option is effective independent of the way the initial values are set; that is, it changes
the initial values set in the model specification as well as those set by an INMODEL=
data set and those automatically generated for the FACTOR, LINEQS, LISMOD, PATH, or RAM models. It also affects the initial
values set by the START=
option, which uses, by default, DEMPHAS=100 if a covariance matrix is analyzed and DEMPHAS=10 for a correlation matrix.
, for example, r = 2, r = 10, and so on, you can increase these initial values to produce predicted model matrices with high positive eigenvalues
in the first iteration. The DEMPHAS= option is effective independent of the way the initial values are set; that is, it changes
the initial values set in the model specification as well as those set by an INMODEL=
data set and those automatically generated for the FACTOR, LINEQS, LISMOD, PATH, or RAM models. It also affects the initial
values set by the START=
option, which uses, by default, DEMPHAS=100 if a covariance matrix is analyzed and DEMPHAS=10 for a correlation matrix.
-
DFREDUCE=i
DFRED=i
-
reduces the degrees of freedom
of the model fit  test by i. In general, the number of degrees of freedom is the total number of nonredundant elements in all moment matrices minus the
number of parameters, t. Because negative values of i are allowed, you can also increase the number of degrees of freedom by using this option.
test by i. In general, the number of degrees of freedom is the total number of nonredundant elements in all moment matrices minus the
number of parameters, t. Because negative values of i are allowed, you can also increase the number of degrees of freedom by using this option.
-
EDF=n
DFE=n
-
makes the effective number of
observations n + 1. You can also use the NOBS=
option to specify the number of observations.
-
EFFPART
TOTEFF
TE
-
computes and displays total, direct, and indirect effects for the unstandardized
and standardized estimation results. Standard errors for the effects are also computed. Note that this displayed output is
not automatically included in the output generated by the PALL
option.
Note also that in some situations computations of total effects and their partitioning are not appropriate. While total and
indirect effects must converge in recursive models (models with no cyclic paths among variables), they do not always converge
in nonrecursive models. When total or indirect effects do not converge, it is not appropriate to partition the effects. Therefore,
before partitioning the total effects, the convergence criterion must be met. To check the convergence of the effects, PROC
CALIS computes and displays the "stability coefficient of reciprocal causation"—
that is, the largest modulus of the eigenvalues of the 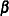 matrix, which is the square matrix that contains the path coefficients of all endogenous variables in the model. Stability
coefficients less than one provide a necessary and sufficient condition for the convergence of the total and the indirect
effects. Otherwise, PROC CALIS does not show results for total effects and their partitioning. See the section Stability Coefficient of Reciprocal Causation for more information about the computation of the stability coefficient.
matrix, which is the square matrix that contains the path coefficients of all endogenous variables in the model. Stability
coefficients less than one provide a necessary and sufficient condition for the convergence of the total and the indirect
effects. Otherwise, PROC CALIS does not show results for total effects and their partitioning. See the section Stability Coefficient of Reciprocal Causation for more information about the computation of the stability coefficient.
-
EXTENDPATH
GENPATH
-
displays the extended path estimates such as the variances,
covariances, means, and intercepts in the table that contains the ordinary path effect (coefficient) estimates. This option
applies to the PATH model only.
-
FCONV=r
FTOL=r
-
specifies the relative function convergence criterion. The optimization
process is terminated when the relative difference of the function values of two consecutive iterations is smaller than the
specified value of r; that is,
where FSIZE can be defined by the FSIZE= option in the NLOPTIONS
statement. The default value is 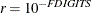 , where FDIGITS either can be specified in the NLOPTIONS
statement or is set by default to
, where FDIGITS either can be specified in the NLOPTIONS
statement or is set by default to 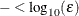 , where
, where  is the machine precision.
is the machine precision.
-
G4=i
-
instructs that the algorithm to compute the approximate
covariance matrix of parameter estimates used for computing the
approximate standard errors and modification
indices when the information matrix is singular. If the number of parameters t used in the model you analyze is smaller than the value of i, the time-expensive Moore-Penrose (G4) inverse of the singular information matrix is computed by eigenvalue decomposition.
Otherwise, an inexpensive pseudo (G1) inverse is computed by sweeping. By default, i = 60.
See the section Estimation Criteria for more details.
-
GCONV=r
GTOL=r
-
specifies the relative gradient convergence criterion.
Termination of all techniques (except the CONGRA technique) requires the following normalized predicted function reduction
to be smaller than r. That is,
where FSIZE can be defined by the FSIZE= option in the NLOPTIONS
statement. For the CONGRA technique (where a reliable Hessian estimate 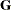 is not available),
is not available),
is used. The default value is 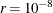 .
.
-
INEST=SAS-data-set
INVAR=SAS-data-set
ESTDATA=SAS-data-set
-
specifies an input data set that
contains initial estimates for the parameters used in the optimization process and can also contain boundary and general linear
constraints on the parameters. Typical applications of this option are to specify an OUTEST=
data set from a previous PROC CALIS analysis. The initial estimates are taken from the values of the PARMS observation in
the INEST= data set.
-
INFORMATION=name
INFORM=name
-
specifies the type of information matrix from which the standard errors are computed. You can specify the following names:
- EXPECTED | EXP
-
requests that the expected information be used.
- OBSERVED | OBS
-
requests that the observed information be used.
By default, METHOD=FIML uses INFORMATION=OBSERVED, whereas METHOD=ML, MLSB, or GLS uses INFORMATION=EXPECTED. You overwrite
the default by using this option. However, for METHOD=WLS, you can specify only INFORMATION=EXPECTED.
-
INMODEL=SAS-data-set
INRAM=SAS-data-set
-
specifies an input data set that contains information about the
analysis model. A typical use of the INMODEL= option is when you run an analysis with its model specifications saved as an
OUTMODEL=
data set from a previous PROC CALIS run. Instead of specifying the main
or subsidiary
model specification statements in the new run, you use the INMODEL= option to input the model specification saved from the
previous run.
Sometimes, you might create an INMODEL= data set from modifying an existing OUTMODEL= data set. However, editing and modifying
OUTMODEL= data sets requires good understanding of the formats and contents of the OUTMODEL= data sets. This process could
be error-prone for novice users. For details about the format of INMODEL= or OUTMODEL= data sets, see the sectionInput Data Sets.
It is important to realize that INMODEL= or OUTMODEL= data sets contain only the information about the specification of the
model. These data sets do not store any information about the bounds on parameters, linear and nonlinear parametric constraints,
and programming statements for computing dependent parameters. If required, these types of information must be provided in
the corresponding statement specifications (for example, BOUNDS
, LINCON
, and so on) in addition to the INMODEL = data set.
An OUTMODEL= data set might also contain default parameters added automatically by PROC CALIS from a previous run (for example,
observations with _TYPE_=ADDPCOV, ADDMEAN, or ADDPVAR). When reading the OUTMODEL= model specification as an INMODEL= data
set in a new run, PROC CALIS ignores these added parameters so that the model being read is exactly like the previous PROC
CALIS specification (that is, before default parameters were added automatically). After interpreting the specification in
the INMODEL= data set, PROC CALIS will then add default parameters appropriate to the new run. The purpose of doing this is
to avoid inadvertent parameter constraints in the new run, where another set of automatic default parameters might have the
same generated names as those of the generated parameter names in the INMODEL= data set.
If you want the default parameters in the INMODEL= data set to be read as a part of model specification, you must also specify
the READADDPARM
option. However, using the READADDPARM
option should be rare.
-
INSTEP=r
-
For highly nonlinear objective functions, such as the EXP function,
the default initial radius of the trust-region algorithms (TRUREG, DBLDOG, and LEVMAR) or the default step length of the line-search
algorithms can produce arithmetic overflows. If an arithmetic overflow occurs, specify decreasing values of 0 < r < 1 such as INSTEP=1E–1, INSTEP=1E–2, INSTEP=1E–4, and so on, until the iteration starts successfully.
-
For trust-region algorithms (TRUREG, DBLDOG, and LEVMAR),
the INSTEP option specifies a positive factor for the initial radius of the trust region. The default initial trust-region
radius is the length of the scaled gradient, and it corresponds to the default radius factor of r = 1.
-
For line-search algorithms (NEWRAP, CONGRA, and QUANEW),
INSTEP specifies an upper bound for the initial step length for the line search during the first five iterations. The default
initial step length is r = 1.
For more details, see the section Computational Problems.
-
INWGT<(INV)>=SAS-data-set
INWEIGHT<(INV)>=SAS-data-set
-
specifies an input data set that
contains the weight matrix 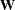 used in generalized least squares (GLS), weighted least squares (WLS, ADF), or diagonally weighted least squares (DWLS) estimation,
if you do not specify the INV option at the same time. The weight matrix must be positive definite because its inverse must
be defined in the computation of the objective function. If the weight matrix
used in generalized least squares (GLS), weighted least squares (WLS, ADF), or diagonally weighted least squares (DWLS) estimation,
if you do not specify the INV option at the same time. The weight matrix must be positive definite because its inverse must
be defined in the computation of the objective function. If the weight matrix 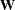 defined by an INWGT= data set is not positive definite, it can be ridged using the WRIDGE=
option. See the section Estimation Criteria for more information. If you specify the INWGT(INV)= option, the INWGT= data set contains the inverse of the weight matrix,
rather than the weight matrix itself. Specifying the INWGT(INV)= option is equivalent to specifying the INWGT= and INWGTINV
options simultaneously. With the INWGT(INV)= specification, the input matrix is not required to be positive definite. See
the INWGTINV
option for more details. If no INWGT= data set is specified, default settings for the weight matrices are used in the estimation
process. The INWGT= data set is described in the section Input Data Sets. Typically, this input data set is an OUTWGT=
data set from a previous PROC CALIS analysis.
defined by an INWGT= data set is not positive definite, it can be ridged using the WRIDGE=
option. See the section Estimation Criteria for more information. If you specify the INWGT(INV)= option, the INWGT= data set contains the inverse of the weight matrix,
rather than the weight matrix itself. Specifying the INWGT(INV)= option is equivalent to specifying the INWGT= and INWGTINV
options simultaneously. With the INWGT(INV)= specification, the input matrix is not required to be positive definite. See
the INWGTINV
option for more details. If no INWGT= data set is specified, default settings for the weight matrices are used in the estimation
process. The INWGT= data set is described in the section Input Data Sets. Typically, this input data set is an OUTWGT=
data set from a previous PROC CALIS analysis.
-
INWGTINV
-
specifies that the INWGT= data set contains the inverse of the weight matrix,
rather than the weight matrix itself. This option is effective only with an input weight matrix specified in the INWGT=
data set and with the generalized least squares (GLS), weighted least squares (WLS or ADF), or diagonally weighted least
squares (DWLS) estimation. With this option, the input matrix provided in the INWGT= data set is not required to be positive
definite. Also, the ridging requested by the WRIDGE=
option is ignored when you specify the INWGTINV option.
-
KURTOSIS
KU
-
computes and displays
univariate kurtosis and skewness, various coefficients of multivariate
kurtosis, and the numbers of observations that contribute most to the normalized multivariate kurtosis. See the section Measures of Multivariate Kurtosis for more information. Using the KURTOSIS option implies the SIMPLE
display option. This information is computed only if the DATA=
data set is a raw data set, and it is displayed by default if the PRINT
option is specified. The multivariate least squares kappa and the multivariate mean kappa are displayed only if you specify
METHOD=
WLS and the weight matrix is computed from an input raw data set. All measures of skewness and kurtosis are corrected for
the mean. Using the BIASKUR
option displays the biased values of univariate skewness and kurtosis.
-
LINESEARCH | LIS | SMETHOD | SM=i
LIS=i
SMETHOD=i
SM=i
-
specifies the line-search method for the
CONGRA, QUANEW, and NEWRAP
optimization techniques. See Fletcher (1980) for an introduction to line-search techniques. The value of i can be any integer between 1 and 8, inclusively; the default is i=2.
- 1
-
specifies a line-search method that needs the same number of function and gradient calls for cubic interpolation and cubic
extrapolation; this method is similar to one used by the Harwell subroutine library.
- 2
-
specifies a line-search method that needs more function calls than gradient calls for quadratic and cubic interpolation and
cubic extrapolation; this method is implemented as shown in Fletcher (1987) and can be modified to an exact line search by using the LSPRECISION=
option.
- 3
-
specifies a line-search method that needs the same number of function and gradient calls for cubic interpolation and cubic
extrapolation; this method is implemented as shown in Fletcher (1987) and can be modified to an exact line search by using the LSPRECISION=
option.
- 4
-
specifies a line-search method that needs the same number of function and gradient calls for stepwise extrapolation and cubic
interpolation.
- 5
-
specifies a line-search method that is a modified version of LIS=4.
-
LSPRECISION | LSP=r
LSP=r
SPRECISION=r
SP=r
-
specifies the degree of accuracy that should be obtained by the line-search algorithms LIS=
2 and LIS=
3.
Usually an imprecise line search is inexpensive and successful. For more difficult optimization problems, a more precise and
more expensive line search might be necessary (Fletcher 1980, p. 22). The second (default for NEWRAP, QUANEW, and CONGRA) and third line-search methods approach exact line search for
small LSPRECISION= values. If you have numerical problems, you should decrease the LSPRECISION= value to obtain a more precise
line search. The default LSPRECISION= values are displayed in the following table.
|
OMETHOD=
|
UPDATE=
|
LSP default
|
|
QUANEW
|
DBFGS, BFGS
|
r = 0.4
|
|
QUANEW
|
DDFP, DFP
|
r = 0.06
|
|
CONGRA
|
all
|
r = 0.1
|
|
NEWRAP
|
no update
|
r = 0.9
|
For more details, see Fletcher (1980, pp. 25–29).
-
MAXFUNC | MAXFU=i
-
specifies the maximum number i of function calls
in the optimization process. The default values are displayed in the following table.
|
OMETHOD=
|
MAXFUNC default
|
|
LEVMAR, NEWRAP, NRRIDG, TRUREG
|
i = 125
|
|
DBLDOG, QUANEW
|
i = 500
|
|
CONGRA
|
i = 1000
|
The default is used if you specify MAXFUNC=
0. The optimization can be terminated only after completing a full iteration. Therefore, the number of function calls that
is actually performed can exceed the number that is specified by the MAXFUNC=
option.
-
MAXITER=i <n>
MAXIT=i <n>
-
specifies the maximum number i of iterations
in the optimization process. Except for the iteratively reweighted least squares (IRLS) algorithm for the robust estimation
of model parameters, the default values are displayed in the following table.
|
OMETHOD=
|
MAXITER default
|
|
LEVMAR, NEWRAP, NRRIDG, TRUREG
|
i = 50
|
|
DBLDOG, QUANEW
|
i = 200
|
|
CONGRA
|
i = 400
|
The default maximum number of iterations for IRLS is 5000. The default value is used if you specify MAXITER=0 or if you omit
the MAXITER option.
The optional second value n is valid only for OMETHOD=QUANEW with nonlinear constraints. It specifies an upper bound n for the number of iterations of an algorithm and reduces the violation of nonlinear constraints at a starting point. The
default is n = 20. For example, specifying
maxiter= . 0
means that you do not want to exceed the default number of iterations during the main optimization process and that you want
to suppress the feasible point algorithm for nonlinear constraints.
-
MAXLEVERAGE=n
MAXLEV=n
-
specifies the maximum number of leverage observations to display in the output,
where n is between 1 and 9,999. The default MAXLEVERAGE= value is 30. The actual numbers of leverage observations in the output could
be smaller than the maximum. In general, PROC CALIS finds the number leverage points m and then adds the next 5 most leveraged observations in the output. The actual number of leverage observations shown in the
output is either m+5, the MAXLEVERAGE= value, or the number of observations in the data set, whichever is smaller.
-
MAXMISSPAT=n
-
specifies the maximum number of missing patterns to display in the output,
where n is between 1 and 9,999. The default MAXMISSPAT= value is 10 or the number of missing patterns in the data, whichever is smaller.
The number of missing patterns to display cannot exceed this MAXMISSPAT= value. This option is relevant only when there are
incomplete observations (with some missing values in the analysis variables) in the input raw data set and when you use METHOD=
FIML or METHOD=
LSFIML for estimation.
Because the number of missing patterns could be quite large, PROC CALIS displays a limited number of the most frequent missing
patterns in the output. The MAXMISSPAT= and the TMISSPAT=
options are used in determining the number of missing patterns to display. The missing patterns are ordered according to
the data proportions they account for, from the largest to the smallest. PROC CALIS displays a minimum number of the highest-frequency
missing patterns. This minimum number is the smallest among five, the actual number of missing patterns, and the MAXMISSPAT=
value. Then, PROC CALIS displays the subsequent high-frequency missing patterns if the data proportion accounted for by each
of these patterns is at least as large as the proportion threshold set by the TMISSPAT=
value (default at 0.05) until the total number of missing patterns displayed reaches the maximum set by the MAXMISSPAT= option.
-
MAXOUTLIER=n
MAXOUT=n
-
specifies the maximum number of outliers to display in the output,
where n is between 1 and 9,999. The default MAXOUTLIER= value is 30. The actual numbers of outliers displayed in the output could
be smaller than the maximum. In general, PROC CALIS finds the number outliers m and then adds the next 5 most outlying observations in the output. The actual number of outliers shown in the output is either
m+5, the MAXOUTLIER= value, or the number of observations in the data set, whichever is smaller.
-
MEANPATTERN=name
MEANPAT=name
-
specifies one of the built-in mean structures for the
data. The purpose of this option is to fit some commonly-used direct mean structures efficiently without the explicit use
of the MSTRUCT model specifications. With this option, the mean structures are defined internally in PROC CALIS. The following
names for the built-in mean structures are supported:
- EQMEANVEC
-
specifies the equality of mean vectors between multiple groups. That is, this option tests the null hypothesis that
where 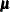 is a common mean vector for the k
is a common mean vector for the k 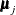 ’s (
’s (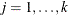 ). For example, if there are four variables in the analysis, the common
). For example, if there are four variables in the analysis, the common 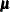 is defined as
is defined as
PROC CALIS denotes 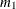 ,
, 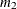 ,
, 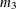 , and
, and 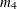 by
by _mean_1, _mean_2, _mean_3, and _mean_4, respectively.
If you use the COVPATTERN=
EQCOVMAT and MEANPATTERN= EQMEANVEC together in a maximum likelihood (METHOD=ML) analysis, you are testing a null hypothesis
of the same multivariate normal distribution for the groups.
If you use the MEANPATTERN=EQMEANVEC option for a single-group analysis, the parameters for the single group are still created
accordingly. However, the mean model for the single group contains only unconstrained parameters that would result in saturated
mean structures for the model.
- SATURATED
-
specifies a saturated mean structure model. This is the default mean structure pattern when the covariance structures are
specified by the COVPATTERN=
pattern and the mean structure analysis is invoked by MEANSTR
option. For example, if there are three variables in the analysis, 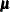 is defined as
is defined as
PROC CALIS denotes 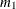 ,
, 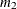 , and
, and 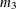 by
by _mean_1, _mean_2, and _mean_3, respectively.
- UNIFORM
-
specifies a mean vector with a uniform mean parameter. For example, if there are three variables in the analysis, the mean
pattern is:
PROC CALIS denotes the common mean parameter by _meanparm.
- ZERO
-
specifies a zero vector for the mean structures. For example, if there are four variables in the analysis, the mean pattern
generated by PROC CALIS is:
When you specify the mean structure model by means of the MEANPATTERN= option, you can define the set of variables in the
analysis by the VAR
statement (either within the scope of the PROC CALIS statement or the GROUP
statements). If the VAR statement is not used, PROC CALIS uses all numerical variables in the data sets.
Except for the EQMEANVEC pattern, all other built-in mean patterns are primarily designed for single-group analysis. However,
you can still use these mean pattern options for multiple-group situations. For example, consider the following three-group
analysis:
proc calis meanpattern=uniform;
group 1 / data=set1;
group 2 / data=set2;
group 3 / data=set3;
run;
In this specification, all three groups are fitted by the uniform mean pattern. However, there would be no constraints across
these groups. PROC CALIS generates a distinct mean parameter for each group: _meanparm_mdl1 for Group 1, _meanparm_mdl2 for Group 2, and _meanparm_mdl3 for Group 3. Similarly, the _mdlxx suffix, where xx represents the model number, is applied to the parameters defined by the SATURATED mean pattern in multiple-group situations.
You can also apply the MEANPATTERN= option partially to the groups in the analysis. For example, the following statements
apply the ZERO mean pattern to Group 1 and Group 2 only:
proc calis meanpattern=zero;
group 1 / data=set1;
group 2 / data=set2;
group 3 / data=set3;
model 3 / group=3;
path x1 ===> y3;
means x1 = mean_x1;
run;
Group 3 is fitted by Model 3, which is specified explicitly by a PATH model with a distinct mean parameter mean_x1.
If the EQMEANVEC pattern is specified instead, as shown in the following statements, the equality of mean vectors still holds
for Groups 1 and 2:
proc calis meanpattern=eqmeanvec;
group 1 / data=set1;
group 2 / data=set2;
group 3 / data=set3;
model 3 / group=3;
path x1 ===> y3;
means x1 = mean_x1;
run;
However, Group 3 has it own mean structures as specified in Model 3.
Use the COVPATTERN=
option if you also want to analyze some built-in covariance structures along with the mean structures. If you use the MEANPATTERN=
option but do not specify the COVPATTERN= option, a saturated covariance structure model (that is, COVPATTERN=SATURATED) is
assumed by default.
-
MEANSTR
-
invokes the analysis of mean structures. By default,
no mean structures are analyzed. You can specify the MEANSTR option in both the PROC CALIS and the MODEL
statements. When this option is specified in the PROC CALIS statement, it propagates to all models. When this option is specified
in the MODEL statement, it applies only to the local model. Except for the COSAN model, the MEANSTR option adds default mean
parameters to the model. For the COSAN model, the MEANSTR option adds null mean vectors to the model. Instead of using the
MEANSTR option to analyze the mean structures, you can specify the mean and the intercept parameters explicitly in the model
by some model specification statements. That is, you can specify the intercepts in the LINEQS
statement, the intercepts and means in the PATH
or the MEAN
statement, the _MEAN_ matrix in the MATRIX
statement, or the mean structure formula in the COSAN
statement. The explicit mean structure parameter specifications are useful when you need to constrain the mean parameters
or to create your own references of the parameters.
-
METHOD=name
MET=name
M=name
-
specifies the method of
parameter estimation. The default is METHOD=ML. You can specify the following names.
- ML | M | MAX
-
performs normal-theory
maximum likelihood parameter estimation. The ML method requires a nonsingular covariance or correlation matrix. For options
that provide more control of the standard error computation for METHOD=ML, see the INFORMATION=
and SE=
options.
- MLSB | ML(SB) | MLM
-
performs normal-theory maximum likelihood parameter estimation and the Satorra-Bentler
scale corrections on the chi-squares of the baseline and target models. Model fit statistics are then computed based on these
scaled chi-squares. This method also adjusts the computation of standard error estimates by using the sandwich formula proposed
by Satorra and Bentler (1994). In effect, the standard error estimates for METHOD=MLSB are the same as those obtained from METHOD=ML when you use the
SE=SBSW
option.
Because the chi-square statistics and standard error estimates for the MLSB method have been shown to have some desirable
statistical behavior even under the violation of multivariate normality assumption, the MLSB method is often referred to as
a robust maximum likelihood method. However, in the CALIS procedure, METHOD=MLSB is not the same! as METHOD=ML with the specification
of the ROBUST
option. The latter maximum likelihood method achieves the robustness by case-level weighting of the observations during iterative
estimation. However, the MLSB method does not use case-level weighting at all. Instead, it can be viewed as a kind of postestimation
adjustment of the chi-squares and standard error estimates.
The MLSB method requires raw input data sets. If you do not provide raw data, the estimation results of MLSB are the same
as those obtained from METHOD=ML. For options that provide more control of the chi-square correction and standard error computation
for METHOD=MLSB, see the INFORMATION=
, SBNTW=
, and SE=
options.
- FIML
-
performs full information maximum likelihood (FIML) or direct maximum likelihood
parameter estimation for data that have missing values. This method assumes raw input data sets. When there are no missing
values in the analysis, the FIML method yields the same estimates as those from using the regular maximum likelihood (METHOD=ML)
method with VARDEF=
N.
For METHOD=FIML, the observed information matrix, rather than the expected information matrix, is the default for computing
standard error estimates. The use of the observed information matrix has been proved to produce better standard error estimates
under the missing at random condition. However, you can specify INFORMATION=EXPECTED
to overwrite the default.
Because the FIML method recomputes the mean estimates iteratively during estimation, it must intrinsically analyze the mean
structures of models. If you do not specify the MEANSTR
option or any mean parameters for your models (which is not required for using the FIML method), PROC CALIS assumes saturated
mean structures for models. However, when computing fit statistics, these saturated mean structures would be ignored as if
they were never modeled. If you do specify the MEANSTR
option or any mean parameters for your models, these mean structures would be taken into account when computing fit statistics.
- GLS | G
-
performs generalized least squares parameter estimation.
If no INWGT=
data set is specified, the GLS method uses the inverse sample covariance or correlation matrix as the weight matrix 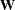 . Therefore, METHOD=GLS requires a nonsingular covariance or correlation matrix. For more control of the standard error computation
for METHOD=GLS, see the INFORMATION=
option.
. Therefore, METHOD=GLS requires a nonsingular covariance or correlation matrix. For more control of the standard error computation
for METHOD=GLS, see the INFORMATION=
option.
- WLS | W | ADF
-
performs weighted least squares
parameter estimation. If no INWGT=
data set is specified, the WLS method uses the inverse matrix of estimated asymptotic covariances of the sample covariance
or correlation matrix as the weight matrix 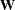 . In this case, the WLS estimation method is equivalent to Browne’s asymptotically
distribution-free estimation (Browne 1982, 1984). The WLS method requires a nonsingular weight matrix.
. In this case, the WLS estimation method is equivalent to Browne’s asymptotically
distribution-free estimation (Browne 1982, 1984). The WLS method requires a nonsingular weight matrix.
- DWLS | D
-
performs diagonally weighted
least squares parameter estimation. If no INWGT=
data set is specified, the DWLS method uses the inverse diagonal matrix of asymptotic variances of the input sample covariance
or correlation matrix as the weight matrix 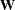 . The DWLS method requires a nonsingular diagonal weight matrix.
. The DWLS method requires a nonsingular diagonal weight matrix.
- ULS | LS | U
-
performs unweighted least squares parameter estimation.
- LSML | LSM | LSMAX
-
performs unweighted least squares followed by normal-theory maximum-likelihood parameter estimation.
- LSMLSB | LSML(SB) | LSMLM
-
performs unweighted least squares followed by normal-theory maximum likelihood parameter estimation. It also computes the
Satorra-Bentler scaled chi-squares of the baseline and target models under maximum likelihood estimation. The standard errors
of maximum likelihood estimates are based on the sandwich formula proposed by Satorra and Bentler (1994).
- LSFIML
-
performs unweighted least squares followed by full information maximum-likelihood parameter estimation.
- LSGLS | LSG
-
performs unweighted least squares followed by generalized least squares parameter estimation.
- LSWLS | LSW | LSADF
-
performs unweighted least squares followed by weighted least squares parameter estimation.
- LSDWLS | LSD
-
performs unweighted least squares followed by diagonally weighted least squares parameter estimation.
- NONE | NO
-
uses no estimation method. This option is suitable for checking the validity of the input information and for displaying the
model matrices and initial values.
-
MODIFICATION
MOD
-
computes and displays
Lagrange multiplier (LM) test indices
for constant parameter constraints, equality parameter constraints, and active boundary constraints, as well as univariate
and multivariate Wald test indices. The modification indices are not computed in the case of unweighted or diagonally weighted
least squares estimation.
The Lagrange multiplier test (Bentler 1986; Lee 1985; Buse 1982) provides an estimate of the 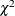 reduction that results from dropping the constraint. For constant parameter constraints and active boundary constraints,
the approximate change of the parameter value is displayed also. You can use this value to obtain an initial value if the
parameter is allowed to vary in a modified model. See the section Modification Indices for more information.
reduction that results from dropping the constraint. For constant parameter constraints and active boundary constraints,
the approximate change of the parameter value is displayed also. You can use this value to obtain an initial value if the
parameter is allowed to vary in a modified model. See the section Modification Indices for more information.
Relying solely on the LM tests to modify your model can lead to unreliable models that capitalize purely on sampling errors.
See MacCallum, Roznowski, and Necowitz (1992) for the use of LM tests.
-
MSINGULAR=r
MSING=r
-
specifies a relative singularity
criterion r (r > 0) for the inversion of the information matrix, which is needed to compute the covariance matrix. If you do not specify
the SINGULAR=
option, the default value for r or MSING= is 1E–12; otherwise, the default value is 1E–4  SING, where SING is the specified SINGULAR=
value.
SING, where SING is the specified SINGULAR=
value.
When inverting the information matrix, the following singularity criterion is used for the diagonal pivot 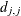 of the matrix:
of the matrix:
where ASING and VSING are the specified values of the ASINGULAR=
and VSINGULAR=
options, respectively, and 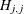 is the jth diagonal element of the information matrix. Note that in many cases a normalized matrix
is the jth diagonal element of the information matrix. Note that in many cases a normalized matrix 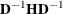 is decomposed (where
is decomposed (where 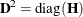 ), and the singularity criteria are modified correspondingly.
), and the singularity criteria are modified correspondingly.
-
NOADJDF
-
turns off the automatic adjustment of degrees of freedom when there
are active constraints in the analysis. When the adjustment is in effect, most fit statistics and the associated probability
levels will be affected. This option should be used when you believe that the active constraints observed in the current sample
will have little chance to occur in repeated sampling. See the section Adjustment of Degrees of Freedom for more discussion on the issue.
-
NOBS=nobs
-
specifies the number of observations.
If the DATA=
input data set is a raw data set, nobs is defined by default to be the number of observations in the raw data set. The NOBS= and EDF=
options override this default definition. You can use the RDF=
option to modify the nobs specification. If the DATA=
input data set contains a covariance, correlation, or scalar product matrix, you can specify the number of observations either
by using the NOBS=, EDF=
, and RDF=
options in the PROC CALIS statement or by including a _TYPE_='N' observation in the DATA=
input data set.
-
NOINDEXTYPE
-
disables the display of index types in the fit summary table.
-
NOMEANSTR
-
deactivates the inherited MEANSTR
option for the analysis of mean structures.
You can specify the NOMEANSTR option in both the PROC CALIS and the MODEL
statements. When this option is specified in the PROC CALIS statement, it does not have any apparent effect because by default
the mean structures are not analyzed. When this option is specified in the MODEL statement, it deactivates the inherited MEANSTR
option from the PROC CALIS statement. In other words, this option is mainly used for resetting the default behavior in the
local model that is specified within the scope of a particular MODEL statement. If you specify both the MEANSTR and NOMEANSTR
options in the same statement, the NOMEANSTR option is ignored.
Caution: This option does not remove the mean structure specifications from the model. It only deactivates the MEANSTR option inherited
from the PROC CALIS statement. The mean structures of the model are analyzed as long as there are mean structure specifications
in the model (for example, when you specify the means or intercepts in any of the main
or subsidiary
model specification statements).
-
NOMISSPAT
-
suppresses the display of the analytic results of the missing patterns.
This option is relevant only when there are incomplete observations (with some missing values in the analysis variables) in
the input raw data set and when you use METHOD=
FIML or METHOD=
LSFIML for estimation.
-
NOMOD
-
suppresses the computation of modification indices. The NOMOD option is
useful in connection with the PALL
option because it saves computing time.
-
NOORDERSPEC
-
prints the model results in the order they appear in the input specifications.
This is the default printing behavior. In contrast, the ORDERSPEC
option arranges the model results by the types of parameters. You can specify the NOORDERSPEC option in both the PROC CALIS
and the MODEL
statements. When this option is specified in the PROC CALIS statement, it does not have any apparent effect because by default
the model results display in the same order as that in the input specifications. When this option is specified in the MODEL
statement, it deactivates the inherited ORDERSPEC option from the PROC CALIS statement. In other words, this option is mainly
used for resetting the default behavior in the local model that is specified within the scope of a particular MODEL statement.
If you specify both the ORDERSPEC and NOORDERSPEC options in the same statement, the NOORDERSPEC option is ignored.
-
NOPARMNAME
-
suppresses the printing of parameter names in the model results. The
default is to print the parameter names. You can specify the NOPARMNAME option in both the PROC CALIS and the MODEL
statements. When this option is specified in the PROC CALIS statement, it propagates to all models. When this option is specified
in the MODEL statement, it applies only to the local model.
-
NOPRINT
NOP
-
suppresses the displayed output. Note that this option
temporarily disables the Output Delivery System (ODS). See Chapter 20: Using the Output Delivery System, for more information.
-
NOSTAND
-
suppresses the printing of standardized results. The default is
to print the standardized results.
-
NOSTDERR
NOSE
-
suppresses the printing of the standard error estimates.
Standard errors are not computed for unweighted least squares (ULS) or diagonally weighted least squares (DWLS) estimation.
In general, standard errors are computed even if the STDERR
display option is not used (for file output). You can specify the NOSTDERR option in both the PROC CALIS and the MODEL
statements. When this option is specified in the PROC CALIS statement, it propagates to all models. When this option is specified
in the MODEL statement, it applies only to the local model.
-
OMETHOD=name
OM=name
TECHNIQUE=name
TECH=name
-
specifies the optimization method or technique. Because there is no single nonlinear optimization algorithm available that
is clearly superior (in terms of stability, speed, and memory) for all applications, different types of optimization methods
or techniques are provided in the CALIS procedure.
The optimization method or technique is specified by using one of the following names in the OMETHOD= option:
- CONGRA | CG
-
chooses one of four
different conjugate-gradient optimization algorithms, which can be more precisely defined with the UPDATE=
option and modified with the LINESEARCH=
option. The conjugate-gradient techniques need only 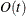 memory compared to the
memory compared to the 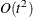 memory for the other three techniques, where t is the number of parameters. On the other hand, the conjugate-gradient techniques are significantly slower than other optimization
techniques and should be used only when memory is insufficient for more efficient techniques. When you choose this option,
UPDATE=
PB by default. This is the default optimization technique if there are more than 999 parameters to estimate.
memory for the other three techniques, where t is the number of parameters. On the other hand, the conjugate-gradient techniques are significantly slower than other optimization
techniques and should be used only when memory is insufficient for more efficient techniques. When you choose this option,
UPDATE=
PB by default. This is the default optimization technique if there are more than 999 parameters to estimate.
- DBLDOG | DD
-
performs a version of
double dogleg optimization, which uses the gradient to update an approximation of the Cholesky factor of the Hessian. This
technique is, in many aspects, very similar to the dual quasi-Newton method, but it does not use line search. The implementation
is based on Dennis and Mei (1979) and (Gay 1983).
- LEVMAR | LM | MARQUARDT
-
performs a highly stable (but for large problems, memory- and time-consuming) Levenberg-Marquardt
optimization technique, a slightly improved variant of the (Moré 1978) implementation. This is the default optimization technique for estimation methods other than the FIML if there are fewer
than 500 parameters to estimate.
- NEWRAP | NRA
-
performs a usually stable (but for large problems,
memory- and time-consuming) Newton-Raphson optimization technique. The algorithm combines a line-search algorithm with ridging,
and it can be modified with the LINESEARCH=
option.
- NRRIDG | NRR | NR | NEWTON
-
performs a usually
stable (but for large problems, memory- and time-consuming) Newton-Raphson optimization technique. This algorithm does not
perform a line search. Since OMETHOD=NRRIDG uses an orthogonal decomposition of the approximate Hessian, each iteration of
OMETHOD=NRRIDG can be slower than that of OMETHOD=NEWRAP, which works with Cholesky decomposition. However, usually OMETHOD=NRRIDG
needs fewer iterations than OMETHOD=NEWRAP. The NRRIDG technique is the default optimization for the FIML estimation if there
are fewer than 500 parameters to estimate.
- QUANEW | QN
-
chooses one of four different quasi-Newton optimization algorithms that can be more precisely
defined with the UPDATE=
option and modified with the LINESEARCH=
option. If boundary constraints are used, these techniques sometimes converge slowly. When you choose this option, UPDATE=
DBFGS by default. If nonlinear constraints are specified in the NLINCON
statement, a modification of Powell’s VMCWD algorithm (Powell 1982a, 1982b) is used, which is a sequential quadratic programming (SQP) method. This algorithm can be modified by specifying VERSION=1,
which replaces the update of the Lagrange multiplier estimate vector 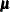 to the original update of Powell (1978b, 1978a) that is used in the VF02AD algorithm. This can be helpful for applications with linearly dependent active constraints. The
QUANEW technique is the default optimization technique if there are nonlinear constraints specified or if there are more than
499 and fewer than 1,000 parameters to estimate. The QUANEW algorithm uses only first-order derivatives of the objective function
and, if available, of the nonlinear constraint functions.
to the original update of Powell (1978b, 1978a) that is used in the VF02AD algorithm. This can be helpful for applications with linearly dependent active constraints. The
QUANEW technique is the default optimization technique if there are nonlinear constraints specified or if there are more than
499 and fewer than 1,000 parameters to estimate. The QUANEW algorithm uses only first-order derivatives of the objective function
and, if available, of the nonlinear constraint functions.
- TRUREG | TR
-
performs a usually very stable (but
for large problems, memory- and time-consuming) trust-region optimization technique. The algorithm is implemented similar
to Gay (1983) and Moré and Sorensen (1983).
- NONE | NO
-
does not perform any optimization. This option is similar to METHOD=
NONE, but OMETHOD=NONE also computes and displays residuals and goodness-of-fit statistics. If you specify METHOD=
ML, METHOD=
LSML, METHOD=
GLS, METHOD=
LSGLS, METHOD=
WLS, or METHOD=
LSWLS, this option enables computing and displaying (if the display options are specified) of the standard error estimates
and modification indices corresponding to the input parameter estimates.
For fewer than 500 parameters (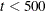 ), OMETHOD=NRRIDG (Newton-Raphson Ridge) is the default optimization technique for the FIML estimation, and OMETHOD=LEVMAR
(Levenberg-Marquardt) is the default optimization technique for the all other estimation methods. For
), OMETHOD=NRRIDG (Newton-Raphson Ridge) is the default optimization technique for the FIML estimation, and OMETHOD=LEVMAR
(Levenberg-Marquardt) is the default optimization technique for the all other estimation methods. For 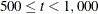 , OMETHOD=
QUANEW (quasi-Newton) is the default method, and for
, OMETHOD=
QUANEW (quasi-Newton) is the default method, and for 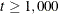 , OMETHOD=
CONGRA (conjugate gradient) is the default method. Each optimization method or technique can be modified in various ways.
See the section Use of Optimization Techniques for more details.
, OMETHOD=
CONGRA (conjugate gradient) is the default method. Each optimization method or technique can be modified in various ways.
See the section Use of Optimization Techniques for more details.
-
ORDERALL
-
prints the model and group results in the order of the model or group numbers,
starting from the smallest number. It also arrange some model results by the parameter types. In effect, this option turns
on the ORDERGROUPS
, ORDERMODELS
, and ORDERSPEC
options. The ORDERALL is not a default option. By default, the printing of the results follow the order of the input specifications.
-
ORDERGROUPS
ORDERG
-
prints the group results in the order of the group numbers,
starting from the smallest number. The default behavior, however, is to print the group results in the order they appear in
the input specifications.
-
ORDERMODELS
ORDERMO
-
prints the model results in the order of the model numbers,
starting from the smallest number. The default behavior, however, is to print the model results in the order they appear in
the input specifications.
-
ORDERSPEC
-
arranges some model results by the types of parameters.
The default behavior, however, is to print the results in the order they appear in the input specifications. You can specify
the ORDERSPEC option in both the PROC CALIS and the MODEL
statements. When this option is specified in the PROC CALIS statement, it propagates to all models. When this option is specified
in the MODEL statement, it applies only to the local model.
-
OUTEST=SAS-data-set
-
creates an output data set that contains
the parameter estimates, their gradient, Hessian matrix, and boundary and linear constraints. For METHOD=
ML, METHOD=
GLS, and METHOD=
WLS, the OUTEST= data set also contains the information matrix, the approximate covariance matrix of the parameter estimates
((generalized) inverse of information matrix), and approximate standard errors. If linear or nonlinear equality or active
inequality constraints are present, the Lagrange multiplier estimates of the active constraints, the projected Hessian, and
the Hessian of the Lagrange function are written to the data set.
See the section OUTEST= Data Set for a description of the OUTEST= data set. If you want to create a SAS data set in a permanent library, you must specify
a two-level name. For more information about permanent libraries and SAS data sets, see
SAS Language Reference: Concepts.
-
OUTFIT=SAS-data-set
-
creates an output data set that contains the values of the fit indices.
See the section OUTFIT= Data Set for details.
-
OUTMODEL=SAS-data-set
OUTRAM=SAS-data-set
-
creates an output data set that contains
the model information for the analysis, the parameter estimates, and their standard errors. An OUTMODEL= data set can be used
as an input INMODEL=
data set in a subsequent analysis by PROC CALIS. If you want to create a SAS data set in a permanent library, you must specify
a two-level name. For more information about permanent libraries and SAS data sets, see
SAS Language Reference: Concepts.
-
OUTSTAT=SAS-data-set
-
creates an output data set that contains the BY
group variables, the analyzed covariance or correlation matrices, and the predicted and residual covariance or correlation
matrices of the analysis. You can specify the correlation or covariance matrix in an OUTSTAT= data set as an input DATA=
data set in a subsequent analysis by PROC CALIS. See the section OUTSTAT= Data Set for a description of the OUTSTAT= data set. If the model contains latent variables, this data set also contains the predicted
covariances between latent and manifest variables and the latent variable score regression coefficients (see the
PLATCOV option
). If the FACTOR
statement is used, the OUTSTAT= data set also contains the rotated and unrotated factor loadings, the unique variances, the
matrix of factor correlations, the transformation matrix of the rotation, and the matrix of standardized factor loadings.
You can use the latent variable score regression coefficients with PROC SCORE to compute factor scores.
If you want to create a SAS data set in a permanent library, you must specify a two-level name. For more information about
permanent libraries and SAS data sets, see
SAS Language Reference: Concepts.
-
OUTWGT=SAS-data-set
OUTWEIGHT=SAS-data-set
-
creates an output data set that contains the elements of the
weight matrix 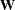 or the its inverse
or the its inverse 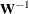 used in the estimation process. The inverse of the weight matrix is output only when you specify an INWGT= data set with
the INWGT=
and INWGTINV
options (or the INWGT(INV)=
option alone) in the same analysis. As a result, the entries in the INWGT= and OUTWGT= data sets are consistent. In other
situations where the weight matrix is computed by the procedure or obtained from the OUTWGT= data set without the INWGTINV
option, the weight matrix is output in the OUTWGT= data set. Furthermore, if the weight matrix is computed by the procedure,
the OUTWGT= data set contains the elements of the weight matrix on which the WRIDGE=
and the WPENALTY=
options are applied.
used in the estimation process. The inverse of the weight matrix is output only when you specify an INWGT= data set with
the INWGT=
and INWGTINV
options (or the INWGT(INV)=
option alone) in the same analysis. As a result, the entries in the INWGT= and OUTWGT= data sets are consistent. In other
situations where the weight matrix is computed by the procedure or obtained from the OUTWGT= data set without the INWGTINV
option, the weight matrix is output in the OUTWGT= data set. Furthermore, if the weight matrix is computed by the procedure,
the OUTWGT= data set contains the elements of the weight matrix on which the WRIDGE=
and the WPENALTY=
options are applied.
You cannot create an OUTWGT= data set with an unweighted least squares or maximum likelihood estimation. The weight matrix
is defined only in the GLS, WLS (ADF), or DWLS fit function. An OUTWGT= data set can be used as an input INWGT=
data set in a subsequent analysis by PROC CALIS. See the section OUTWGT= Data Set for the description of the OUTWGT= data set. If you want to create a SAS data set in a permanent library, you must specify
a two-level name. For more information about permanent libraries and SAS data sets, see
SAS Language Reference: Concepts.
-
PALL
ALL
-
displays all optional output
except the output generated by the PCOVES
and PDETERM
options.
Caution: The PALL option includes the very expensive computation of the modification indices. If you do not really need modification
indices, you can save computing time by specifying the NOMOD
option in addition to the PALL option.
-
PARMNAME
-
prints the parameter names in the model results.
This is the default printing behavior. In contrast, the NOPARMNAME
option suppresses the printing of the parameter names in the model results. You can specify the PARMNAME option in both the
PROC CALIS and the MODEL
statements. When this option is specified in the PROC CALIS statement, it does not have any apparent effect because by default
model results show the parameter names. When this option is specified in the MODEL statement, it deactivates the inherited
NOPARMNAME option from the PROC CALIS statement. In other words, this option is mainly used for resetting the default behavior
in the local model that is specified within the scope of a particular MODEL statement. If you specify both the PARMNAME and
NOPARMNAME options in the same statement, the PARMNAME option is ignored.
-
PCORR
CORR
-
displays the covariance or
correlation matrix that is analyzed and the predicted model covariance or correlation matrix.
-
PCOVES
PCE
-
displays the following:
The covariance matrix of the parameter estimates is not computed for estimation methods ULS and DWLS. This displayed output
is not included in the output generated by the PALL
option.
-
PDETERM
PDE
-
displays three coefficients
of determination: the determination of all equations (DETAE), the determination of the structural equations (DETSE), and the
determination of the manifest variable equations (DETMV). These determination coefficients are intended to be global means
of the squared multiple correlations for different subsets of model equations and variables. The coefficients are displayed
only when you specify a FACTOR, LINEQS, LISMOD, PATH, or RAM model, but they are displayed for all five estimation methods:
ULS, GLS, ML, WLS, and DWLS.
You can use the STRUCTEQ
statement to define which equations are structural equations. If you do not use the STRUCTEQ
statement, PROC CALIS uses its own default definition to identify structural equations.
The term "structural equation" is not defined in a unique way.
The LISREL program defines the structural equations by the user-defined BETA matrix. In PROC CALIS, the default definition
of a structural equation is an equation that has a dependent left-side variable that appears at least once on the right side
of another equation, or an equation that has at least one right-side variable that appears at the left side of another equation.
Therefore, PROC CALIS sometimes identifies more equations as structural equations than the LISREL program does.
-
PESTIM
PES
-
displays the parameter
estimates. In some cases, this includes displaying the standard errors and t values.
-
PIN
PIN
-
displays the model specification with initial estimates and the
vector of initial values.
-
PLATCOV
PLATMOM
PLC
-
displays the following:
-
the estimates of the covariances among the latent variables
-
the estimates of the covariances between latent and manifest variables
-
the estimates of the latent variable means for mean structure analysis
-
the latent variable score regression coefficients
The estimated covariances between latent and manifest variables and the latent variable score regression coefficients are
written to the OUTSTAT=
data set. You can use the score coefficients with
PROC SCORE to compute factor scores.
-
PLOTS<=plot-request>
PLOT<=(plot-request < …plot-request>)>
-
specifies the ODS Graphics plots. When you specify only one plot-request, you can omit the parentheses around the plot-request. For example:
PLOTS=ALL PLOTS=RESIDUALS PLOTS=(PP RESBYPRED QQ)
ODS Graphics must be enabled before plots can be requested. For example:
ods graphics on;
proc calis plots;
path y <=== x,
y <=== z;
run;
ods graphics off;
For more information about enabling and disabling ODS Graphics, see the section Enabling and Disabling ODS Graphics in Chapter 21: Statistical Graphics Using ODS.
You can specify the following plot-requests:
- ALL
-
displays all plots.
- CASERESID | CASERESIDUAL | CASERESIDUALS
-
displays all the case-level ODS Graphics plots enabled by the following plot-requests: CRESHIST, PP, QQ, RESBYLEV, and RESBYPRED. This option requires raw data input.
- CRESHIST | CRESIDUALHISTOGRAM
-
produces the ODS Graphics plot CaseResidualHistogram, which displays the distribution of the case-level (observation-level)
residuals in the form of a histogram, where residuals are measured in terms of M-distances. This option requires raw data
input.
- NONE
-
suppresses ODS Graphics plots.
- PATHDIAGRAM
-
produces the ODS Graphics plot PathDiagram, which display the path diagram for the unstandardized solution. For options that
control and customize path diagrams, see the PATHDIAGRAM
statement.
- PP | PPPLOT
-
produces the ODS Graphics plot ResPercentileByExpPercentile, which plots the observed percentiles of the residual M-distances
against the theoretical percentiles. This plot is useful for showing departures from the theoretical distribution in terms
of percentiles, and it is especially sensitive to departures in the middle region of the distribution. This option requires
raw data input.
- QQ | QQPLOT
-
produces the ODS Graphics plot ResidualByQuantile, which plots the residual M-distances (observed quantiles) against the theoretical
quantiles. This plot is useful for showing departures from the theoretical distribution in terms of quantiles, and it is especially
sensitive to departures at the upper tail of the distribution. This option requires raw data input.
- RESBYLEV | RESIDUALBYLEVERAGE
-
produces the ODS Graphics plot ResidualByLeverage, which plots the residual M-distances against the leverage M-distances.
This plot is useful for showing outliers and leverage observations graphically. See the ALPHAOUT=
and ALPHALEV=
options for detection criteria of outliers and leverage observations. This option requires raw data input.
- RESBYPRED | RESONFIT | RESIDUALBYPREDICTED | RESIDUALONFIT<(VAR= var-list)>
-
produces the ODS Graphics plot ResidualByPredicted, which plots the residuals against the predicted values of the dependent
observed variables in the model. You can restrict the set of dependent variables to display by specifying var-list in the VAR= option. If var-list is not specified in the VAR= option, plots for all dependent observed variables are displayed. The residual on fit plots
are useful for detecting nonlinear relationships in the model. If the relationships are linear and the residual variance is
homoscedastic, the residuals should not show systematic pattern with the predicted values. This option requires raw data input.
- RESIDUAL | RESIDUALS
-
produces the ODS Graphics plot for the histogram of residuals in covariances and means rather than the case-level residuals.
With this ODS Graphics plot, the nongraphical (legacy) output for the bar chart of residual tallies is redundant and therefore
is suppressed. To display this bar chart together with the ODS Graphics for residual histogram, you must use the RESIDUAL(TALLY)
option in the PROC CALIS statement. This option does not require raw data input.
-
PRIMAT
PMAT
-
displays parameter estimates, approximate standard errors, and t
values in matrix form if you specify the analysis model using the RAM
or LINEQS
statement.
-
PRINT
PRI
-
adds the options KURTOSIS
, RESIDUAL
, PLATCOV
,
and TOTEFF
to the default output.
-
PSHORT
SHORT
PSH
-
excludes the output produced by the PINITIAL
, SIMPLE
, and STDERR
options
from the default output.
-
PSUMMARY | SUMMARY | PSUM
SUMMARY
PSUM
-
displays the fit assessment table only.
-
PWEIGHT
PW
-
displays the weight matrix 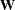 used in the estimation. The weight matrix is displayed after the WRIDGE=
and the WPENALTY=
options are applied to it. However, if you specify an INWGT= data set by the INWGT=
and INWGTINV
options (or the INWGT(INV)=
option alone) in the same analysis, this option displays the elements of the inverse of the weight matrix.
used in the estimation. The weight matrix is displayed after the WRIDGE=
and the WPENALTY=
options are applied to it. However, if you specify an INWGT= data set by the INWGT=
and INWGTINV
options (or the INWGT(INV)=
option alone) in the same analysis, this option displays the elements of the inverse of the weight matrix.
-
RADIUS=r
-
is an alias for the INSTEP=
option for Levenberg-Marquardt minimization.
-
RANDOM=i
-
specifies a positive integer as a seed value for
the pseudo-random number generator to generate initial values for the parameter estimates for which no other initial value
assignments in the model definitions are made. Except for the parameters in the diagonal locations of the central matrices
in the model, the initial values are set to random numbers in the range 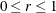 . The values for parameters in the diagonals of the central matrices are random numbers multiplied by 10 or 100. See the section
Initial Estimates for more information.
. The values for parameters in the diagonals of the central matrices are random numbers multiplied by 10 or 100. See the section
Initial Estimates for more information.
-
RDF=n
DFR=n
-
makes the effective number of
observations the actual number of observations minus the RDF= value. The degree of freedom for the intercept should not be
included in the RDF= option. If you use PROC CALIS to compute a regression model, you can specify RDF= number-of-regressor-variables to get approximate standard errors equal to those computed by PROC REG.
-
READADDPARM
READADD
-
inputs the generated default parameters
(for example, observations with _TYPE_=ADDPCOV, ADDMEAN, or ADDPVAR) in the INMODEL=
data set as if they were part of the original model specification. Typically, these default parameters in the INMODEL=
data set were generated automatically by PROC CALIS in a previous analysis and stored in an OUTMODEL=
data set, which is then used as the INMODEL= data set in a new run of PROC CALIS. By default, PROC CALIS does not input the
observations for default parameters in the INMODEL= data set. In most applications, you do not need to specify this option
because PROC CALIS is able to generate a new set of default parameters that are appropriate to the new situation after it
reads in the INMODEL= data set. Undistinguished uses of the READADDPARM option might lead to unintended constraints on the
default parameters.
-
RESIDUAL <(TALLY | TALLIES)> <= NORM | VARSTAND | ASYSTAND>
RES <(TALLY | TALLIES)> <= NORM | VARSTAND | ASYSTAND>
-
displays the raw and
normalized residual covariance matrix, the rank order of the largest residuals, and a bar chart of the residual tallies. If
mean structures are modeled, mean residuals are also displayed and ranked.
For raw data input, this option also displays tables for case-level (observation-level) residual analysis, including outlier
and leverage detections and departures of residuals from the theoretical residual distributions. To set the criterion for
detecting outliers, use the ALPHAOUT=
option. To set the criterion for leverage observations, use the ALPHALEV=
option. Case-level residual analysis is not available when you specify METHOD=FIML.
For the covariance and mean residuals, three types of normalized or standardized residual matrices can be chosen with the
RESIDUAL= specification.
- NORM
-
normalized residuals
- VARSTAND
-
variance standardized residuals
- ASYSTAND
-
asymptotically standardized residuals
When ODS Graphics plots
of covariance and mean residuals are also requested, the bar charts of residual tallies are suppressed. They are replaced
with high quality graphical histograms showing residual distributions. If you still want to display the bar charts in this
situation, use the RESIDUAL(TALLY) or RESIDUAL(TALLY)= option.
The RESIDUAL option is also enabled by the PRINT
option. See the section Assessment of Fit for more details about the definitions of residuals.
-
RIDGE<=r>
-
defines a ridge factor r for the
diagonal of the covariance or correlation matrix 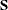 that is analyzed. The matrix
that is analyzed. The matrix 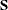 is transformed to:
is transformed to:
If you do not specify r in the RIDGE option, PROC CALIS tries to ridge the covariance or correlation matrix 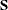 so that the smallest eigenvalue is about
so that the smallest eigenvalue is about 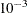 . Because the weight matrix in the GLS method is the same as the observed covariance or correlation matrix, the RIDGE= option
also applies to the weight matrix for the GLS estimation, unless you input the weight matrix by the INWGT=
option.
. Because the weight matrix in the GLS method is the same as the observed covariance or correlation matrix, the RIDGE= option
also applies to the weight matrix for the GLS estimation, unless you input the weight matrix by the INWGT=
option.
Caution: The covariance or correlation matrix in the OUTSTAT=
output data set does not contain the ridged diagonal.
-
ROBITER=i
ROBUSTITER=i
-
specifies the maximum number i of iterations
for the iteratively reweighted least squares (IRLS) method to compute the robust mean and covariance matrices with the two-stage
robust estimation. This option is relevant only with the use of the ROBUST=
option and with raw data input. The default value is 5,000.
You can also specify this option in the GROUP
statement so that different groups can use different ROBITER= values. Notice that the ROBITER= option does not specify the
maximum number of iterations for the IRLS algorithm used in the direct robust estimation or in the second stage of the two-stage
robust estimation. You can specify the MAXITER=
option for this purpose.
-
ROBPHI=r
ROBUSTPHI=r
-
sets the tuning parameter r (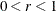 ) for the robust estimation method
that you specify using the ROBUST=
option. The ROBPHI= value controls the criterion for downweighting observations. This value indicates approximately the proportion
of observations that would receive weights less than 1 (that is, would be downweighted) according to certain theoretical distributions.
The larger the ROBPHI= value, the more observations are downweighted (that is, with weights less than 1). The default value
is 0.05.
) for the robust estimation method
that you specify using the ROBUST=
option. The ROBPHI= value controls the criterion for downweighting observations. This value indicates approximately the proportion
of observations that would receive weights less than 1 (that is, would be downweighted) according to certain theoretical distributions.
The larger the ROBPHI= value, the more observations are downweighted (that is, with weights less than 1). The default value
is 0.05.
You can also specify this option in the GROUP
statement so that different groups can use different ROBPHI= values for the tuning parameters.
-
ROBUST <=name>
ROB <=name>
-
invokes the robust estimation method that downweights the outliers in estimation.
You can use the ROBUST option only in conjunction with the ML method (METHOD=
ML). More accurately, the robust estimation is done by using the iteratively reweighted least squares (IRLS) method under
the normal distribution assumption. The model fit of robust estimation is evaluated with the ML discrepancy function.
You must provide raw data input for the robust estimation method to work. With the robust method, the Huber weights are applied
to the observations so that outliers are downweighted during estimation. See the section Robust Estimation for details.
You can request the three different types of robust methods by using one of the following names:
- RESIDUAL | DIRECT | RESID | RES <(E)>
-
specifies a direct robust method that downweights observations with large residuals during the iterative estimation of the
model. This method treats the disturbances (the error terms of endogenous latent factors) as errors or residuals (hence the
keyword E) in the associated factor model when computing residual M-distances and factor scores during the robust estimation. The (E)specification is irrelevant if there are no endogenous latent factors in the model. This is the default robust method.
- RESIDUAL | DIRECT | RESID | RES (F)
-
specifies a direct robust method that downweights observations with large estimated residuals during the iterative estimation
of the model. Unlike the (E)method, this method treats the disturbances (the error terms of endogenous latent factors) as factors (hence the keyword F) in the associated factor model when computing residual M-distances and factor scores during the robust estimation. The (F)specification is irrelevant if there are no endogenous latent factors in the model.
- SAT | TWOSTAGE | UNSTRUCT | UNS
-
specifies a two-stage robust method that downweights the observations with large M-distances in all observed variable dimensions
when computing the covariance matrix and mean vector from the input raw data. As a results, this option produces a robust
covariance matrix and a mean vector for a subsequent model estimation where no reweighting would be applied at the observational
level. Hence, this is a two-stage method that applies weights only in the first stage for computing the robust covariance
and mean matrices. This is in contrast with the RES(E) or RES(F) option, where weighting and reweighting of observations are applied directly during model estimation.
For details about these robust methods, see the section Robust Estimation.
To control the proportion of the observations that are downweighted during the robust estimation, you can specify the value
of the tuning parameter 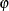 , which is between 0 and 1, by using the ROBPHI=
option. Approximately,
, which is between 0 and 1, by using the ROBPHI=
option. Approximately,  of observations would receive weights less than 1 according to certain theoretical distributions. By default, the value of
the tuning parameter
of observations would receive weights less than 1 according to certain theoretical distributions. By default, the value of
the tuning parameter  is set to 0.05 for all robust methods in PROC CALIS.
is set to 0.05 for all robust methods in PROC CALIS.
By default, the robust method uses a maximum of 5,000 iterations to obtain parameter convergence through the IRLS algorithm.
You can override this default maximum number of iterations by specifying the ROBITER=
option. The default relative parameter convergence criterion for the robust method is 1E–8. See the XCONV=
option for the mathematical definition of this criterion and for information about overriding the default convergence criterion.
Because all robust methods reweight the observations iteratively, the observed variable means are always implicitly updated
with the robust weights. Therefore, in a sense all robust methods intrinsically analyze the mean structures of models. If
you do not specify the MEANSTR
option or any mean parameters for your models, PROC CALIS assumes appropriate saturated mean structures for the models. However,
when you are computing fit statistics, these saturated mean structures are ignored as if they were never modeled. If you do
specify the MEANSTR
option or any mean parameters for your models, these mean structures are taken into account in computing fit statistics.
In this release, robust estimation with the IRLS method is not supported when you specify the BOUNDS
, LINCON
, or NLINCON
statement. However, you can still set parameter constraints by using the same parameter names or by specifying the PARAMETERS
statement and the SAS programming statements
. See the section Setting Constraints on Parameters for techniques to set up implicit parameter constraints by using the PARAMETERS statement and SAS programming statements.
-
SALPHA=r
-
is an alias for the INSTEP=
option for line-search algorithms.
-
SBNTW=name
SBNTWGT=name
-
specifies the covariance matrix on which the normal-theory weight matrix is based when you use the Satorra-Bentler sandwich
formula to compute standard errors. You can specify the following names:
- OBS | OBSERVED
-
specifies that the observed covariance matrix be used.
- PRED | PREDICTED
-
specifies that the model-predicted covariance matrix be used.
By default, SBNTW=PRED. The SBNTW= option is applicable only when you specify the SE=SBSW
option or when you use METHOD=MLSB
. For more information, see the section Satorra-Bentler Sandwich Formula for Standard Errors.
-
SIMPLE
S
-
displays means, standard deviations,
skewness, and univariate kurtosis if available. This information is displayed when you specify the PRINT
option. If the KURTOSIS
option is specified, the SIMPLE option is set by default.
-
SINGULAR=r
SING=r
-
specifies the singularity
criterion r (0 < r < 1) used, for example, for matrix inversion. The default value is the square root of the relative machine precision or,
equivalently, the square root of the largest double precision value that, when added to 1, results in 1.
-
SLMW=r
-
specifies the probability limit used for computing
the stepwise multivariate Wald test. The process stops when the univariate probability is smaller than r. The default value is r=0.05.
-
SPRECISION=r
SP=r
-
is an alias for the LSPRECISION=
option.
-
START=r
-
specifies initial estimates for parameters as multiples of the r value.
In all CALIS models, you can supply initial estimates individually as parenthesized values after each parameter name. Unspecified
initial estimates are usually computed by various reasonable initial estimation methods in PROC CALIS. If none of the initialization
methods is able to compute all the unspecified initial estimates, then the remaining unspecified initial estimates are set
to r, 10 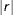 , or 100
, or 100 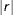 . For variance parameters, 100
. For variance parameters, 100 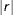 is used for covariance structure analyses and 10
is used for covariance structure analyses and 10 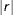 is used for correlation structure analyses. For other types of parameters, r is used. The default value is r = 0.5. If the DEMPHAS=
option is used, the initial values of the variance parameters are multiplied by the value specified in the DEMPHAS=
option. See the section Initial Estimates for more information.
is used for correlation structure analyses. For other types of parameters, r is used. The default value is r = 0.5. If the DEMPHAS=
option is used, the initial values of the variance parameters are multiplied by the value specified in the DEMPHAS=
option. See the section Initial Estimates for more information.
-
STDERR <=SBSW | UNADJ>
SE <=SBSW | UNADJ>
-
displays standard
error estimates if you use estimation methods other than unweighted least squares (ULS) or diagonally weighted least squares
(DWLS) and you do not specify the NOSTDERR
option. In contrast, the NOSTDERR
option suppresses the printing of the standard error estimates. If you specify neither the STDERR nor NOSTDERR option, the
standard errors are computed for the OUTMODEL=
data set. This information is displayed by default when you specify the PRINT
option.
Optionally, you can specify the method for computing standard errors. For METHOD=ML or GLS, the default is STDERR=UNADJ, where
the standard errors are computed by inverting an (unadjusted) approximate Hessian or information matrix. For METHOD=MLSB,
the default is STDERR=SBSW, where the sandwich formula proposed by Satorra and Bentler (1994) is used to adjust the computation of standard error estimates. Thus, the STDERR= option enables you to overwrite the default
standard error method for ML, MLSB, or GLS estimation. For METHOD=FIML or WLS, STDERR=UNADJ is assumed and cannot be overwritten.
You can specify the STDERR option in both the PROC CALIS and MODEL
statements. When you use this option in the MODEL statement, you can enable the standard error computation, but you cannot
specify the standard error method. The latter is possible only in the PROC CALIS statement. If you specify both the STDERR
and NOSTDERR options in the same statement, the STDERR option is ignored.
-
TMISSPAT | THRESHOLDMISSPAT | THRESMISSPAT=n
THRESHOLDMISSPAT=n
THRESMISSPAT=n
-
specifies the proportion threshold for the missing patterns to display in the
output, where n is between 0 and 1. The default TMISSPAT= value is 0.05. This option is relevant only when there are incomplete observations
(with some missing values in the analysis variables) in the input raw data set and when you use METHOD=
FIML or METHOD=
LSFIML for estimation.
Because the number of missing patterns could be quite large, PROC CALIS displays a limited number of the most frequent missing
patterns in the output. Together with the MAXMISSPAT=
option, this option controls the number of missing patterns to display in the output. See the MAXMISSPAT=
option for a detailed description about how the number of missing patterns to display is determined.
-
UPDATE=name
UPD=name
-
specifies the update method for the quasi-Newton or
conjugate-gradient optimization technique.
For OMETHOD=
CONGRA, the following updates
can be used:
- PB
-
performs the automatic restart update method of Powell (1977) and Beale (1972). This is the default.
- FR
-
performs the Fletcher-Reeves update (Fletcher 1980, p. 63).
- PR
-
performs the Polak-Ribiere update (Fletcher 1980, p. 66).
- CD
-
performs a conjugate-descent update of Fletcher (1987).
For OMETHOD=
DBLDOG, the following
updates (Fletcher 1987) can be used:
- DBFGS
-
performs the dual Broyden, Fletcher, Goldfarb, and Shanno (BFGS) update of the Cholesky factor of the Hessian matrix. This
is the default.
- DDFP
-
performs the dual Davidon, Fletcher, and Powell (DFP) update of the Cholesky factor of the Hessian matrix.
For OMETHOD=
QUANEW, the following updates (Fletcher 1987)
can be used:
- BFGS
-
performs original BFGS update of the inverse Hessian matrix. This is the default for earlier releases.
- DFP
-
performs the original DFP update of the inverse Hessian matrix.
- DBFGS
-
performs the dual BFGS update of the Cholesky factor of the Hessian matrix. This is the default.
- DDFP
-
performs the dual DFP update of the Cholesky factor of the Hessian matrix.
-
VARDEF= DF | N | WDF | WEIGHT | WGT
-
specifies the divisor used in the calculation
of covariances and standard deviations. The default value is VARDEF=N for the METHOD=FIML, and VARDEF=DF for other estimation
methods. The values and associated divisors are displayed in the following table, where k is the number of partial variables specified in the PARTIAL
statement. When a WEIGHT
statement is used, 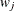 is the value of the WEIGHT variable in the jth observation, and the summation is performed only over observations with positive weight.
is the value of the WEIGHT variable in the jth observation, and the summation is performed only over observations with positive weight.
|
Value
|
Description
|
Divisor
|
|
DF
|
Degrees of freedom
|
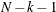
|
|
N
|
Number of observations
|
N
|
|
WDF
|
Sum of weights DF
|
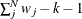
|
|
WEIGHT | WGT
|
Sum of weights
|
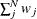
|
-
VSINGULAR=r
VSING=r
-
specifies a relative singularity
criterion r (r > 0) for the inversion of the information matrix, which is needed to compute the covariance matrix. If you do not specify
the SINGULAR=
option, the default value for r or VSING= is 1E–8; otherwise, the default value is SING, which is the specified SINGULAR=
value.
When inverting the information matrix, the following singularity criterion is used for the diagonal pivot 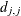 of the matrix:
of the matrix:
where ASING and MSING are the specified values of the ASINGULAR=
and MSINGULAR=
options, respectively, and 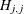 is the jth diagonal element of the information matrix. Note that in many cases a normalized matrix
is the jth diagonal element of the information matrix. Note that in many cases a normalized matrix 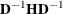 is decomposed (where
is decomposed (where 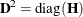 ), and the singularity criteria are modified correspondingly.
), and the singularity criteria are modified correspondingly.
-
WPENALTY=r
WPEN=r
-
specifies the penalty weight
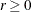 for the WLS and DWLS fit of the diagonal elements of a correlation matrix (constant 1s). The criterion for weighted least
squares estimation of a correlation structure is
for the WLS and DWLS fit of the diagonal elements of a correlation matrix (constant 1s). The criterion for weighted least
squares estimation of a correlation structure is
where r is the penalty weight specified by the WPENALTY=r option and the 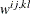 are the elements of the inverse of the reduced
are the elements of the inverse of the reduced 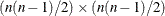 weight matrix that contains only the nonzero rows and columns of the full weight matrix
weight matrix that contains only the nonzero rows and columns of the full weight matrix 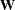 . The second term is a penalty term to fit the diagonal elements of the correlation matrix. The default value is 100. The
reciprocal of this value replaces the asymptotic variance corresponding to the diagonal elements of a correlation matrix in
the weight matrix
. The second term is a penalty term to fit the diagonal elements of the correlation matrix. The default value is 100. The
reciprocal of this value replaces the asymptotic variance corresponding to the diagonal elements of a correlation matrix in
the weight matrix 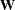 , and it is effective only with the ASYCOV=
CORR option, which is the default for correlation analyses. The often used value r = 1 seems to be too small in many cases to fit the diagonal elements of a correlation matrix properly. The default WPENALTY=
value emphasizes the importance of the fit of the diagonal elements in the correlation matrix. You can decrease or increase
the value of r if you want to decrease or increase the importance of the diagonal elements fit. This option is effective only with the WLS
or DWLS estimation method and the analysis of a correlation matrix.
, and it is effective only with the ASYCOV=
CORR option, which is the default for correlation analyses. The often used value r = 1 seems to be too small in many cases to fit the diagonal elements of a correlation matrix properly. The default WPENALTY=
value emphasizes the importance of the fit of the diagonal elements in the correlation matrix. You can decrease or increase
the value of r if you want to decrease or increase the importance of the diagonal elements fit. This option is effective only with the WLS
or DWLS estimation method and the analysis of a correlation matrix.
See the section Estimation Criteria for more details.
Caution: If you input the weight matrix by the INWGT=
option, the WPENALTY= option is ignored.
-
WRIDGE=r
-
defines a ridge factor r for the
diagonal of the weight matrix 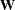 used in GLS, WLS, or DWLS estimation. The weight matrix
used in GLS, WLS, or DWLS estimation. The weight matrix 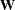 is transformed to
is transformed to
The WRIDGE= option is applied on the weight matrix before the following actions occur:
-
the WPENALTY=
option is applied on it
-
the weight matrix is written to the OUTWGT=
data set
-
the weight matrix is displayed
Caution: If you input the weight matrix by the INWGT=
option, the OUTWGT=
data set will contain the same weight matrix without the ridging requested by the WRIDGE= option. This ensures that the entries
in the INWGT=
and OUTWGT=
data sets are consistent. The WRIDGE= option is ignored if you input the inverse of the weight matrix by the INWGT=
and INWGTINV
options (or the INWGT(INV)=
option alone).
-
XCONV=r
XTOL=r
-
specifies the relative parameter convergence criterion.
Termination requires a small relative parameter (x) change in subsequent iterations, that is,
The default value for r is 1E–8 for robust estimation (see the ROBUST
option) with the iteratively reweighted least squares method, and it is 0 for other estimation methods. The default value
for XSIZE is 0. You can change this default value by specifying the XSIZE= option in the NLOPTIONS
statement.


 Classes of Statements in PROC CALISSingle-Group Analysis SyntaxMultiple-Group Multiple-Model Analysis SyntaxPROC CALIS StatementBOUNDS StatementBY StatementCOSAN StatementCOV StatementDETERM StatementEFFPART StatementFACTOR StatementFITINDEX StatementFREQ StatementGROUP StatementLINCON StatementLINEQS StatementLISMOD StatementLMTESTS StatementMATRIX StatementMEAN StatementMODEL StatementMSTRUCT StatementNLINCON StatementNLOPTIONS StatementOUTFILES StatementPARAMETERS StatementPARTIAL StatementPATH StatementPATHDIAGRAM StatementPCOV StatementPVAR StatementRAM StatementREFMODEL StatementRENAMEPARM StatementSAS Programming StatementsSIMTESTS StatementSTD StatementSTRUCTEQ StatementTESTFUNC StatementVAR StatementVARIANCE StatementVARNAMES StatementWEIGHT Statement
Classes of Statements in PROC CALISSingle-Group Analysis SyntaxMultiple-Group Multiple-Model Analysis SyntaxPROC CALIS StatementBOUNDS StatementBY StatementCOSAN StatementCOV StatementDETERM StatementEFFPART StatementFACTOR StatementFITINDEX StatementFREQ StatementGROUP StatementLINCON StatementLINEQS StatementLISMOD StatementLMTESTS StatementMATRIX StatementMEAN StatementMODEL StatementMSTRUCT StatementNLINCON StatementNLOPTIONS StatementOUTFILES StatementPARAMETERS StatementPARTIAL StatementPATH StatementPATHDIAGRAM StatementPCOV StatementPVAR StatementRAM StatementREFMODEL StatementRENAMEPARM StatementSAS Programming StatementsSIMTESTS StatementSTD StatementSTRUCTEQ StatementTESTFUNC StatementVAR StatementVARIANCE StatementVARNAMES StatementWEIGHT Statement Input Data SetsOutput Data SetsDefault Analysis Type and Default ParameterizationThe COSAN ModelThe FACTOR ModelThe LINEQS ModelThe LISMOD Model and SubmodelsThe MSTRUCT ModelThe PATH ModelThe RAM ModelNaming Variables and ParametersSetting Constraints on ParametersAutomatic Variable SelectionPath Diagrams: Layout Algorithms, Default Settings, and CustomizationEstimation CriteriaRelationships among Estimation CriteriaGradient, Hessian, Information Matrix, and Approximate Standard ErrorsCounting the Degrees of FreedomAssessment of FitCase-Level Residuals, Outliers, Leverage Observations, and Residual DiagnosticsLatent Variable ScoresTotal, Direct, and Indirect EffectsStandardized SolutionsModification IndicesMissing Values and the Analysis of Missing PatternsMeasures of Multivariate KurtosisInitial EstimatesUse of Optimization TechniquesComputational ProblemsDisplayed OutputODS Table NamesODS Graphics
Input Data SetsOutput Data SetsDefault Analysis Type and Default ParameterizationThe COSAN ModelThe FACTOR ModelThe LINEQS ModelThe LISMOD Model and SubmodelsThe MSTRUCT ModelThe PATH ModelThe RAM ModelNaming Variables and ParametersSetting Constraints on ParametersAutomatic Variable SelectionPath Diagrams: Layout Algorithms, Default Settings, and CustomizationEstimation CriteriaRelationships among Estimation CriteriaGradient, Hessian, Information Matrix, and Approximate Standard ErrorsCounting the Degrees of FreedomAssessment of FitCase-Level Residuals, Outliers, Leverage Observations, and Residual DiagnosticsLatent Variable ScoresTotal, Direct, and Indirect EffectsStandardized SolutionsModification IndicesMissing Values and the Analysis of Missing PatternsMeasures of Multivariate KurtosisInitial EstimatesUse of Optimization TechniquesComputational ProblemsDisplayed OutputODS Table NamesODS Graphics Estimating Covariances and CorrelationsEstimating Covariances and Means SimultaneouslyTesting Uncorrelatedness of VariablesTesting Covariance PatternsTesting Some Standard Covariance Pattern HypothesesLinear Regression ModelMultivariate Regression ModelsMeasurement Error ModelsTesting Specific Measurement Error ModelsMeasurement Error Models with Multiple PredictorsMeasurement Error Models Specified As Linear EquationsConfirmatory Factor ModelsConfirmatory Factor Models: Some VariationsResidual Diagnostics and Robust EstimationThe Full Information Maximum Likelihood MethodComparing the ML and FIML EstimationPath Analysis: Stability of AlienationSimultaneous Equations with Mean Structures and Reciprocal PathsFitting Direct Covariance StructuresConfirmatory Factor Analysis: Cognitive AbilitiesTesting Equality of Two Covariance Matrices Using a Multiple-Group AnalysisTesting Equality of Covariance and Mean Matrices between Independent GroupsIllustrating Various General Modeling LanguagesTesting Competing Path Models for the Career Aspiration DataFitting a Latent Growth Curve ModelHigher-Order and Hierarchical Factor ModelsLinear Relations among Factor LoadingsMultiple-Group Model for Purchasing BehaviorFitting the RAM and EQS Models by the COSAN Modeling LanguageSecond-Order Confirmatory Factor AnalysisLinear Relations among Factor Loadings: COSAN Model SpecificationOrdinal Relations among Factor LoadingsLongitudinal Factor Analysis
Estimating Covariances and CorrelationsEstimating Covariances and Means SimultaneouslyTesting Uncorrelatedness of VariablesTesting Covariance PatternsTesting Some Standard Covariance Pattern HypothesesLinear Regression ModelMultivariate Regression ModelsMeasurement Error ModelsTesting Specific Measurement Error ModelsMeasurement Error Models with Multiple PredictorsMeasurement Error Models Specified As Linear EquationsConfirmatory Factor ModelsConfirmatory Factor Models: Some VariationsResidual Diagnostics and Robust EstimationThe Full Information Maximum Likelihood MethodComparing the ML and FIML EstimationPath Analysis: Stability of AlienationSimultaneous Equations with Mean Structures and Reciprocal PathsFitting Direct Covariance StructuresConfirmatory Factor Analysis: Cognitive AbilitiesTesting Equality of Two Covariance Matrices Using a Multiple-Group AnalysisTesting Equality of Covariance and Mean Matrices between Independent GroupsIllustrating Various General Modeling LanguagesTesting Competing Path Models for the Career Aspiration DataFitting a Latent Growth Curve ModelHigher-Order and Hierarchical Factor ModelsLinear Relations among Factor LoadingsMultiple-Group Model for Purchasing BehaviorFitting the RAM and EQS Models by the COSAN Modeling LanguageSecond-Order Confirmatory Factor AnalysisLinear Relations among Factor Loadings: COSAN Model SpecificationOrdinal Relations among Factor LoadingsLongitudinal Factor Analysis
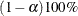
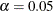
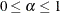
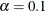
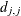
![\[ |d_{j,j}| \le \max (\emph{ASING}, \emph{VSING} * |H_{j,j}|, \emph{MSING} * \max (|H_{1,1}|,\ldots ,|H_{n,n}|)) \]](images/statug_calis0016.png)
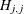
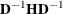
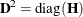
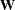

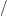
![\[ \chi ^2 = (1 - \mi{c})(\mi{N} - \mi{k})\mi{F} \]](images/statug_calis0023.png)
![\[ \mi{c} = \frac{\mi{p}(\mi{p} + 1)^2(2 \mi{p} - 3)}{6 \mi{n}(\mi{p} - 1)(\mi{p}^2 + \mi{p} - 4)} \]](images/statug_calis0024.png)
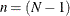
![\[ \mi{c} = \frac{2 \mi{p}^2 + 3 \mi{p} - 1}{6 (\mi{p} + 1) (\mi{k} - 1)} ( \sum _{i=1}^ k \frac{1}{\mi{n}_ i} - \frac{1}{\sum _{i=1}^ k \mi{n}_ i}) \]](images/statug_calis0026.png)
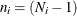
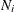
![\[ \mi{c} = \frac{1}{6 \mi{n}}(2 \mi{p} + 1 - \frac{2}{\mi{p} + 1}) \]](images/statug_calis0029.png)
![\[ \mi{c} = \frac{2 \mi{p}^2 + \mi{p} + 2}{6 \mi{n}\mi{p}} \]](images/statug_calis0030.png)
![\[ \mi{c} = \frac{2 \mi{p}^2 - 3 \mi{p} + 3}{6 \mi{n}(\mi{p}-1)} \]](images/statug_calis0031.png)
![\[ \mi{c} = \frac{2 \mi{p} + 5}{6 \mi{n}} \]](images/statug_calis0032.png)
![\[ \bSigma = \left( \begin{array}{cccc} v & c & c & c \\ c & v & c & c \\ c & c & v & c \\ c & c & c & v \\ \end{array} \right) \quad \]](images/statug_calis0033.png)
![\[ H_0 : \bSigma _1 = \bSigma _2 = \ldots = \bSigma _ k = \bSigma \]](images/statug_calis0034.png)
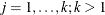
![\[ H_0 : \bSigma = \sigma ^2 \mb{I} \]](images/statug_calis0038.png)
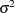
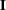
![\[ \bSigma = \left( \begin{array}{ccc} v & 0 & 0 \\ 0 & v & 0 \\ 0 & 0 & v \\ \end{array} \right) \quad \]](images/statug_calis0041.png)
![\[ \bSigma = \left( \begin{array}{ccc} v_1 & 0 & 0 \\ 0 & v_2 & 0 \\ 0 & 0 & v_3 \\ \end{array} \right) \quad \]](images/statug_calis0042.png)
![\[ s_{\mathit{new}} = r (|s_\mathit {{old}}| + 1) \]](images/statug_calis0046.png)
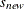
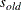
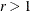
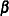
![\[ \frac{ |f(x^{(k)}) - f(x^{(k-1)})| }{ \max (|f(x^{(k-1)})|,\emph{FSIZE}) } \leq r \]](images/statug_calis0052.png)
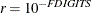
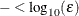

![\[ \frac{ [g(x^{(k)})]^{\prime } [\mb{G}^{(k)}]^{-1} g(x^{(k)}) }{\max (|f(x^{(k)})|,\emph{FSIZE}) } \leq r \]](images/statug_calis0056.png)
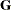
![\[ \frac{ \parallel g(x^{(k)}) \parallel _2^2 \quad \parallel s(x^{(k)}) \parallel _2}{ \parallel g(x^{(k)}) - g(x^{(k-1)}) \parallel _2 \max (|f(x^{(k)})|,\emph{FSIZE}) } \leq r \]](images/statug_calis0058.png)
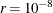
![\[ H_0 : \bmu _1 = \bmu _2 = \ldots = \bmu _ k = \bmu \]](images/statug_calis0060.png)
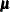
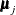
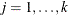
![\[ \bmu = \left( \begin{array}{c} m_1 \\ m_2 \\ m_3 \\ m_4 \\ \end{array} \right) \quad \]](images/statug_calis0064.png)
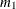
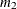
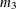
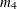
![\[ \bmu = \left( \begin{array}{c} m_1 \\ m_2 \\ m_3 \\ \end{array} \right) \quad \]](images/statug_calis0069.png)
![\[ \bmu = \left( \begin{array}{c} m \\ m \\ m \\ \end{array} \right) \quad \]](images/statug_calis0070.png)
![\[ \bmu = \left( \begin{array}{c} 0 \\ 0 \\ 0 \\ 0 \\ \end{array} \right) \quad \]](images/statug_calis0071.png)
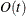
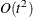
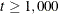
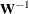
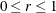
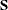
![\[ \mb{S} \longrightarrow \tilde{\mb{S}} = \mb{S} + r (\mr{diag}(\mb{S})) \]](images/statug_calis0080.png)
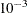
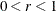
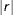
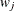
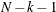
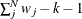
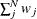
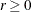
![\[ \mb{F}_{\mathit{WLS}} = {\sum _{i=2}^ n \sum _{j=1}^{i-1} \sum _{k=2}^ n \sum _{l=1}^{k-1} w^{ij,kl} (s_{ij} - c_{ij})(s_{kl} - c_{kl}) } + r \sum _ i^ n (s_{ii} - c_{ii})^2 \]](images/statug_calis0091.png)
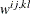
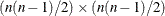
![\[ \mb{W} \longrightarrow \tilde{\mb{W}} = \mb{W} + r (\mr{diag}(\mb{W})) \]](images/statug_calis0094.png)
![\[ \frac{\max _ j |x_ j^{(k)} - x_ j^{(k-1)}|}{\max (|x_ j^{(k)}|,|x_ j^{(k-1)}|,\Argument{XSIZE})} \leq r \]](images/statug_calis0095.png)