The CALIS Procedure
-
Overview

-
Getting Started

-
Syntax
 Classes of Statements in PROC CALISSingle-Group Analysis SyntaxMultiple-Group Multiple-Model Analysis SyntaxPROC CALIS StatementBOUNDS StatementBY StatementCOSAN StatementCOV StatementDETERM StatementEFFPART StatementFACTOR StatementFITINDEX StatementFREQ StatementGROUP StatementLINCON StatementLINEQS StatementLISMOD StatementLMTESTS StatementMATRIX StatementMEAN StatementMODEL StatementMSTRUCT StatementNLINCON StatementNLOPTIONS StatementOUTFILES StatementPARAMETERS StatementPARTIAL StatementPATH StatementPATHDIAGRAM StatementPCOV StatementPVAR StatementRAM StatementREFMODEL StatementRENAMEPARM StatementSAS Programming StatementsSIMTESTS StatementSTD StatementSTRUCTEQ StatementTESTFUNC StatementVAR StatementVARIANCE StatementVARNAMES StatementWEIGHT Statement
Classes of Statements in PROC CALISSingle-Group Analysis SyntaxMultiple-Group Multiple-Model Analysis SyntaxPROC CALIS StatementBOUNDS StatementBY StatementCOSAN StatementCOV StatementDETERM StatementEFFPART StatementFACTOR StatementFITINDEX StatementFREQ StatementGROUP StatementLINCON StatementLINEQS StatementLISMOD StatementLMTESTS StatementMATRIX StatementMEAN StatementMODEL StatementMSTRUCT StatementNLINCON StatementNLOPTIONS StatementOUTFILES StatementPARAMETERS StatementPARTIAL StatementPATH StatementPATHDIAGRAM StatementPCOV StatementPVAR StatementRAM StatementREFMODEL StatementRENAMEPARM StatementSAS Programming StatementsSIMTESTS StatementSTD StatementSTRUCTEQ StatementTESTFUNC StatementVAR StatementVARIANCE StatementVARNAMES StatementWEIGHT Statement -
Details
 Input Data SetsOutput Data SetsDefault Analysis Type and Default ParameterizationThe COSAN ModelThe FACTOR ModelThe LINEQS ModelThe LISMOD Model and SubmodelsThe MSTRUCT ModelThe PATH ModelThe RAM ModelNaming Variables and ParametersSetting Constraints on ParametersAutomatic Variable SelectionPath Diagrams: Layout Algorithms, Default Settings, and CustomizationEstimation CriteriaRelationships among Estimation CriteriaGradient, Hessian, Information Matrix, and Approximate Standard ErrorsCounting the Degrees of FreedomAssessment of FitCase-Level Residuals, Outliers, Leverage Observations, and Residual DiagnosticsLatent Variable ScoresTotal, Direct, and Indirect EffectsStandardized SolutionsModification IndicesMissing Values and the Analysis of Missing PatternsMeasures of Multivariate KurtosisInitial EstimatesUse of Optimization TechniquesComputational ProblemsDisplayed OutputODS Table NamesODS Graphics
Input Data SetsOutput Data SetsDefault Analysis Type and Default ParameterizationThe COSAN ModelThe FACTOR ModelThe LINEQS ModelThe LISMOD Model and SubmodelsThe MSTRUCT ModelThe PATH ModelThe RAM ModelNaming Variables and ParametersSetting Constraints on ParametersAutomatic Variable SelectionPath Diagrams: Layout Algorithms, Default Settings, and CustomizationEstimation CriteriaRelationships among Estimation CriteriaGradient, Hessian, Information Matrix, and Approximate Standard ErrorsCounting the Degrees of FreedomAssessment of FitCase-Level Residuals, Outliers, Leverage Observations, and Residual DiagnosticsLatent Variable ScoresTotal, Direct, and Indirect EffectsStandardized SolutionsModification IndicesMissing Values and the Analysis of Missing PatternsMeasures of Multivariate KurtosisInitial EstimatesUse of Optimization TechniquesComputational ProblemsDisplayed OutputODS Table NamesODS Graphics -
Examples
 Estimating Covariances and CorrelationsEstimating Covariances and Means SimultaneouslyTesting Uncorrelatedness of VariablesTesting Covariance PatternsTesting Some Standard Covariance Pattern HypothesesLinear Regression ModelMultivariate Regression ModelsMeasurement Error ModelsTesting Specific Measurement Error ModelsMeasurement Error Models with Multiple PredictorsMeasurement Error Models Specified As Linear EquationsConfirmatory Factor ModelsConfirmatory Factor Models: Some VariationsResidual Diagnostics and Robust EstimationThe Full Information Maximum Likelihood MethodComparing the ML and FIML EstimationPath Analysis: Stability of AlienationSimultaneous Equations with Mean Structures and Reciprocal PathsFitting Direct Covariance StructuresConfirmatory Factor Analysis: Cognitive AbilitiesTesting Equality of Two Covariance Matrices Using a Multiple-Group AnalysisTesting Equality of Covariance and Mean Matrices between Independent GroupsIllustrating Various General Modeling LanguagesTesting Competing Path Models for the Career Aspiration DataFitting a Latent Growth Curve ModelHigher-Order and Hierarchical Factor ModelsLinear Relations among Factor LoadingsMultiple-Group Model for Purchasing BehaviorFitting the RAM and EQS Models by the COSAN Modeling LanguageSecond-Order Confirmatory Factor AnalysisLinear Relations among Factor Loadings: COSAN Model SpecificationOrdinal Relations among Factor LoadingsLongitudinal Factor Analysis
Estimating Covariances and CorrelationsEstimating Covariances and Means SimultaneouslyTesting Uncorrelatedness of VariablesTesting Covariance PatternsTesting Some Standard Covariance Pattern HypothesesLinear Regression ModelMultivariate Regression ModelsMeasurement Error ModelsTesting Specific Measurement Error ModelsMeasurement Error Models with Multiple PredictorsMeasurement Error Models Specified As Linear EquationsConfirmatory Factor ModelsConfirmatory Factor Models: Some VariationsResidual Diagnostics and Robust EstimationThe Full Information Maximum Likelihood MethodComparing the ML and FIML EstimationPath Analysis: Stability of AlienationSimultaneous Equations with Mean Structures and Reciprocal PathsFitting Direct Covariance StructuresConfirmatory Factor Analysis: Cognitive AbilitiesTesting Equality of Two Covariance Matrices Using a Multiple-Group AnalysisTesting Equality of Covariance and Mean Matrices between Independent GroupsIllustrating Various General Modeling LanguagesTesting Competing Path Models for the Career Aspiration DataFitting a Latent Growth Curve ModelHigher-Order and Hierarchical Factor ModelsLinear Relations among Factor LoadingsMultiple-Group Model for Purchasing BehaviorFitting the RAM and EQS Models by the COSAN Modeling LanguageSecond-Order Confirmatory Factor AnalysisLinear Relations among Factor Loadings: COSAN Model SpecificationOrdinal Relations among Factor LoadingsLongitudinal Factor Analysis - References
Example 29.26 Higher-Order and Hierarchical Factor Models
In this example, confirmatory higher-order and hierarchical factor models are fitted by PROC CALIS.
In higher-order factor models, factors are at different levels. The higher-order factors explain the relationships among factors
at the next lower level, in the same way that the first-order factors explain the relationships among manifest variables.
For example, in a two-level higher order factor model you have nine manifest variables V1–V9 with three first-order factors F1–F3. The first-order factor pattern of the model might appear like the following:
F1 F2 F3
V1 x
V2 x
V3 x
V4 x
V5 x
V6 x
V7 x
V8 x
V9 x
where each "x" marks a nonzero factor loading and all other unmarked entries are fixed zeros in the model. To explain the
correlations among the first-order factors, a second-order factor F4 is hypothesized with the following second-order factor pattern:
F4
F1 x
F2 x
F3 x
If substantiated by your theory, you might have higher-order factor models with more than two levels.
In hierarchical factor models, all factors are at the same (first-order) level but are different in their clusters of manifest variables related. Using the terminology of Yung, Thissen, and McLeod (1999), factors in hierarchical factor models are classified into "layers." The factors in the first layer partition the manifest variables into clusters so that each factor has a distinct cluster of related manifest variables. This part of the factor pattern of the hierarchical factor model is similar to that of the first-order factor model for manifest variables. The next layer of factors in the hierarchical factor model again partitions the manifest variables into clusters. However, this time each cluster contains at least two clusters of manifest variables that are formed in the previous layer. For example, the following is a factor pattern of a confirmatory hierarchical factor model with two layers:
First Layer | Second Layer
F1 F2 F3 | F4
V1 x | x
V2 x | x
V3 x | x
V4 x | x
V5 x | x
V6 x | x
V7 x | x
V8 x | x
V9 x | x
F1–F3 are first-layer factors and F4 is the only second-layer factor. This special kind of two-layer hierarchical pattern is also known as the bifactor solution.
In a bifactor solution, there are two classes of factors—group factors and a general factor. For example, in the preceding
hierarchical factor pattern F1–F3 are group factors for different abilities and F4 is a general factor such as "intelligence" (see, for example, Holzinger and Swineford 1937). See Mulaik and Quartetti (1997) for more examples and distinctions among various types of hierarchical factor models. Certainly, if substantiated by your
theory, hierarchical factor models with more than two layers are possible.
In this example, you use PROC CALIS to fit these two types of confirmatory factor models. First, you fit a second-order factor model to a real data set. Then you fit a bifactor model to the same data set. In the final section of this example, an informal account of the relationship between the higher-order and hierarchical factor models is attempted. Techniques for constraining parameters using PROC CALIS are also shown. This final section might be too technical in the first reading. Interested readers are referred to articles by Mulaik and Quartetti (1997), Schmid and Leiman (1957), and Yung, Thissen, and McLeod (1999) for more details.
A Second-Order Factor Analysis Model
In this section, a second-order confirmatory factor analysis model is applied to a correlation matrix of Thurstone reported by McDonald (1985). The correlation matrix is read into a SAS data set in the following statements:
data Thurst(type=corr);
title "Example of THURSTONE resp. McDONALD (1985, p.57, p.105)";
_type_ = 'corr'; input _name_ $ V1-V9;
label V1='Sentences' V2='Vocabulary' V3='Sentence Completion'
V4='First Letters' V5='Four-letter Words' V6='Suffices'
V7='Letter series' V8='Pedigrees' V9='Letter Grouping';
datalines;
V1 1. . . . . . . . .
V2 .828 1. . . . . . . .
V3 .776 .779 1. . . . . . .
V4 .439 .493 .460 1. . . . . .
V5 .432 .464 .425 .674 1. . . . .
V6 .447 .489 .443 .590 .541 1. . . .
V7 .447 .432 .401 .381 .402 .288 1. . .
V8 .541 .537 .534 .350 .367 .320 .555 1. .
V9 .380 .358 .359 .424 .446 .325 .598 .452 1.
;
Variables in this data set are measures of cognitive abilities. Three factors are assumed for these nine variable V1–V9. These three factors are the first-order factors in the analysis. A second-order factor is also assumed to explain the correlations
among the three first-order factors.
The following statements define a second-order factor model by using the LINEQS modeling language.
proc calis corr data=Thurst method=max nobs=213 nose nostand;
lineqs
V1 = X11 * Factor1 + E1,
V2 = X21 * Factor1 + E2,
V3 = X31 * Factor1 + E3,
V4 = X42 * Factor2 + E4,
V5 = X52 * Factor2 + E5,
V6 = X62 * Factor2 + E6,
V7 = X73 * Factor3 + E7,
V8 = X83 * Factor3 + E8,
V9 = X93 * Factor3 + E9,
Factor1 = L1g * FactorG + E10,
Factor2 = L2g * FactorG + E11,
Factor3 = L3g * FactorG + E12;
variance
FactorG = 1. ,
E1-E12 = U1-U9 W1-W3;
bounds
0. <= U1-U9;
fitindex ON(ONLY)=[chisq df probchi];
/* SAS Programming Statements: Dependent parameter definitions */
W1 = 1. - L1g * L1g;
W2 = 1. - L2g * L2g;
W3 = 1. - L3g * L3g;
run;
In the first nine equations of the LINEQS
statement, variables V1–V3 are manifest indicators of latent factor Factor1, variables V4–V6 are manifest indicators of latent factor Factor2, and variables V7–V9 are manifest indicators of latent factor Factor3. In the last three equations of the LINEQS
statement, the three first-order factors Factor1–Factor3 are explained by a common source: FactorG. Hence, Factor1–Factor3 are correlated due to the common source FactorG in the model.
An error term is added to each equation in the LINEQS statement. These error terms E1–E12 are needed because the factors are not assumed to be perfect predictors of the corresponding outcome variables.
In the VARIANCE
statement, you specify variance parameters for all independent or exogenous variables in the model: FactorG, and E1–E12. The variance of FactorG is fixed at one for identification. Variances for E1–E9 are given parameter names U1–U9, respectively. Variances for E10–E12 are given parameter names W1–W3, respectively. Note that for model identification purposes, W1–W3 are defined as dependent parameters in the SAS programming statements
. That is,
![\[ W_ i = 1. - L_{ig}^2 \quad (i=1,2,3) \]](images/statug_calis1012.png)
These dependent parameter definitions ensure that the variances for Factor1–Factor3 are fixed at ones for identification.
In the BOUNDS
statement, you specify that variance parameters U1–U9 must be positive in the solution.
In addition to the statements for model specification, you specify some output control options in the PROC CALIS statement. You use the NOSE and NOSTAND options suppress the display of standard errors and standardized results. In the FITINDEX statement, the ON(ONLY)= option requests only the model fit chi-square and its associated degrees of freedom and p-value be shown in the fit summary table. Using printing options in PROC CALIS to reduce the amount the of printout is a good practice. It makes your output more focused, as you output only what you need in a particular situation.
In Output 29.26.1, parameters and their initial values, gradients, and bounds are shown.
Output 29.26.1: Parameters in the Model
| Optimization Start Parameter Estimates |
|||||
|---|---|---|---|---|---|
| N | Parameter | Estimate | Gradient | Lower Bound | Upper Bound |
| 1 | X11 | 1.00000 | 0.13476 | . | . |
| 2 | X21 | 1.01408 | 0.17327 | . | . |
| 3 | X31 | 0.95518 | 0.12174 | . | . |
| 4 | X42 | 1.00000 | 0.22548 | . | . |
| 5 | X52 | 0.96603 | 0.21304 | . | . |
| 6 | X62 | 0.88305 | 0.19782 | . | . |
| 7 | X73 | 1.00000 | 0.21041 | . | . |
| 8 | X83 | 1.03403 | 0.39324 | . | . |
| 9 | X93 | 0.91752 | 0.19880 | . | . |
| 10 | L1g | 0.75060 | -0.57492 | . | . |
| 11 | L2g | 0.64268 | -0.50975 | . | . |
| 12 | L3g | 0.60919 | -0.56538 | . | . |
| 13 | U1 | 0.18879 | 0.14837 | 0 | . |
| 14 | U2 | 0.16579 | 0.08989 | 0 | . |
| 15 | U3 | 0.25988 | -0.03231 | 0 | . |
| 16 | U4 | 0.33068 | 0.20120 | 0 | . |
| 17 | U5 | 0.37538 | 0.09124 | 0 | . |
| 18 | U6 | 0.47808 | -0.03595 | 0 | . |
| 19 | U7 | 0.44813 | 0.20918 | 0 | . |
| 20 | U8 | 0.40994 | -0.12469 | 0 | . |
| 21 | U9 | 0.53541 | 0.05959 | 0 | . |
| Value of Objective Function = 0.5693888709 | |||||
The first table contains all the independent parameters. There are twenty-one in total. Parameters W1–W3, which are defined in the SAS programming statements
, are shown in the next table for dependent parameters. Their initial values are computed as functions of the independent
parameters.
Output 29.26.2 shows the information about optimization—iteration history and the convergence status.
Output 29.26.2: Optimization
| Iteration | Restarts | Function Calls |
Active Constraints |
Objective Function |
Objective Function Change |
Max Abs Gradient Element |
Lambda | Ratio Between Actual and Predicted Change |
||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 5 | 0 | 0.38684 | 0.1825 | 0.5158 | 3.214 | 1.174 | ||
| 2 | 0 | 9 | 0 | 0.18706 | 0.1998 | 0.1003 | 0 | 1.181 | ||
| 3 | 0 | 11 | 0 | 0.18039 | 0.00667 | 0.0273 | 0 | 0.987 | ||
| 4 | 0 | 13 | 0 | 0.18020 | 0.000192 | 0.00581 | 0 | 0.881 | ||
| 5 | 0 | 15 | 0 | 0.18017 | 0.000023 | 0.00295 | 0 | 0.967 | ||
| 6 | 0 | 17 | 0 | 0.18017 | 3.08E-6 | 0.000686 | 0 | 1.083 | ||
| 7 | 0 | 19 | 0 | 0.18017 | 4.606E-7 | 0.000379 | 0 | 1.195 | ||
| 8 | 0 | 21 | 0 | 0.18017 | 7.365E-8 | 0.000096 | 0 | 1.283 | ||
| 9 | 0 | 23 | 0 | 0.18017 | 1.228E-8 | 0.000054 | 0 | 1.342 | ||
| 10 | 0 | 25 | 0 | 0.18017 | 2.098E-9 | 0.000018 | 0 | 1.377 | ||
| 11 | 0 | 27 | 0 | 0.18017 | 3.63E-10 | 8.561E-6 | 0 | 1.397 |
First, there are 21 independent parameters in the optimization by using 45 "Functions (Observations)." The so-called functions refer to the moments in the model that are structured with parameters. Nine lower bounds, which are specified for the error variance parameters, are specified in the optimization. The next table for iteration history shows that the optimization stops in 11 iterations. The notes at the bottom of table show that the solution converges without problems.
Output 29.26.3 shows the fit summary table. The chi-square model fit value is 38.196, with df = 24, and p = 0.033. This indicates a satisfactory model fit.
Output 29.26.4 shows the fitted equations with final estimates. Interpretations of these loadings are not done here. The last table in this output shows various variance estimates. These estimates are classified by whether they are for the latent variables, error variables, or disturbance variables.
Output 29.26.4: Estimation Results
| Linear Equations | |||||||
|---|---|---|---|---|---|---|---|
| V1 | = | 0.9047 | Factor1 | + | 1.0000 | E1 | |
| V2 | = | 0.9138 | Factor1 | + | 1.0000 | E2 | |
| V3 | = | 0.8561 | Factor1 | + | 1.0000 | E3 | |
| V4 | = | 0.8358 | Factor2 | + | 1.0000 | E4 | |
| V5 | = | 0.7972 | Factor2 | + | 1.0000 | E5 | |
| V6 | = | 0.7026 | Factor2 | + | 1.0000 | E6 | |
| V7 | = | 0.7808 | Factor3 | + | 1.0000 | E7 | |
| V8 | = | 0.7202 | Factor3 | + | 1.0000 | E8 | |
| V9 | = | 0.7035 | Factor3 | + | 1.0000 | E9 | |
| Factor1 | = | 0.8221 | FactorG | + | 1.0000 | E10 | |
| Factor2 | = | 0.7818 | FactorG | + | 1.0000 | E11 | |
| Factor3 | = | 0.8150 | FactorG | + | 1.0000 | E12 | |
For illustration purposes, you might check whether the model constraints put on the variances of Factor1–Factor3 are honored (although this should have been taken care of in the optimization). For example, the variance of Factor1 should be:
![\[ 1 = (\mbox{Loading on FactorG})^2 + \mbox{Variance of E10} \]](images/statug_calis1013.png)
Extracting the estimates from the output, you indeed verify the required equality, as shown in the following:
![\[ 1.0000 = (0.8221)^2 + 0.32420 \]](images/statug_calis1014.png)
A Bifactor Model
A bifactor model (or a hierarchical factor model with two layers) for the same data set is now considered. In this model,
the same set of factors as in the preceding higher-order factor model are used. The most notable difference is that the second-order
factor FactorG in the higher-order factor model is no longer a factor of the first-order factors Factor1–Factor3. Instead, FactorG, like Factor1–Factor3, now also serves as a factor of the observed variable V1–V9. Unlike Factor1–Factor3, FactorG is considered to be a general factor in the sense that all observed variables have direct functional relationships with it. In contrast, Factor1–Factor3 are group factors in the sense that each of them has a direct functional relationship with only one group of observed variables. Because of the coexistence of a general factor and group factors at the same factor level, such a hierarchical
model is also called a bifactor model.
The bifactor model is specified in the following statements:
proc calis corr data=Thurst method=max nobs=213 nose nostand;
lineqs
V1 = X11 * Factor1 + X1g * FactorG + E1,
V2 = X21 * Factor1 + X2g * FactorG + E2,
V3 = X31 * Factor1 + X3g * FactorG + E3,
V4 = X42 * Factor2 + X4g * FactorG + E4,
V5 = X52 * Factor2 + X5g * FactorG + E5,
V6 = X62 * Factor2 + X6g * FactorG + E6,
V7 = X73 * Factor3 + X7g * FactorG + E7,
V8 = X83 * Factor3 + X8g * FactorG + E8,
V9 = X93 * Factor3 + X9g * FactorG + E9;
variance
Factor1-Factor3 = 3 * 1.,
FactorG = 1. ,
E1-E9 = U1-U9;
cov
Factor1-Factor3 FactorG = 6 * 0.;
bounds
0. <= U1-U9;
fitindex ON(ONLY)=[chisq df probchi];
run;
In the LINEQS
statement, there are only nine equations for the manifest variables in the model. Unlike the second-order factor model fitted
previously, Factor1–Factor3 are no longer functionally related to FactorG and therefore there are no equations with Factor1–Factor3 as outcome variables.
The factor variances are all fixed at 1 in the VARIANCE
statement. The variance parameters for E1–E9 are named U1–U9, respectively. The BOUNDS
statement, again, is specified so that only positive estimates are accepted for error variance estimates.
All factors in the bifactor model are uncorrelated. In the COV
statement, you specify that the six covariances among Factor1–Factor3 and FactorG are all zero. This specification is necessary because by default exogenous variables (excluding error terms) in the LINEQS
model are correlated.
Like the previous PROC CALIS run, options are specified in the PROC CALIS and the FITINDEX statements to reduce the amount of default output.
There are more parameters in this model than in the preceding higher-order factor model, as shown in Output 29.26.5, which shows the optimization information.
Output 29.26.5: Optimization
| Iteration | Restarts | Function Calls |
Active Constraints |
Objective Function |
Objective Function Change |
Max Abs Gradient Element |
Lambda | Ratio Between Actual and Predicted Change |
||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 5 | 0 | 0.70566 | 0.1324 | 0.4851 | 0.00140 | 0.148 | ||
| 2 | 0 | 7 | 0 | 0.30090 | 0.4048 | 0.3269 | 0 | 1.292 | ||
| 3 | 0 | 9 | 0 | 0.17403 | 0.1269 | 0.2947 | 0 | 0.985 | ||
| 4 | 0 | 11 | 0 | 0.11759 | 0.0564 | 0.0677 | 0 | 1.190 | ||
| 5 | 0 | 13 | 0 | 0.11455 | 0.00304 | 0.0267 | 0 | 1.043 | ||
| 6 | 0 | 15 | 0 | 0.11426 | 0.000285 | 0.00242 | 0 | 1.153 | ||
| 7 | 0 | 17 | 0 | 0.11423 | 0.000027 | 0.00168 | 0 | 1.394 | ||
| 8 | 0 | 19 | 0 | 0.11423 | 5.552E-6 | 0.000478 | 0 | 1.413 | ||
| 9 | 0 | 21 | 0 | 0.11423 | 1.154E-6 | 0.000335 | 0 | 1.420 | ||
| 10 | 0 | 23 | 0 | 0.11423 | 2.405E-7 | 0.000105 | 0 | 1.427 | ||
| 11 | 0 | 25 | 0 | 0.11423 | 5.016E-8 | 0.000068 | 0 | 1.432 | ||
| 12 | 0 | 27 | 0 | 0.11423 | 1.047E-8 | 0.000023 | 0 | 1.436 | ||
| 13 | 0 | 29 | 0 | 0.11423 | 2.184E-9 | 0.000014 | 0 | 1.439 | ||
| 14 | 0 | 31 | 0 | 0.11423 | 4.56E-10 | 4.909E-6 | 0 | 1.442 |
There are 27 parameters in the bifactor model: nine for the loadings on the group factors Factor1–Factor3, nine for the loadings on the general factor FactorG, and nine for the variances of errors E1–E9. The optimization converges in 14 iterations without problems.
A fit summary table is shown in Output 29.26.6
The fit of this model is quite good. The chi-square value is 24.216, with df = 18 and p = 0.148. This is expected because the bifactor model has more parameters than the second-order factor model, which already has a good fit with fewer parameters.
Estimation results are shown in Output 29.26.7. Estimates are left uninterpreted because they are not the main interest of this example.
Output 29.26.7: Estimation Results
| Linear Equations | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| V1 | = | -0.4879 | Factor1 | + | 0.7679 | FactorG | + | 1.0000 | E1 | |
| V2 | = | -0.4523 | Factor1 | + | 0.7909 | FactorG | + | 1.0000 | E2 | |
| V3 | = | -0.4045 | Factor1 | + | 0.7536 | FactorG | + | 1.0000 | E3 | |
| V4 | = | 0.6140 | Factor2 | + | 0.6084 | FactorG | + | 1.0000 | E4 | |
| V5 | = | 0.5058 | Factor2 | + | 0.5973 | FactorG | + | 1.0000 | E5 | |
| V6 | = | 0.3943 | Factor2 | + | 0.5718 | FactorG | + | 1.0000 | E6 | |
| V7 | = | -0.7273 | Factor3 | + | 0.5669 | FactorG | + | 1.0000 | E7 | |
| V8 | = | -0.2468 | Factor3 | + | 0.6623 | FactorG | + | 1.0000 | E8 | |
| V9 | = | -0.4091 | Factor3 | + | 0.5300 | FactorG | + | 1.0000 | E9 | |
One might ask whether this bifactor (hierarchical) model provides a significantly better fit than the previous second-order model. Can one use a chi-square difference test for nested models to answer this question? The answer is yes.
Although it is not obvious that the previous second-order factor model is nested within the current bifactor model, a general nested relationship between the higher-order factor and the hierarchical factor model is formally proved by Yung, Thissen, and McLeod (1999). Therefore, a chi-square difference test can be conducted using the following DATA step:
data _null_; df0 = 24; chi0 = 38.1963; df1 = 18; chi1 = 24.2163; diff = chi0-chi1; p = 1.-probchi(chi0-chi1,df0-df1); put 'Chi-square difference = ' diff; put 'p-value = ' p; run;
The results are shown in the following:
The chi-square difference is 13.98, with df = 6 and p = 0.02986. If  -level is set at 0.05, the bifactor model indicates a significantly better fit. But if
-level is set at 0.05, the bifactor model indicates a significantly better fit. But if  -level is set at 0.01, statistically the two models fit equally well to the data.
-level is set at 0.01, statistically the two models fit equally well to the data.
In the next section, it is demonstrated that the second-order factor model is indeed nested within the bifactor model, and hence the chi-square test conducted in the previous section is justified. In addition, through the demonstration of the nested relationship between the two classes of models, you can see how some parameter constraints in structural equation model can be set up in PROC CALIS.
For some practical researchers, the technical details involved in the next section might not be of interest and therefore could be skipped.
A Constrained Bifactor Model and Its Equivalence to the Second-Order Factor Model
To demonstrate that the second-order factor model is indeed nested within the bifactor model, a constrained bifactor model is fitted in this section. This constrained bifactor model is essentially the same as the preceding bifactor model, but with additional constraints on the factor loadings. Hence, the constrained bifactor model is nested within the unconstrained bifactor model.
Furthermore, if it can be shown that the constrained bifactor model is equivalent to the previous second-order factor, then the second-order factor model must also be nested within the unconstrained bifactor model. As a result, it justifies the chi-square difference test conducted in the previous section.
The construction of such a constrained bifactor model is based on Yung, Thissen, and McLeod (1999). In the following statements, a constrained bifactor model is specified.
proc calis corr data=Thurst method=max nobs=213 nose nostand;
lineqs
V1 = X11 * Factor1 + X1g * FactorG + E1,
V2 = X21 * Factor1 + X2g * FactorG + E2,
V3 = X31 * Factor1 + X3g * FactorG + E3,
V4 = X42 * Factor2 + X4g * FactorG + E4,
V5 = X52 * Factor2 + X5g * FactorG + E5,
V6 = X62 * Factor2 + X6g * FactorG + E6,
V7 = X73 * Factor3 + X7g * FactorG + E7,
V8 = X83 * Factor3 + X8g * FactorG + E8,
V9 = X93 * Factor3 + X9g * FactorG + E9;
variance
Factor1-Factor3 = 3 * 1.,
FactorG = 1. ,
E1-E9 = U1-U9;
cov
Factor1-Factor3 FactorG = 6 * 0.;
bounds
0. <= U1-U9;
fitindex ON(ONLY)=[chisq df probchi];
parameters p1 (.5) p2 (.5) p3 (.5);
/* Proportionality constraints */
X1g = p1 * X11;
X2g = p1 * X21;
X3g = p1 * X31;
X4g = p2 * X42;
X5g = p2 * X52;
X6g = p2 * X62;
X7g = p3 * X73;
X8g = p3 * X83;
X9g = p3 * X93;
run;
In this constrained model, you add a PARAMETERS
statement and nine SAS programming statements
to the previous bifactor model. In the PARAMETERS
statement, three new independent parameters are added: p1, p2, and p3. These parameters represent the proportions that constrain the factor loadings of the observed variables on the group factors
Factor1–Factor3 and the general factor FactorG. They are all free parameters and have initial values at 0.5. The next nine SAS programming statements
represent the proportionality constraints imposed. For example, X1g–X3g are now dependent parameters expressed as functions of p1, X11, X21, and X31. Adding three new parameters (in the PARAMETERS
statement) and redefining nine original parameters as dependent (in the SAS programming statements
) is equivalent to adding six (=9-3) constraints to the original bifactor model. Mathematically, the additional statements
in specifying the constrained bifactor model realizes the following six constraints:
![\[ \frac{\mbox{X1g}}{\mbox{X11}} = \frac{\mbox{X2g}}{\mbox{X21}} = \frac{\mbox{X3g}}{\mbox{X31}} \]](images/statug_calis1015.png)
![\[ \frac{\mbox{X4g}}{\mbox{X42}} = \frac{\mbox{X5g}}{\mbox{X52}} = \frac{\mbox{X6g}}{\mbox{X62}} \]](images/statug_calis1016.png)
![\[ \frac{\mbox{X7g}}{\mbox{X73}} = \frac{\mbox{X8g}}{\mbox{X83}} = \frac{\mbox{X9g}}{\mbox{X93}} \]](images/statug_calis1017.png)
Obviously, with these six constraints the current constrained bifactor model is nested within the unconstrained version. What remains to be shown is that this constrained bifactor model is indeed equivalent to the previous second-order factor model. If so, the second-order factor model is also nested within the unconstrained bifactor model. One evidence for the equivalence of the current constrained bifactor model and the second-order factor model is from the fit summary table shown in Output 29.26.10. But first, it is also useful to consider the optimization information of the constrained bifactor model, which is shown in Output 29.26.9.
Output 29.26.9: Optimization
| Iteration | Restarts | Function Calls |
Active Constraints |
Objective Function |
Objective Function Change |
Max Abs Gradient Element |
Lambda | Ratio Between Actual and Predicted Change |
||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | * | 0 | 4 | 0 | 4.42090 | 2.4082 | 1.5979 | 0.195 | 0.121 | |
| 2 | * | 0 | 6 | 0 | 2.42951 | 1.9914 | 2.4449 | 0.195 | 1.700 | |
| 3 | * | 0 | 8 | 0 | 1.52546 | 0.9040 | 2.1675 | 0.781 | 1.657 | |
| 4 | * | 0 | 10 | 0 | 0.86547 | 0.6600 | 1.2570 | 0.781 | 1.552 | |
| 5 | * | 0 | 12 | 0 | 0.50425 | 0.3612 | 0.4075 | 0.781 | 1.351 | |
| 6 | * | 0 | 14 | 0 | 0.41864 | 0.0856 | 1.1698 | 0.195 | 0.216 | |
| 7 | * | 0 | 16 | 0 | 0.28298 | 0.1357 | 0.2355 | 0.0488 | 0.983 | |
| 8 | 0 | 19 | 0 | 0.27010 | 0.0129 | 0.9602 | 0.00098 | 0.327 | ||
| 9 | 0 | 21 | 0 | 0.21798 | 0.0521 | 0.2433 | 0 | 0.751 | ||
| 10 | * | 0 | 23 | 0 | 0.20781 | 0.0102 | 0.0373 | 0.0488 | 0.943 | |
| 11 | * | 0 | 26 | 0 | 0.20251 | 0.00530 | 0.0273 | 0.0918 | 1.064 | |
| 12 | 0 | 28 | 0 | 0.19176 | 0.0108 | 0.0718 | 0.0515 | 1.008 | ||
| 13 | 0 | 30 | 0 | 0.18575 | 0.00601 | 0.1407 | 0.00393 | 0.562 | ||
| 14 | 0 | 32 | 0 | 0.18024 | 0.00551 | 0.0224 | 0 | 0.921 | ||
| 15 | 0 | 34 | 0 | 0.18017 | 0.000064 | 0.00161 | 0 | 1.067 | ||
| 16 | 0 | 36 | 0 | 0.18017 | 2.357E-6 | 0.000538 | 0 | 1.344 | ||
| 17 | 0 | 38 | 0 | 0.18017 | 3.389E-7 | 0.000216 | 0 | 1.380 | ||
| 18 | 0 | 40 | 0 | 0.18017 | 5.146E-8 | 0.000075 | 0 | 1.389 | ||
| 19 | 0 | 42 | 0 | 0.18017 | 7.886E-9 | 0.000031 | 0 | 1.391 | ||
| 20 | 0 | 44 | 0 | 0.18017 | 1.211E-9 | 0.000012 | 0 | 1.392 |
As shown Output 29.26.9, there are 21 independent parameters in the constrained bifactor model for the 45 "Functions (Observations)." These numbers match those of the second-order factor model exactly. The optimization shows some problems in initial iterations. The iteration numbers with asterisks indicate that the Hessian matrix is not positive definite in those iterations. But as long as the final converged iteration is not marked with an asterisk, the problems exhibited in early iterations do not raise any concern, as in the current case. Next, the fit summary is shown in Output 29.26.10.
In Output 29.26.10, the chi-square value in the fit summary table is 38.196, with df = 24, and p = 0.033. Again, these numbers match those of the second-order factor model exactly. These matches (same model fit with the same number of parameters) are necessary (but not sufficient) to show that the constrained bifactor model is equivalent to the second-order model. Stronger evidence is now presented.
In Output 29.26.11, estimation results of the constrained bifactor model are shown.
Output 29.26.11: Estimation Results
| Linear Equations | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| V1 | = | -0.5151 | Factor1 | + | 0.7437 | FactorG | + | 1.0000 | E1 | |
| V2 | = | -0.5203 | Factor1 | + | 0.7512 | FactorG | + | 1.0000 | E2 | |
| V3 | = | -0.4874 | Factor1 | + | 0.7038 | FactorG | + | 1.0000 | E3 | |
| V4 | = | 0.5211 | Factor2 | + | 0.6534 | FactorG | + | 1.0000 | E4 | |
| V5 | = | 0.4971 | Factor2 | + | 0.6232 | FactorG | + | 1.0000 | E5 | |
| V6 | = | 0.4381 | Factor2 | + | 0.5493 | FactorG | + | 1.0000 | E6 | |
| V7 | = | 0.4524 | Factor3 | + | 0.6364 | FactorG | + | 1.0000 | E7 | |
| V8 | = | 0.4173 | Factor3 | + | 0.5869 | FactorG | + | 1.0000 | E8 | |
| V9 | = | 0.4076 | Factor3 | + | 0.5734 | FactorG | + | 1.0000 | E9 | |
According to Yung, Thissen, and McLeod (1999), two models are equivalent if there is a one-to-one correspondence of the parameters in the models. This fact is illustrated for the constrained bifactor model and the second-order factor model.
First, the error variances for E1–E9 in the second-order factor model are transformed directly (using an identity map) to that of the bifactor models. The nine
error variances in Output 29.26.4 for the second-order factor model match those of the constrained bifactor model exactly in Output 29.26.11. In addition, the variances of factors are fixed at one in both models. The error variances and the factor loadings at both
factor levels in Output 29.26.4 for the second-order factor model are now transformed to yield the loading estimates in the constrained bifactor model.
Denote 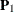 as the first-order factor loading matrix,
as the first-order factor loading matrix, 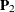 as the second-order factor loading matrix, and
as the second-order factor loading matrix, and 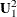 be the matrix of variances for disturbances. That is, for the second-order factor model,
be the matrix of variances for disturbances. That is, for the second-order factor model,
![\[ \mb{P}_1 = \left( \begin{array}{ccc} 0.9047 & 0 & 0 \\ 0.9138 & 0 & 0 \\ 0.8561 & 0 & 0 \\ 0 & 0.8358 & 0 \\ 0 & 0.7972 & 0 \\ 0 & 0.7026 & 0 \\ 0 & 0 & 0.7808 \\ 0 & 0 & 0.7202 \\ 0 & 0 & 0.7035 \\ \end{array} \right) \]](images/statug_calis1020.png)
![\[ \mb{P}_2 = \left( \begin{array}{c} 0.8221 \\ 0.7818 \\ 0.8150 \\ \end{array} \right) \]](images/statug_calis1021.png)
![\[ \mb{U}_1^2 = \left( \begin{array}{ccc} 0.3242 & 0 & 0 \\ 0 & 0.3888 & 0 \\ 0 & 0 & 0.3358 \\ \end{array} \right) \]](images/statug_calis1022.png)
According to Yung, Thissen, and McLeod (1999), the transformation to obtain the estimates in the equivalent constrained bifactor model is:
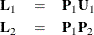
where 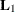 is the matrix of the first-layer factor loadings (that is, loadings on group factors
is the matrix of the first-layer factor loadings (that is, loadings on group factors Factor1–Factor3), and 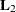 is the matrix of the second-layer factor loadings (that is, loadings on FactorG) in the constrained bifactor model. Carrying
out the matrix calculations for
is the matrix of the second-layer factor loadings (that is, loadings on FactorG) in the constrained bifactor model. Carrying
out the matrix calculations for 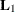 and
and 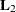 shows that:
shows that:
![\[ \mb{L}_1 = \left( \begin{array}{ccc} 0.5151 & 0 & 0 \\ 0.5203 & 0 & 0 \\ 0.4875 & 0 & 0 \\ 0 & 0.5212 & 0 \\ 0 & 0.4971 & 0 \\ 0 & 0.4381 & 0 \\ 0 & 0 & 0.4525 \\ 0 & 0 & 0.4173 \\ 0 & 0 & 0.4077 \\ \end{array} \right) \]](images/statug_calis1026.png)
![\[ \mb{L}_2 = \left( \begin{array}{c} 0.7438 \\ 0.7512 \\ 0.7038 \\ 0.6534 \\ 0.6232 \\ 0.5493 \\ 0.6364 \\ 0.5870 \\ 0.5734 \\ \end{array} \right) \]](images/statug_calis1027.png)
With very minor numerical differences and ignorable sign changes, these transformation results match the estimated loadings observed in Output 29.26.11 for the constrained bifactor model. Therefore, the second-order factor model is shown to be equivalent to the constrained bifactor model, and hence is nested within the unconstrained bifactor model.