The CALIS Procedure
-
Overview

-
Getting Started

-
Syntax
 Classes of Statements in PROC CALISSingle-Group Analysis SyntaxMultiple-Group Multiple-Model Analysis SyntaxPROC CALIS StatementBOUNDS StatementBY StatementCOSAN StatementCOV StatementDETERM StatementEFFPART StatementFACTOR StatementFITINDEX StatementFREQ StatementGROUP StatementLINCON StatementLINEQS StatementLISMOD StatementLMTESTS StatementMATRIX StatementMEAN StatementMODEL StatementMSTRUCT StatementNLINCON StatementNLOPTIONS StatementOUTFILES StatementPARAMETERS StatementPARTIAL StatementPATH StatementPATHDIAGRAM StatementPCOV StatementPVAR StatementRAM StatementREFMODEL StatementRENAMEPARM StatementSAS Programming StatementsSIMTESTS StatementSTD StatementSTRUCTEQ StatementTESTFUNC StatementVAR StatementVARIANCE StatementVARNAMES StatementWEIGHT Statement
Classes of Statements in PROC CALISSingle-Group Analysis SyntaxMultiple-Group Multiple-Model Analysis SyntaxPROC CALIS StatementBOUNDS StatementBY StatementCOSAN StatementCOV StatementDETERM StatementEFFPART StatementFACTOR StatementFITINDEX StatementFREQ StatementGROUP StatementLINCON StatementLINEQS StatementLISMOD StatementLMTESTS StatementMATRIX StatementMEAN StatementMODEL StatementMSTRUCT StatementNLINCON StatementNLOPTIONS StatementOUTFILES StatementPARAMETERS StatementPARTIAL StatementPATH StatementPATHDIAGRAM StatementPCOV StatementPVAR StatementRAM StatementREFMODEL StatementRENAMEPARM StatementSAS Programming StatementsSIMTESTS StatementSTD StatementSTRUCTEQ StatementTESTFUNC StatementVAR StatementVARIANCE StatementVARNAMES StatementWEIGHT Statement -
Details
 Input Data SetsOutput Data SetsDefault Analysis Type and Default ParameterizationThe COSAN ModelThe FACTOR ModelThe LINEQS ModelThe LISMOD Model and SubmodelsThe MSTRUCT ModelThe PATH ModelThe RAM ModelNaming Variables and ParametersSetting Constraints on ParametersAutomatic Variable SelectionPath Diagrams: Layout Algorithms, Default Settings, and CustomizationEstimation CriteriaRelationships among Estimation CriteriaGradient, Hessian, Information Matrix, and Approximate Standard ErrorsCounting the Degrees of FreedomAssessment of FitCase-Level Residuals, Outliers, Leverage Observations, and Residual DiagnosticsLatent Variable ScoresTotal, Direct, and Indirect EffectsStandardized SolutionsModification IndicesMissing Values and the Analysis of Missing PatternsMeasures of Multivariate KurtosisInitial EstimatesUse of Optimization TechniquesComputational ProblemsDisplayed OutputODS Table NamesODS Graphics
Input Data SetsOutput Data SetsDefault Analysis Type and Default ParameterizationThe COSAN ModelThe FACTOR ModelThe LINEQS ModelThe LISMOD Model and SubmodelsThe MSTRUCT ModelThe PATH ModelThe RAM ModelNaming Variables and ParametersSetting Constraints on ParametersAutomatic Variable SelectionPath Diagrams: Layout Algorithms, Default Settings, and CustomizationEstimation CriteriaRelationships among Estimation CriteriaGradient, Hessian, Information Matrix, and Approximate Standard ErrorsCounting the Degrees of FreedomAssessment of FitCase-Level Residuals, Outliers, Leverage Observations, and Residual DiagnosticsLatent Variable ScoresTotal, Direct, and Indirect EffectsStandardized SolutionsModification IndicesMissing Values and the Analysis of Missing PatternsMeasures of Multivariate KurtosisInitial EstimatesUse of Optimization TechniquesComputational ProblemsDisplayed OutputODS Table NamesODS Graphics -
Examples
 Estimating Covariances and CorrelationsEstimating Covariances and Means SimultaneouslyTesting Uncorrelatedness of VariablesTesting Covariance PatternsTesting Some Standard Covariance Pattern HypothesesLinear Regression ModelMultivariate Regression ModelsMeasurement Error ModelsTesting Specific Measurement Error ModelsMeasurement Error Models with Multiple PredictorsMeasurement Error Models Specified As Linear EquationsConfirmatory Factor ModelsConfirmatory Factor Models: Some VariationsResidual Diagnostics and Robust EstimationThe Full Information Maximum Likelihood MethodComparing the ML and FIML EstimationPath Analysis: Stability of AlienationSimultaneous Equations with Mean Structures and Reciprocal PathsFitting Direct Covariance StructuresConfirmatory Factor Analysis: Cognitive AbilitiesTesting Equality of Two Covariance Matrices Using a Multiple-Group AnalysisTesting Equality of Covariance and Mean Matrices between Independent GroupsIllustrating Various General Modeling LanguagesTesting Competing Path Models for the Career Aspiration DataFitting a Latent Growth Curve ModelHigher-Order and Hierarchical Factor ModelsLinear Relations among Factor LoadingsMultiple-Group Model for Purchasing BehaviorFitting the RAM and EQS Models by the COSAN Modeling LanguageSecond-Order Confirmatory Factor AnalysisLinear Relations among Factor Loadings: COSAN Model SpecificationOrdinal Relations among Factor LoadingsLongitudinal Factor Analysis
Estimating Covariances and CorrelationsEstimating Covariances and Means SimultaneouslyTesting Uncorrelatedness of VariablesTesting Covariance PatternsTesting Some Standard Covariance Pattern HypothesesLinear Regression ModelMultivariate Regression ModelsMeasurement Error ModelsTesting Specific Measurement Error ModelsMeasurement Error Models with Multiple PredictorsMeasurement Error Models Specified As Linear EquationsConfirmatory Factor ModelsConfirmatory Factor Models: Some VariationsResidual Diagnostics and Robust EstimationThe Full Information Maximum Likelihood MethodComparing the ML and FIML EstimationPath Analysis: Stability of AlienationSimultaneous Equations with Mean Structures and Reciprocal PathsFitting Direct Covariance StructuresConfirmatory Factor Analysis: Cognitive AbilitiesTesting Equality of Two Covariance Matrices Using a Multiple-Group AnalysisTesting Equality of Covariance and Mean Matrices between Independent GroupsIllustrating Various General Modeling LanguagesTesting Competing Path Models for the Career Aspiration DataFitting a Latent Growth Curve ModelHigher-Order and Hierarchical Factor ModelsLinear Relations among Factor LoadingsMultiple-Group Model for Purchasing BehaviorFitting the RAM and EQS Models by the COSAN Modeling LanguageSecond-Order Confirmatory Factor AnalysisLinear Relations among Factor Loadings: COSAN Model SpecificationOrdinal Relations among Factor LoadingsLongitudinal Factor Analysis - References
Example 29.30 Second-Order Confirmatory Factor Analysis
A second-order confirmatory factor analysis model is applied to a correlation matrix of Thurstone reported by McDonald (1985). The data set is shown in the following DATA step:
data Thurst(TYPE=CORR);
title "Example of THURSTONE resp. McDONALD (1985, p.57, p.105)";
_TYPE_ = 'CORR'; Input _NAME_ $ Obs1-Obs9;
label obs1='Sentences' obs2='Vocabulary' obs3='Sentence Completion'
obs4='First Letters' obs5='Four-letter Words' obs6='Suffices'
obs7='Letter series' obs8='Pedigrees' obs9='Letter Grouping';
datalines;
obs1 1. . . . . . . . .
obs2 .828 1. . . . . . . .
obs3 .776 .779 1. . . . . . .
obs4 .439 .493 .460 1. . . . . .
obs5 .432 .464 .425 .674 1. . . . .
obs6 .447 .489 .443 .590 .541 1. . . .
obs7 .447 .432 .401 .381 .402 .288 1. . .
obs8 .541 .537 .534 .350 .367 .320 .555 1. .
obs9 .380 .358 .359 .424 .446 .325 .598 .452 1.
;
Using the LINEQS modeling language, you specify the three-term second-order factor analysis model in the following statements:
proc calis data=Thurst nobs=213 corr nose; lineqs obs1 = x1 * f1 + e1, obs2 = x2 * f1 + e2, obs3 = x3 * f1 + e3, obs4 = x4 * f2 + e4, obs5 = x5 * f2 + e5, obs6 = x6 * f2 + e6, obs7 = x7 * f3 + e7, obs8 = x8 * f3 + e8, obs9 = x9 * f3 + e9, f1 = x10 * f4 + e10, f2 = x11 * f4 + e11, f3 = x12 * f4 + e12; variance f4 = 1., e1-e9 = u1-u9, e10-e12 = 3 * 1.; bounds 0. <= u1-u9; run;
In the PROC CALIS statement, you specify the data set in the DATA= option and the number of observations in the NOBS= option. With the CORR option, you request the correlations be analyzed. You use the NOSE option to suppress the computation of standard error estimates.
In the LINEQS statement, the first-order loadings for the three factors, f1, f2, and f3, each refer to three variables, X1–X3, X4–X6, and X7–X9, respectively. One second-order factor, f4, reflects the correlations among the three first-order factors, f1, f2, and f3.
In the VARIANCE statement, you fix the variance of f4 to 1.0 for identification. The variances of error terms e1–e9 are free parameters u1–u9. The error variances for the three first-order factors are also fixed at 1.0 for identification purposes.
You also specify the boundary constraints for the error variance parameters u1–u9. You require them to be positive in the estimation.
Output 29.30.1 shows the estimation results.
Output 29.30.1: Estimation Results of the Second-Order Factor Model for Thurstone Data: LINEQS Model
| Linear Equations | |||||||
|---|---|---|---|---|---|---|---|
| Obs1 | = | 0.5151 | f1 | + | 1.0000 | e1 | |
| Obs2 | = | 0.5203 | f1 | + | 1.0000 | e2 | |
| Obs3 | = | 0.4874 | f1 | + | 1.0000 | e3 | |
| Obs4 | = | 0.5211 | f2 | + | 1.0000 | e4 | |
| Obs5 | = | 0.4971 | f2 | + | 1.0000 | e5 | |
| Obs6 | = | 0.4381 | f2 | + | 1.0000 | e6 | |
| Obs7 | = | 0.4524 | f3 | + | 1.0000 | e7 | |
| Obs8 | = | 0.4173 | f3 | + | 1.0000 | e8 | |
| Obs9 | = | 0.4076 | f3 | + | 1.0000 | e9 | |
| f1 | = | 1.4438 | f4 | + | 1.0000 | e10 | |
| f2 | = | 1.2538 | f4 | + | 1.0000 | e11 | |
| f3 | = | 1.4065 | f4 | + | 1.0000 | e12 | |
Alternatively, you can use the COSAN model specification for analyzing the same data set. First, under the second-order factor model, the covariance structures of the observed variables can be derived as
![\[ \bSigma = \mb{F1} * \mb{F2} * \mb{P} * \mb{F2}^{\prime } * \mb{F1}^{\prime } + \mb{F1} * \mb{U2} * \mb{F1}^{\prime } + \mb{U1} \]](images/statug_calis1078.png)
where 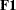 is the 9
is the 9  3 first-order loading matrix for the observed variables,
3 first-order loading matrix for the observed variables, 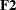 is the 3
is the 3  1 second-order loading matrix for the first-order factors,
1 second-order loading matrix for the first-order factors, 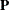 is the 1
is the 1  1 covariance matrix for the second-order factor
1 covariance matrix for the second-order factor f4,  is the 3
is the 3  3 error covariance matrix of the first-order factors
3 error covariance matrix of the first-order factors f1–f3 (or the covariance matrix of the error terms e10–12), and  is the 9
is the 9  9 error covariance matrix for the observed variables (or the covariance matrix of the error terms
9 error covariance matrix for the observed variables (or the covariance matrix of the error terms e1–9).
Matrix 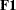 contains the loading parameters
contains the loading parameters x1–x9 and matrix 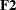 contains the loading parameters
contains the loading parameters x10–x12. Because there is only one second-order factor f4 in the model, matrix 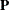 is a scalar, which is a fixed constant 1 in the LINEQS model. Matrix
is a scalar, which is a fixed constant 1 in the LINEQS model. Matrix  is an identity matrix because all error variances are fixed at 1 and they are not correlated. Matrix
is an identity matrix because all error variances are fixed at 1 and they are not correlated. Matrix  is a diagonal matrix that contains the parameters
is a diagonal matrix that contains the parameters u1–u9. Given this information, you can use the following statements to specify the second-order factor model as a COSAN model:
proc calis data=Thurst nobs=213 corr nose;
cosan
var = obs1-obs9,
F1(3) * F2(1) * P(1,IDE) + F1(3) * U2(3,IDE) + U1(9,DIA);
matrix F1
[1 , @1] = x1-x3,
[4 , @2] = x4-X6,
[7 , @3] = x7-x9;
matrix F2
[ ,1] = x10-x12;
matrix U1
[1,1] = u1-u9;
bounds
0. <= u1-u9;
vnames
F1 = [f1 f2 f3],
F2 = [f4],
U1 = [e1-e9];
run;
In the PROC CALIS statement, you specify the observed variables in the VAR= option and the covariance structures for the observed variables. In the terms of the covariance structure formula, you need to specify the expressions only up the central symmetric matrices. The latter parts of these expressions are redundant and can be generated automatically by PROC CALIS, as shown in Output 29.30.2.
Output 29.30.2: The Covariance Structures and Model Matrices of the Second-Order Factor Model: COSAN Model
Output 29.30.2 shows that the intended covariance structures for the observed variables are being analyzed. The matrix types are shown next.
Matrix 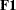 is a rectangular matrix and matrix
is a rectangular matrix and matrix 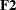 is a vector, although they have the default general (GEN) matrix type. Matrices
is a vector, although they have the default general (GEN) matrix type. Matrices 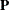 and
and  are fixed identity (IDE) matrices in the model. For these two matrices, you do not need to specify any of their elements
by using the MATRIX statement because they are already well-defined with the IDE type. Lastly, matrix
are fixed identity (IDE) matrices in the model. For these two matrices, you do not need to specify any of their elements
by using the MATRIX statement because they are already well-defined with the IDE type. Lastly, matrix  is a diagonal (DIA) matrix in the model.
is a diagonal (DIA) matrix in the model.
Output 29.30.3 shows the estimates of the first-order factor loading matrix 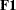 .
.
Output 29.30.3: Estimation of the 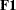 Matrix of the Second-Order Factor Model: COSAN Model
Matrix of the Second-Order Factor Model: COSAN Model
In the MATRIX statement for 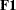 , you specify the pattern of the loadings. In the first entry of the MATRIX statement, you specify the loadings in the following
elements:
, you specify the pattern of the loadings. In the first entry of the MATRIX statement, you specify the loadings in the following
elements: [1,1], [2,1], and [3,1]. They are free parameters x1–x3, respectively. Notice that the @ sign is necessary in the first entry because the elements being defined would have been [1,1], [2,2], and [3,3] otherwise. The @ sign fixes the column number to 1. See the MATRIX
statement for more details about the notation. Similarly, you define the other clusters of loading in the second and third
entries in the MATRIX statement for 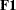 . This explains the pattern of factor loadings in Output 29.30.3. These loading estimates
. This explains the pattern of factor loadings in Output 29.30.3. These loading estimates x1–x9 match those by the LINEQS model specification, as shown in Output 29.30.1.
Output 29.30.3 shows the estimates of the second-order factor loading matrix 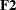 .
.
Output 29.30.4: Estimation of the 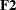 Matrix of the Second-Order Factor Model: COSAN Model
Matrix of the Second-Order Factor Model: COSAN Model
In the MATRIX statement for 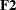 , you do not specify the row numbers in the
, you do not specify the row numbers in the [ ,1] specification. PROC CALIS interprets this as stating that all the valid elements in the first column are being specified
in the parameter list. In the current example, this means that elements ![$\mb{F2}[1,1]$](images/statug_calis1083.png) ,
, ![$\mb{F2}[2,1]$](images/statug_calis1084.png) , and
, and ![$\mb{F2}[3,1]$](images/statug_calis1085.png) are filled with the free parameters
are filled with the free parameters x10, x11, and x12, respectively. Output 29.30.3 shows these specification and the corresponding estimates, which match those of the LINEQS model specification, as shown
in Output 29.30.1.
Output 29.30.5 shows the estimates of the error covariance matrix  .
.
Output 29.30.5: Estimation of the  Matrix of the Second-Order Factor Model: COSAN Model
Matrix of the Second-Order Factor Model: COSAN Model
| Model Matrix U1 | |||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (9 x 9 Diagonal Matrix) | |||||||||||||||||||||||||||
| e1 | e2 | e3 | e4 | e5 | e6 | e7 | e8 | e9 | |||||||||||||||||||
| e1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
| e2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
| e3 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
| e4 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
| e5 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
| e6 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
| e7 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
| e8 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
| e9 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
In the MATRIX statement for  , you specify the diagonal elements of the matrix by using the starting element at
, you specify the diagonal elements of the matrix by using the starting element at [1,1]. The parameter assignment proceeds to [2,2], [3,3] and so on such that all the trailing parameters u1–u9 are filled. This means that the last element ![$\mb{U1}[9,9]$](images/statug_calis1086.png) is a free parameter named
is a free parameter named u9. Output 29.30.5 confirms this intended pattern. Again, all these error variance estimates match those by the LINEQS model specification,
as shown in Output 29.30.1.