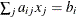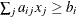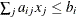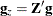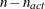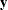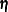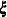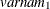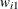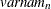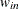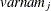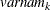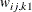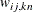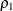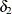The CALIS Procedure
-
Overview

-
Getting Started

-
Syntax
 Classes of Statements in PROC CALISSingle-Group Analysis SyntaxMultiple-Group Multiple-Model Analysis SyntaxPROC CALIS StatementBOUNDS StatementBY StatementCOSAN StatementCOV StatementDETERM StatementEFFPART StatementFACTOR StatementFITINDEX StatementFREQ StatementGROUP StatementLINCON StatementLINEQS StatementLISMOD StatementLMTESTS StatementMATRIX StatementMEAN StatementMODEL StatementMSTRUCT StatementNLINCON StatementNLOPTIONS StatementOUTFILES StatementPARAMETERS StatementPARTIAL StatementPATH StatementPATHDIAGRAM StatementPCOV StatementPVAR StatementRAM StatementREFMODEL StatementRENAMEPARM StatementSAS Programming StatementsSIMTESTS StatementSTD StatementSTRUCTEQ StatementTESTFUNC StatementVAR StatementVARIANCE StatementVARNAMES StatementWEIGHT Statement
Classes of Statements in PROC CALISSingle-Group Analysis SyntaxMultiple-Group Multiple-Model Analysis SyntaxPROC CALIS StatementBOUNDS StatementBY StatementCOSAN StatementCOV StatementDETERM StatementEFFPART StatementFACTOR StatementFITINDEX StatementFREQ StatementGROUP StatementLINCON StatementLINEQS StatementLISMOD StatementLMTESTS StatementMATRIX StatementMEAN StatementMODEL StatementMSTRUCT StatementNLINCON StatementNLOPTIONS StatementOUTFILES StatementPARAMETERS StatementPARTIAL StatementPATH StatementPATHDIAGRAM StatementPCOV StatementPVAR StatementRAM StatementREFMODEL StatementRENAMEPARM StatementSAS Programming StatementsSIMTESTS StatementSTD StatementSTRUCTEQ StatementTESTFUNC StatementVAR StatementVARIANCE StatementVARNAMES StatementWEIGHT Statement -
Details
 Input Data SetsOutput Data SetsDefault Analysis Type and Default ParameterizationThe COSAN ModelThe FACTOR ModelThe LINEQS ModelThe LISMOD Model and SubmodelsThe MSTRUCT ModelThe PATH ModelThe RAM ModelNaming Variables and ParametersSetting Constraints on ParametersAutomatic Variable SelectionPath Diagrams: Layout Algorithms, Default Settings, and CustomizationEstimation CriteriaRelationships among Estimation CriteriaGradient, Hessian, Information Matrix, and Approximate Standard ErrorsCounting the Degrees of FreedomAssessment of FitCase-Level Residuals, Outliers, Leverage Observations, and Residual DiagnosticsLatent Variable ScoresTotal, Direct, and Indirect EffectsStandardized SolutionsModification IndicesMissing Values and the Analysis of Missing PatternsMeasures of Multivariate KurtosisInitial EstimatesUse of Optimization TechniquesComputational ProblemsDisplayed OutputODS Table NamesODS Graphics
Input Data SetsOutput Data SetsDefault Analysis Type and Default ParameterizationThe COSAN ModelThe FACTOR ModelThe LINEQS ModelThe LISMOD Model and SubmodelsThe MSTRUCT ModelThe PATH ModelThe RAM ModelNaming Variables and ParametersSetting Constraints on ParametersAutomatic Variable SelectionPath Diagrams: Layout Algorithms, Default Settings, and CustomizationEstimation CriteriaRelationships among Estimation CriteriaGradient, Hessian, Information Matrix, and Approximate Standard ErrorsCounting the Degrees of FreedomAssessment of FitCase-Level Residuals, Outliers, Leverage Observations, and Residual DiagnosticsLatent Variable ScoresTotal, Direct, and Indirect EffectsStandardized SolutionsModification IndicesMissing Values and the Analysis of Missing PatternsMeasures of Multivariate KurtosisInitial EstimatesUse of Optimization TechniquesComputational ProblemsDisplayed OutputODS Table NamesODS Graphics -
Examples
 Estimating Covariances and CorrelationsEstimating Covariances and Means SimultaneouslyTesting Uncorrelatedness of VariablesTesting Covariance PatternsTesting Some Standard Covariance Pattern HypothesesLinear Regression ModelMultivariate Regression ModelsMeasurement Error ModelsTesting Specific Measurement Error ModelsMeasurement Error Models with Multiple PredictorsMeasurement Error Models Specified As Linear EquationsConfirmatory Factor ModelsConfirmatory Factor Models: Some VariationsResidual Diagnostics and Robust EstimationThe Full Information Maximum Likelihood MethodComparing the ML and FIML EstimationPath Analysis: Stability of AlienationSimultaneous Equations with Mean Structures and Reciprocal PathsFitting Direct Covariance StructuresConfirmatory Factor Analysis: Cognitive AbilitiesTesting Equality of Two Covariance Matrices Using a Multiple-Group AnalysisTesting Equality of Covariance and Mean Matrices between Independent GroupsIllustrating Various General Modeling LanguagesTesting Competing Path Models for the Career Aspiration DataFitting a Latent Growth Curve ModelHigher-Order and Hierarchical Factor ModelsLinear Relations among Factor LoadingsMultiple-Group Model for Purchasing BehaviorFitting the RAM and EQS Models by the COSAN Modeling LanguageSecond-Order Confirmatory Factor AnalysisLinear Relations among Factor Loadings: COSAN Model SpecificationOrdinal Relations among Factor LoadingsLongitudinal Factor Analysis
Estimating Covariances and CorrelationsEstimating Covariances and Means SimultaneouslyTesting Uncorrelatedness of VariablesTesting Covariance PatternsTesting Some Standard Covariance Pattern HypothesesLinear Regression ModelMultivariate Regression ModelsMeasurement Error ModelsTesting Specific Measurement Error ModelsMeasurement Error Models with Multiple PredictorsMeasurement Error Models Specified As Linear EquationsConfirmatory Factor ModelsConfirmatory Factor Models: Some VariationsResidual Diagnostics and Robust EstimationThe Full Information Maximum Likelihood MethodComparing the ML and FIML EstimationPath Analysis: Stability of AlienationSimultaneous Equations with Mean Structures and Reciprocal PathsFitting Direct Covariance StructuresConfirmatory Factor Analysis: Cognitive AbilitiesTesting Equality of Two Covariance Matrices Using a Multiple-Group AnalysisTesting Equality of Covariance and Mean Matrices between Independent GroupsIllustrating Various General Modeling LanguagesTesting Competing Path Models for the Career Aspiration DataFitting a Latent Growth Curve ModelHigher-Order and Hierarchical Factor ModelsLinear Relations among Factor LoadingsMultiple-Group Model for Purchasing BehaviorFitting the RAM and EQS Models by the COSAN Modeling LanguageSecond-Order Confirmatory Factor AnalysisLinear Relations among Factor Loadings: COSAN Model SpecificationOrdinal Relations among Factor LoadingsLongitudinal Factor Analysis - References
Output Data Sets
OUTEST= Data Set
The OUTEST= (or OUTVAR=) data set is of TYPE=EST and contains the final parameter estimates, the gradient, the Hessian, and boundary and linear constraints. For METHOD= ML (with or without the ROBUST option), METHOD= FIML, METHOD= GLS, and METHOD= WLS, the OUTEST= data set also contains the approximate standard errors, the information matrix (crossproduct Jacobian), and the approximate covariance matrix of the parameter estimates ((generalized) inverse of the information matrix). If there are linear or nonlinear equality or active inequality constraints at the solution, the OUTEST= data set also contains Lagrange multipliers, the projected Hessian matrix, and the Hessian matrix of the Lagrange function.
The OUTEST= data set can be used to save the results of an optimization by PROC CALIS for another analysis with either PROC CALIS or another SAS procedure. Saving results to an OUTEST= data set is advised for expensive applications that cannot be repeated without considerable effort.
The OUTEST=
data set contains the BY variables, two character variables _TYPE_ and _NAME_, t numeric variables corresponding to the parameters used in the model, a numeric variable _RHS_ (right-hand side) that is used for the right-hand-side value 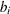 of a linear constraint or for the value
of a linear constraint or for the value 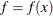 of the objective function at the final point
of the objective function at the final point 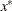 of the parameter space, and a numeric variable
of the parameter space, and a numeric variable _ITER_ that is set to zero for initial values, set to the iteration number for the OUTITER output, and set to missing for the result
output.
The _TYPE_ observations in Table 29.5 are available in the OUTEST=
data set, depending on the request.
Table 29.5: _TYPE_ Observations in the OUTEST= Data Set
|
|
Description |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
ACTBC |
If there are active boundary constraints at the solution
|
||||||||||
|
COV |
Contains the approximate covariance matrix of the parameter estimates; used in computing the approximate standard errors. |
||||||||||
|
COVRANK |
contains the rank of the covariance matrix of the parameter estimates. |
||||||||||
|
CRPJ_LF |
Contains the Hessian matrix of the Lagrange function (based on CRPJAC). |
||||||||||
|
CRPJAC |
Contains the approximate Hessian matrix used in the optimization process. This is the inverse of the information matrix. |
||||||||||
|
EQ |
If linear constraints are used, this observation contains the ith linear constraint |
||||||||||
|
GE |
If linear constraints are used, this observation contains the ith linear constraint |
||||||||||
|
GRAD |
Contains the gradient of the estimates. |
||||||||||
|
GRAD_LF |
Contains the gradient of the Lagrange function. The |
||||||||||
|
HESSIAN |
Contains the Hessian matrix. |
||||||||||
|
HESS_LF |
Contains the Hessian matrix of the Lagrange function (based on HESSIAN). |
||||||||||
|
INFORMAT |
Contains the information matrix of the parameter estimates (only for METHOD= ML, METHOD= GLS, or METHOD= WLS). |
||||||||||
|
INITGRAD |
Contains the gradient of the starting estimates. |
||||||||||
|
INITIAL |
Contains the starting values of the parameter estimates. |
||||||||||
|
JACNLC |
Contains the Jacobian of the nonlinear constraints evaluated at the final estimates. |
||||||||||
|
LAGM BC |
Contains Lagrange multipliers for masks and active boundary constraints.
|
||||||||||
|
LAGM LC |
Contains Lagrange multipliers for linear equality and active inequality constraints in pairs of observations containing the constraint number and the value of the Lagrange multiplier.
|
||||||||||
|
LAGM NLC |
contains Lagrange multipliers for nonlinear equality and active inequality constraints in pairs of observations that contain the constraint number and the value of the Lagrange multiplier.
|
||||||||||
|
LE |
If linear constraints are used, this observation contains the ith linear constraint |
||||||||||
|
LOWERBD |
If boundary constraints are used, this observation contains the lower bounds. Those parameters not subjected to lower bounds
contain missing values. The |
||||||||||
|
NACTBC |
All parameter variables contain the number |
||||||||||
|
NACTLC |
All parameter variables contain the number |
||||||||||
|
NLC_EQ |
Contains values and residuals of nonlinear constraints. The
|
||||||||||
|
NLDACTBC |
Contains the number of active boundary constraints at the solution |
||||||||||
|
NLDACTLC |
Contains the number of active linear constraints at the solution |
||||||||||
|
_NOBS_ |
Contains the number of observations. |
||||||||||
|
PARMS |
Contains the final parameter estimates. The |
||||||||||
|
PCRPJ_LF |
Contains the projected Hessian matrix of the Lagrange function (based on CRPJAC). |
||||||||||
|
PHESS_LF |
Contains the projected Hessian matrix of the Lagrange function (based on HESSIAN). |
||||||||||
|
PROJCRPJ |
Contains the projected Hessian matrix (based on CRPJAC). |
||||||||||
|
PROJGRAD |
If linear constraints are used in the estimation, this observation contains the |
||||||||||
|
PROJHESS |
Contains the projected Hessian matrix (based on HESSIAN). |
||||||||||
|
STDERR |
Contains approximate standard errors (only for METHOD= ML, METHOD= GLS, or METHOD= WLS). |
||||||||||
|
TERMINAT |
The |
||||||||||
|
UPPERBD |
If boundary constraints are used, this observation contains the upper bounds. Those parameters not subjected to upper bounds
contain missing values. The |
If the technique specified by the OMETHOD= option cannot be performed (for example, no feasible initial values can be computed or the function value or derivatives cannot be evaluated at the starting point), the OUTEST= data set can contain only some of the observations (usually only the PARMS and GRAD observations).
OUTMODEL= or OUTRAM= Data Set
The OUTMODEL= (or OUTRAM= ) data set is of TYPE=CALISMDL and contains the model specification, the computed parameter estimates, and the standard error estimates. This data set is intended to be reused as an INMODEL= data set to specify good initial values in a subsequent analysis by PROC CALIS.
The OUTMODEL= data set contains the following variables:
-
the BY variables, if any
-
an
_MDLNUM_variable for model numbers, if used -
a character variable
_TYPE_, which takes various values that indicate the type of model specification -
a character variable
_NAME_, which indicates the model type, parameter name, or variable name -
a character variable
_MATNR_, which indicates the matrix number (COSAN models only) -
a character variable
_VAR1_, which is the name or number of the first variable in the specification -
a character variable
_VAR2_, which is the name or number of the second variable in the specification -
a numerical variable
_ESTIM_for the final estimate of the parameter location -
a numerical variable
_STDERR_for the standard error estimate of the parameter location -
a numerical variable
_SDEST_for the final standardized estimate of the parameter location -
a numerical variable
_SDSE_for the standard error of the standardized estimate of the parameter location
Although the _SDEST_ and _SDSE_ variables are created for COSAN models, the values for these two variables are always missing because there are no rules
to carry out the standardization of COSAN models.
Each observation (record) of the OUTMODEL= data set contains a piece of information regarding the model specification. Depending
on the type of the specification indicated by the value of the _TYPE_ variable, the meanings of _NAME_, _VAR1_, and _VAR2_ differ. The following tables summarize the meanings of the _NAME_, _MATNR_ (COSAN models only), _VAR1_, and _VAR2_ variables for each value of the _TYPE_ variable, given the type of the model.
COSAN Models
|
|
Description |
|
|
|
|
|---|---|---|---|---|---|
|
MDLTYPE |
Model type |
COSAN |
|||
|
VAR |
Variable |
Variable name |
Matrix number |
Column location |
|
|
MATRIX |
Matrix |
Matrix name |
Matrix number |
Number of rows |
Number of columns |
|
MODEL |
Model formula |
COV or MEAN |
Matrix number |
Term number |
Location in term |
|
ESTIM |
Parameters |
Parameter name |
Matrix number |
Row number |
Column number |
The value of the _NAME_ variable is COSAN for the _TYPE_=MDLTYPE observation.
The _TYPE_=VAR observations store the information about the column variables in matrices. The _NAME_ variable stores the variable names. The value of _VAR1_ indicates the column location of the variable in the matrix with the matrix number stored in _MATNR_.
The _TYPE_=MATRIX observations store the information about the model matrices. The _NAME_ variable stores the matrix names. The value of _MATNR_ indicates the corresponding matrix number. The values of_VAR1_ and _VAR2_ indicates the numbers of rows and columns, respectively, of the matrix.
The _TYPE_=MODEL observations store the covariance and mean structure formulas. The _NAME_ variable indicates whether the mean (MEAN) or covariance (COV) structure information is stored. The value of _MATNR_ indicates the matrix number in the mean or covariance structure formula. The _VAR1_ variable indicates the term number, and the _VAR2_ variable indicates the location of the matrix in the term.
The _TYPE_=ESTIM observations store the information about the parameters and their estimates. The _NAME_ variable stores the parameter names. The value of _MATNR_ indicates the matrix number. The values of _VAR1_ and _VAR2_ indicate the associated row and column numbers, respectively, of the parameter.
FACTOR Models
|
|
Description |
|
|
|
|---|---|---|---|---|
|
MDLTYPE |
Model type |
Model type |
||
|
FACTVAR |
Variable |
Variable name |
Variable number |
Variable type |
|
LOADING |
Factor loading |
Parameter name |
Manifest variable |
Factor variable |
|
COV |
Covariance |
Parameter name |
First variable |
Second variable |
|
PVAR |
(Partial) variance |
Parameter name |
Variable |
|
|
MEAN |
Mean or intercept |
Parameter name |
Variable |
|
|
ADDCOV |
Added covariance |
Parameter name |
First variable |
Second variable |
|
ADDPVAR |
Added (partial) variance |
Parameter name |
Variable |
|
|
ADDMEAN |
Added mean or intercept |
Parameter name |
Variable |
For factor models, the value of the _NAME_ variable is either EFACTOR (exploratory factor model) or CFACTOR (confirmatory factor model) for the _TYPE_=MDLTYPE observation.
The _TYPE_=FACTVAR observations store the information about the variables in the model. The _NAME_ variable stores the variable names. The value of _VAR1_ indicates the variable number. The value of _VAR2_ indicates the type of the variable: either DEPV for dependent observed variables or INDF for latent factors.
Other observations specify the parameters and their estimates in the model. The _NAME_ values for these observations are the parameter names. Observation with _TYPE_=LOADING, _TYPE_=COV, or _TYPE_=ADDCOV are for parameters that are associated with two variables. The _VAR1_ and _VAR2_ values of these two types of observations indicate the variables involved.
Observations with _TYPE_=PVAR, _TYPE_=MEAN, _TYPE_=ADDPVAR, or _TYPE_=ADDMEAN are for parameters that are associated with a single variable. The value of _VAR1_ indicates the variable involved.
LINEQS Models
|
|
Description |
|
|
|
|---|---|---|---|---|
|
MDLTYPE |
Model type |
LINEQS |
||
|
EQSVAR |
Variable |
Variable name |
Variable number |
Variable type |
|
EQUATION |
Path coefficient |
Parameter |
Outcome variable |
Predictor variable |
|
COV |
Covariance |
Parameter |
First variable |
Second variable |
|
VARIANCE |
Variance |
Parameter |
Variable |
|
|
MEAN |
Mean |
Parameter |
Variable |
|
|
ADDCOV |
Added covariance |
Parameter |
First variable |
Second variable |
|
ADDVARIA |
Added variance |
Parameter |
Variable |
|
|
ADDINTE |
Added intercept |
Parameter |
Variable |
|
|
ADDMEAN |
Added mean |
Parameter |
Variable |
The value of the _NAME_ variable is LINEQS for the _TYPE_=MDLTYPE observation.
The _TYPE_=EQSVAR observations store the information about the variables in the model. The _NAME_ variable stores the variable names. The value of _VAR1_ indicates the variable number. The value of _VAR2_ indicates the type of the variable. There are six types of variables in the LINEQS model:
-
DEPVfor dependent observed variables -
INDVfor independent observed variables -
DEPFfor dependent latent factors -
INDFfor independent latent factors -
INDDfor independent error terms -
INDEfor independent disturbance terms
Other observations specify the parameters and their estimates in the model. The _NAME_ values for these observations are the parameter names. Observation with _TYPE_=EQUATION, _TYPE_=COV, or _TYPE_=ADDCOV are for parameters that are associated with two variables. The _VAR1_ and _VAR2_ values of these two types of observations indicate the variables involved.
Observations with _TYPE_=VARIANCE, _TYPE_=MEAN, _TYPE_=ADDVARIA, _TYPE_=ADDINTE, or _TYPE_=ADDMEAN are for parameters associated with a single variable. The value of _VAR1_ indicates the variable involved.
LISMOD Models
|
|
Description |
|
|
|
|---|---|---|---|---|
|
MDLTYPE |
model type |
LISMOD |
||
|
XVAR |
|
Variable |
Variable number |
|
|
YVAR |
|
Variable |
Variable number |
|
|
ETAVAR |
|
Variable |
Variable number |
|
|
XIVAR |
|
Variable |
Variable number |
|
|
ALPHA |
_ALPHA_ entry |
Parameter |
Row number |
|
|
BETA |
_BETA_ entry |
Parameter |
Row number |
Column number |
|
GAMMA |
_BETA_ entry |
Parameter |
Row number |
Column number |
|
KAPPA |
_KAPPA_ entry |
Parameter |
Row number |
|
|
LAMBDAX |
_LAMBDAX_ entry |
Parameter |
Row number |
Column number |
|
LAMBDAY |
_LAMBDAY_ entry |
Parameter |
Row number |
Column number |
|
NUX |
_NUX_ entry |
Parameter |
Row number |
|
|
NUY |
_NUY_ entry |
Parameter |
Row number |
|
|
PHI |
_PHI_ entry |
Parameter |
Row number |
Column number |
|
PSI |
_PSI_ entry |
Parameter |
Row number |
Column number |
|
THETAX |
_THETAX_ entry |
Parameter |
Row number |
Column number |
|
THETAY |
_THETAY_ entry |
Parameter |
Row number |
Column number |
|
ADDALPHA |
Added _ALPHA_ entry |
Parameter |
Row number |
|
|
ADDKAPPA |
Added _KAPPA_ entry |
Parameter |
Row number |
|
|
ADDNUX |
Added _NUX_ entry |
Parameter |
Row number |
|
|
ADDNUY |
Added _NUY_ entry |
Parameter |
Row number |
|
|
ADDPHI |
Added _PHI_ entry |
Parameter |
Row number |
Column number |
|
ADDPSI |
Added _PSI_ entry |
Parameter |
Row number |
Column number |
|
ADTHETAX |
Added _THETAX_ entry |
Parameter |
Row number |
Column number |
|
ADTHETAY |
Added _THETAY_ entry |
Parameter |
Row number |
Column number |
The value of the _NAME_ variable is LISMOD for the _TYPE_=MDLTYPE observation. Other observations specify either the variables or the parameters in the model.
Observations with _TYPE_ values equal to XVAR, YVAR, ETAVAR, and XIVAR indicate the variables in the respective lists in the model. The _NAME_ variable of these observations stores the names of the variables, and the _VAR1_ variable stores the variable numbers in the respective list. The variable numbers in this data set are not arbitrary—that
is, they define the variable orders in the rows and columns of the LISMOD model matrices. The _VAR2_ variable of these observations is not used.
All other observations in this data set specify the parameters in the model. The _NAME_ values of these observations are the parameter names. The corresponding _VAR1_ and _VAR2_ values of these observations indicate the row and column locations of the parameters in the LISMOD model matrices that are
specified in the _TYPE_ variable. For example, when the value of _TYPE_ is ADDPHI or PHI, the parameter specified is located in the _PHI_ matrix, with its row and column numbers indicated by the _VAR1_ and _VAR2_ values, respectively. Some observations for specifying parameters do not have values in the _VAR2_ variable. This means that the associated LISMOD matrices are vectors so that the column numbers are always 1 for these observations.
MSTRUCT Models
|
|
Description |
|
|
|
|---|---|---|---|---|
|
MDLTYPE |
Model type |
MSTRUCT |
||
|
VAR |
Variable |
Variable |
Variable number |
|
|
COVMAT |
Covariance |
Parameter |
Row number |
Column number |
|
MEANVEC |
Mean |
Parameter |
Row number |
|
|
ADCOVMAT |
Added covariance |
Parameter |
Row number |
Column number |
|
AMEANVEC |
Added mean |
Parameter |
Row number |
The value of the _NAME_ variable is MSTRUCT for the _TYPE_=MDLTYPE observation. Other observations specify either the variables or the parameters in the model.
Observations with _TYPE_ values equal to VAR indicate the variables in the model. The _NAME_ variable of these observations stores the names of the variables, and the _VAR1_ variable stores the variable numbers in the variable list. The variable numbers in this data set are not arbitrary—that is,
they define the variable orders in the rows and columns of the mean and covariance matrices. The _VAR2_ variable of these observations is not used.
All other observations in this data set specify the parameters in the model. The _NAME_ values of these observations are the parameter names. The corresponding _VAR1_ and _VAR2_ values of these observations indicate the row and column locations of the parameters in the mean or covariance matrix, as
specified in the _TYPE_ model. For example, when _TYPE_=COVMAT, the parameter specified is located in the covariance matrix, with its row and column numbers indicated by the _VAR1_ and _VAR2_ values, respectively. For observations with _TYPE_=MEANVEC, the _VAR2_ variable is not used because the column numbers are always 1 for parameters in the mean vector.
PATH Models
|
|
Description |
|
|
|
|---|---|---|---|---|
|
MDLTYPE |
Model type |
PATH |
||
|
PATHVAR |
Variable |
Variable name |
Variable number |
Variable type |
|
LEFT |
Path coefficient |
Parameter |
Outcome variable |
Predictor variable |
|
RIGHT |
Path coefficient |
Parameter |
Predictor variable |
Outcome variable |
|
PCOV |
(Partial) covariance |
Parameter |
First variable |
Second variable |
|
PCOVPATH |
(Partial) covariance path |
Parameter |
First variable |
Second variable |
|
PVAR |
(Partial) variance |
Parameter |
Variable |
|
|
PVARPATH |
(Partial) variance path |
Parameter |
Variable |
Variable |
|
MEAN |
Mean or intercept |
Parameter |
Variable |
|
|
ONEPATH |
Mean or intercept path |
Parameter |
_ONE_ |
Variable |
|
ADDPCOV |
Added (partial) covariance |
Parameter |
First variable |
Second variable |
|
ADDPVAR |
Added (partial) variance |
Parameter |
Variable |
|
|
ADDMEAN |
Added mean |
Parameter |
Variable |
The value of the _NAME_ variable is PATH for the _TYPE_=MDLTYPE observation.
The _TYPE_=PATHVAR observations store the information about the variables in the model. The _NAME_ variable stores the variable names. The value of _VAR1_ indicates the variable number. The value of _VAR2_ indicates the type of the variable. There are four types of variables in the PATH model:
-
DEPVfor dependent observed variables -
INDVfor independent observed variables -
DEPFfor dependent latent factors -
INDFfor independent latent factors
Other observations specify the parameters in the model. The _NAME_ values for these observations are the parameter names. Observation with _TYPE_=LEFT, _TYPE_=RIGHT, _TYPE_=PCOV, or _TYPE_=ADDPCOV are for parameters that are associated with two variables. The _VAR1_ and _VAR2_ values of these two types of observations indicate the variables involved.
Observations with _TYPE_=PVAR, _TYPE_=MEAN, _TYPE_=ADDPVAR, or _TYPE_=ADDMEAN are for parameters that are associated with a single variable. The value of _VAR1_ indicates the variable involved.
RAM Models
|
|
Description |
|
|
|
|---|---|---|---|---|
|
MDLTYPE |
Model type |
RAM |
||
|
RAMVAR |
Variable name |
Variable |
Variable number |
Variable type |
|
_A_ |
|
Parameter |
Row number |
Column number |
|
_P_ |
|
Parameter |
Row number |
Column number |
|
_W_ |
|
Parameter |
Row number |
Column number |
|
ADD_P_ |
Added |
Parameter |
Row number |
Column number |
|
ADD_W_ |
Added |
Parameter |
Row number |
Column number |
The value of the _NAME_ variable is RAM for the _TYPE_=MDLTYPE observation.
For the _TYPE_=RAMVAR observations, the _NAME_ variable stores the variable names, the _VAR1_ variable stores the variable number, and the _VAR2_ variable stores the variable type. There are four types of variables in the PATH model:
-
DEPVfor dependent observed variables -
INDVfor independent observed variables -
DEPFfor dependent latent factors -
INDFfor independent latent factors
Other observations specify the parameters in the model. The _NAME_ variable stores the parameter name. The _TYPE_ variable indicates the associated matrix with the row number indicated in _VAR1_ and column number indicated in _VAR2_.
Reading an OUTMODEL= Data Set As an INMODEL= Data Set in Subsequent Analyses
When the OUTMODEL=
data set is treated as an INMODEL=
data set in subsequent analyses, you need to pay attention to observations with _TYPE_ values prefixed by "ADD", "AD", or "A" (for example, ADDCOV, ADTHETAY, or AMEANVEC). These observations represent default parameter locations that are generated by PROC CALIS in a previous run. Because the
context of the new analyses might be different, these observations for added parameter locations might no longer be suitable
in the new runs. Hence, these observations are not read as input model information. Fortunately, after reading the INMODEL=
specification in the new analyses, CALIS analyzes the new model specification again. It then adds an appropriate set of parameters
in the new context when necessary. If you are certain that the added parameter locations in the INMODEL= data set are applicable,
you can force the input of these observations by using the READADDPARM
option in the PROC CALIS statement. However, you must be very careful about using the READADDPARM
option. The added parameters from the INMODEL= data set might have the same parameter names as those for the generated parameters
in the new run. This might lead to unnecessary constraints in the model.
OUTSTAT= Data Set
The OUTSTAT= data set is similar to the TYPE=COV, TYPE=UCOV, TYPE=CORR, or TYPE=UCORR data set produced by the CORR procedure. The OUTSTAT= data set contains the following variables:
-
the BY variables, if any
-
the _GPNUM_ variable for groups numbers, if used in the analysis
-
two character variables,
_TYPE_and_NAME_ -
the manifest and the latent variables analyzed
The OUTSTAT= data set contains the following information (when available) in the observations:
-
the mean and standard deviation
-
the skewness and kurtosis (if the DATA= data set is a raw data set and the KURTOSIS option is specified)
-
the number of observations
-
if the WEIGHT statement is used, sum of the weights
-
the correlation or covariance matrix to be analyzed
-
the robust covariances, standard deviations, and means for robust estimation
-
the predicted correlation or covariance matrix
-
the standardized or normalized residual correlation or covariance matrix
-
if the model contains latent variables, the predicted covariances between latent and manifest variables and the latent variable (or factor) score regression coefficients (see the PLATCOV option )
In addition, for FACTOR models the OUTSTAT= data set contains:
If effects are analyzed, the OUTSTAT= data set also contains:
-
direct, indirect, and total effects and their standard error estimates
-
standardized direct, indirect, and total effects and their standard error estimates
Each observation in the OUTSTAT=
data set contains some type of statistic as indicated by the _TYPE_ variable. The values of the _TYPE_ variable are shown in the following tables:
Basic Descriptive Statistics
|
Value of |
Contents |
|---|---|
|
ADJCOV |
Adjusted covariances |
|
ADJSTD |
Adjusted standard deviations |
|
CORR |
Correlations |
|
COV |
Covariances |
|
KURTOSIS |
Univariate kurtosis |
|
MEAN |
Means |
|
N |
Sample size |
|
NPARTIAL |
Number of partial variables |
|
PARTCOV |
Covariances after partialling |
|
PARTCORR |
Correlations after partialling |
|
PARTMEAN |
Means after partialling |
|
PARTSTD |
Standard deviations after partialling |
|
ROBCOV |
Robust covariances |
|
ROBMEAN |
Robust means |
|
ROBSTD |
Robust standard deviations |
|
SKEWNESS |
Univariate skewness |
|
STD |
Standard deviations |
|
SUMWGT |
Sum of weights (if the WEIGHT statement is used) |
|
VARDIV |
Variance divisor |
|
VARDIVAJ |
Variance divisor adjustment |
For the _TYPE_=CORR or COV observations, the _NAME_ variable contains the name of the manifest variable that corresponds to each row for the covariance or correlation. For other
observations, _NAME_ is blank.
Predicted Moments and Residuals
|
Value of |
Contents |
|---|---|
|
METHOD= DWLS |
|
|
DWLSPRED |
DWLS predicted moments |
|
DWLSRES |
DWLS raw residuals |
|
DWLSSRES |
DWLS variance standardized residuals |
|
METHOD= GLS |
|
|
GLSASRES |
GLS asymptotically standardized residuals |
|
GLSNRES |
GLS normalized residuals |
|
GLSPRED |
GLS predicted moments |
|
GLSRES |
GLS raw residuals |
|
GLSSRES |
GLS variance standardized residuals |
|
METHOD= ML or FIML |
|
|
MAXASRES |
ML asymptotically standardized residuals |
|
MAXNRES |
ML normalized residuals |
|
MAXPRED |
ML predicted moments |
|
MAXRES |
ML raw residuals |
|
MAXSRES |
ML variance standardized residuals |
|
METHOD= ULS |
|
|
ULSPRED |
ULS predicted moments |
|
ULSRES |
ULS raw residuals |
|
ULSSRES |
ULS variance standardized residuals |
|
METHOD= WLS |
|
|
WLSASRES |
WLS asymptotically standardized residuals |
|
WLSNRES |
WLS normalized residuals |
|
WLSPRED |
WLS predicted moments |
|
WLSRES |
WLS raw residuals |
|
WLSSRES |
WLS variance standardized residuals |
For residuals or predicted moments of means, the _NAME_ variable is a fixed value denoted by _Mean_. For residuals or predicted moments for covariances or correlations, the _NAME_ variable is used for names of variables.
Effects and Latent Variable Scores Regression Coefficients
|
Value of |
Contents |
|---|---|
|
Unstandardized Effects |
|
|
DEFFECT |
Direct effects |
|
DEFF_SE |
Standard error estimates for direct effects |
|
IEFFECT |
Indirect effects |
|
IEFF_SE |
Standard error estimates for indirect effects |
|
TEFFECT |
Total effects |
|
TEFF_SE |
Standard error estimates for total effects |
|
Standardized Effects |
|
|
SDEFF |
Standardized direct effects |
|
SDEFF_SE |
Standard error estimates for standardized direct effects |
|
SIEFF |
Standardized indirect effects |
|
SIEFF_SE |
Standard error estimates for standardized indirect effects |
|
STEFF |
Standardized total effects |
|
STEFF_SE |
Standard error estimates for standardized total effects |
|
Latent Variable Scores Coefficients |
|
|
LSSCORE |
Latent variable (or factor) scores regression coefficients for ULS method |
|
SCORE |
Latent variable (or factor) scores regression coefficients other than ULS method |
For latent variable or factor scores coefficients, the _NAME_ variable contains factor or latent variables in the observations. For other observations, the _NAME_ variable contains manifest or latent variable names.
You can use the latent variable score regression coefficients with PROC SCORE to compute factor scores.
If the analyzed matrix is a covariance rather than a correlation matrix, the _TYPE_=STD observation is not included in the OUTSTAT=
data set. In this case, the standard deviations can be obtained from the diagonal elements of the covariance matrix. Dropping
the _TYPE_=STD observation prevents PROC SCORE from standardizing the observations before computing the factor scores.
Factor Analysis Results
|
Value of |
Contents |
|---|---|
|
ERRVAR |
Error variances |
|
FCOV |
Factor correlations or covariances |
|
LOADINGS |
Unrotated factor loadings |
|
RFCOV |
Rotated factor correlations or covariances |
|
RLOADING |
Rotated factor loadings |
|
ROTMAT |
Rotation matrix |
|
STDERVAR |
Error variances in standardized solutions |
|
STDFCOV |
Standardized factor correlations |
|
STDLOAD |
Standardized factor loadings |
|
STDRFCOV |
Standardized rotated factor correlations or covariances |
|
STDRLOAD |
Standardized rotated factor loadings |
For the _TYPE_=ERRVAR observation, the _NAME_ variable is blank. For all other observations, the _NAME_ variable contains factor names.
OUTWGT= Data Set
You can create an OUTWGT=
data set that is of TYPE=WEIGHT and contains the weight matrix used in generalized, weighted, or diagonally weighted least
squares estimation. The OUTWGT=
data set contains the weight matrix on which the WRIDGE=
and the WPENALTY=
options are applied. However, if you input the inverse of the weight matrix with the INWGT=
and INWGTINV
options (or the INWGT(INV)=
option alone) in the same analysis, the OUTWGT=
data set contains the same elements of the inverse of the weight matrix. For unweighted least squares or maximum likelihood
estimation, no OUTWGT=
data set can be written. The weight matrix used in maximum likelihood estimation is dynamically updated during optimization.
When the ML solution converges, the final weight matrix is the same as the predicted covariance or correlation matrix,
which is included in the OUTSTAT=
data set (observations with _TYPE_ =MAXPRED).
For generalized and diagonally weighted least squares estimation, the weight matrices 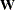 of the OUTWGT=
data set contain all elements
of the OUTWGT=
data set contain all elements 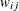 , where the indices i and j correspond to all manifest variables used in the analysis. Let
, where the indices i and j correspond to all manifest variables used in the analysis. Let 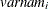 be the name of the ith variable in the analysis. In this case, the OUTWGT=
data set contains n observations with the variables shown in the following table:
be the name of the ith variable in the analysis. In this case, the OUTWGT=
data set contains n observations with the variables shown in the following table:
|
Variable |
Contents |
|---|---|
|
|
WEIGHT (character) |
|
|
Name of variable |
|
|
Weight |
|
|
|
|
|
Weight |
For weighted least squares estimation, the weight matrix 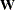 of the OUTWGT=
data set contains only the nonredundant elements
of the OUTWGT=
data set contains only the nonredundant elements 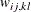 . In this case, the OUTWGT=
data set contains
. In this case, the OUTWGT=
data set contains 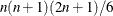 observations with the variables shown in the following table:
observations with the variables shown in the following table:
|
Variable |
Contents |
|---|---|
|
|
WEIGHT (character) |
|
|
Name of variable |
|
|
Name of variable |
|
|
Name of variable |
|
|
Weight |
|
|
|
|
|
Weight |
Symmetric redundant elements are set to missing values.
OUTFIT= Data Set
You can create an OUTFIT= data set that is of TYPE=CALISFIT and that contains the values of the fit indices of your analysis. If you use two estimation methods such as LSML or LSWLS, the fit indices are for the second analysis. An OUTFIT= data set contains the following variables:
-
a character variable
_TYPE_for the types of fit indices -
a numerical variable
IndexCodefor the codes of the fit indices -
a character variable
FitIndexfor the names of the fit indices -
a numerical variable
FitValuefor the numerical values of the fit indices -
a character variable
PrintCharfor the character-formatted fit index values.
The possible values of _TYPE_ are:
ModelInfo:-
basic modeling statistics and information
Absolute:-
stand-alone fit indices
Parsimony:-
fit indices that take model parsimony into account
Incremental:-
fit indices that are based on comparison with a baseline model
Possible Values of FitIndex When _TYPE_=ModelInfo
|
Value of |
Description |
|---|---|
|
Number of Observations |
Number of observations used in the analysis |
|
Number of Complete Observations |
Number of complete observations (METHOD=FIML) |
|
Number of Incomplete Observations |
Number of incomplete observations (METHOD=FIML) |
|
Number of Variables |
Number of variables |
|
Number of Moments |
Number of mean or covariance elements |
|
Number of Parameters |
Number of parameters |
|
Number of Active Constraints |
Number of active constraints in the solution |
|
Saturated Model Estimation |
Estimation status of the saturated model (METHOD=FIML) |
|
Saturated Model Function Value |
Saturated model function value (METHOD=FIML) |
|
Saturated Model -2 Log-Likelihood |
Saturated model –2 log-likelihood function value (METHOD=FIML) |
|
Baseline Model Estimation |
Estimation status of the baseline model (METHOD=FIML) |
|
Baseline Model Function Value |
Baseline model function value |
|
Baseline Model -2 Log-Likelihood |
Baseline model –2 log-likelihood function value (METHOD=FIML) |
|
Baseline Model Chi-Square |
Baseline model chi-square value |
|
Baseline Model Chi-Square DF |
Baseline model chi-square degrees of freedom |
|
Baseline Model DF |
Baseline model degrees of freedom (METHOD=ULS or METHOD=DWLS) |
|
Pr > Baseline Model Chi-Square |
p-value of the baseline model chi-square |
|
SB-Scaled Base Model Chi-Square |
Satorra-Bentler scaled chi-square for the baseline model |
|
Pr > SB-Scaled Base Model Chi-Square |
p-value of the Satorra-Bentler scaled chi-square for the baseline model |
Possible Values of FitIndex When _TYPE_=Absolute
|
Value of |
Description |
|---|---|
|
Fit Function |
Fit function value |
|
-2 Log-Likelihood |
–2 log-likelihood function value for the model (METHOD=FIML) |
|
Chi-Square |
Model chi-square value |
|
Chi-Square DF |
Degrees of freedom for the model chi-square test |
|
Model DF |
Degrees of freedom for model (METHOD=ULS or METHOD=DWLS) |
|
Pr > Chi-Square |
Probability of obtaining a larger chi-square than the observed value |
|
SB-Scaled Model Chi-Square |
Satorra-Bentler scaled chi-square for the model |
|
Pr > SB-Scaled Model Chi-Square |
Probability of obtaining a larger chi-square than the observed Satorra-Bentler scaled chi-square value |
|
Elliptic Corrected Chi-Square |
Elliptic-corrected chi-square value |
|
Pr > Elliptic Corr. Chi-Square |
Probability of obtaining a larger elliptic-corrected chi-square value |
|
Z-test of Wilson and Hilferty |
Z-test of Wilson and Hilferty |
|
Hoelter Critical N |
N value that makes a significant chi-square when multiplied to the fit function value |
|
Root Mean Square Residual (RMR) |
Root mean square residual |
|
Standardized RMR (SRMR) |
Standardized root mean square residual |
|
Goodness of Fit Index (GFI) |
Jöreskog and Sörbom goodness-of-fit index |
Possible Values of FitIndex When _TYPE_=Parsimony
|
Value of |
Description |
|---|---|
|
Adjusted GFI (AGFI) |
Goodness-of-fit index adjusted for the degrees of freedom of the model |
|
Parsimonious GFI |
Mulaik et al. (1989) modification of the GFI |
|
RMSEA Estimate |
Steiger and Lind (1980) root mean square error of approximation |
|
RMSEA Lower r% Confidence Limit |
Lower r% |
|
RMSEA Upper r% Confidence Limit |
Upper r% |
|
Probability of Close Fit |
Browne and Cudeck (1993) test of close fit |
|
ECVI Estimate |
Expected cross-validation index |
|
ECVI Lower r% Confidence Limit |
Lower r% |
|
ECVI Upper r% Confidence Limit |
Upper r% |
|
Akaike Information Criterion |
Akaike information criterion |
|
Bozdogan CAIC |
Bozdogan (1987) consistent AIC |
|
Schwarz Bayesian Criterion |
Schwarz (1978) Bayesian criterion |
|
McDonald Centrality |
McDonald and Marsh (1988) measure of centrality |
1. The value of r is one minus the ALPHARMS= value. By default, r=90. 2. The value of r is one minus the ALPHAECV= value. By default, r=90.
Possible Values of FitIndex When _TYPE_=Incremental
|
Value of |
Description |
|---|---|
|
Bentler Comparative Fit Index |
Bentler (1985) comparative fit index |
|
Bentler-Bonett NFI |
Bentler and Bonett (1980) normed fit index |
|
Bentler-Bonett Non-normed Index |
Bentler and Bonett (1980) nonnormed fit index |
|
Bollen Normed Index Rho1 |
Bollen normed |
|
Bollen Non-normed Index Delta2 |
Bollen nonnormed |
|
James et al. Parsimonious NFI |
James, Mulaik, and Brett (1982) parsimonious normed fit index |