The CALIS Procedure
-
Overview

-
Getting Started

-
Syntax
 Classes of Statements in PROC CALISSingle-Group Analysis SyntaxMultiple-Group Multiple-Model Analysis SyntaxPROC CALIS StatementBOUNDS StatementBY StatementCOSAN StatementCOV StatementDETERM StatementEFFPART StatementFACTOR StatementFITINDEX StatementFREQ StatementGROUP StatementLINCON StatementLINEQS StatementLISMOD StatementLMTESTS StatementMATRIX StatementMEAN StatementMODEL StatementMSTRUCT StatementNLINCON StatementNLOPTIONS StatementOUTFILES StatementPARAMETERS StatementPARTIAL StatementPATH StatementPATHDIAGRAM StatementPCOV StatementPVAR StatementRAM StatementREFMODEL StatementRENAMEPARM StatementSAS Programming StatementsSIMTESTS StatementSTD StatementSTRUCTEQ StatementTESTFUNC StatementVAR StatementVARIANCE StatementVARNAMES StatementWEIGHT Statement
Classes of Statements in PROC CALISSingle-Group Analysis SyntaxMultiple-Group Multiple-Model Analysis SyntaxPROC CALIS StatementBOUNDS StatementBY StatementCOSAN StatementCOV StatementDETERM StatementEFFPART StatementFACTOR StatementFITINDEX StatementFREQ StatementGROUP StatementLINCON StatementLINEQS StatementLISMOD StatementLMTESTS StatementMATRIX StatementMEAN StatementMODEL StatementMSTRUCT StatementNLINCON StatementNLOPTIONS StatementOUTFILES StatementPARAMETERS StatementPARTIAL StatementPATH StatementPATHDIAGRAM StatementPCOV StatementPVAR StatementRAM StatementREFMODEL StatementRENAMEPARM StatementSAS Programming StatementsSIMTESTS StatementSTD StatementSTRUCTEQ StatementTESTFUNC StatementVAR StatementVARIANCE StatementVARNAMES StatementWEIGHT Statement -
Details
 Input Data SetsOutput Data SetsDefault Analysis Type and Default ParameterizationThe COSAN ModelThe FACTOR ModelThe LINEQS ModelThe LISMOD Model and SubmodelsThe MSTRUCT ModelThe PATH ModelThe RAM ModelNaming Variables and ParametersSetting Constraints on ParametersAutomatic Variable SelectionPath Diagrams: Layout Algorithms, Default Settings, and CustomizationEstimation CriteriaRelationships among Estimation CriteriaGradient, Hessian, Information Matrix, and Approximate Standard ErrorsCounting the Degrees of FreedomAssessment of FitCase-Level Residuals, Outliers, Leverage Observations, and Residual DiagnosticsLatent Variable ScoresTotal, Direct, and Indirect EffectsStandardized SolutionsModification IndicesMissing Values and the Analysis of Missing PatternsMeasures of Multivariate KurtosisInitial EstimatesUse of Optimization TechniquesComputational ProblemsDisplayed OutputODS Table NamesODS Graphics
Input Data SetsOutput Data SetsDefault Analysis Type and Default ParameterizationThe COSAN ModelThe FACTOR ModelThe LINEQS ModelThe LISMOD Model and SubmodelsThe MSTRUCT ModelThe PATH ModelThe RAM ModelNaming Variables and ParametersSetting Constraints on ParametersAutomatic Variable SelectionPath Diagrams: Layout Algorithms, Default Settings, and CustomizationEstimation CriteriaRelationships among Estimation CriteriaGradient, Hessian, Information Matrix, and Approximate Standard ErrorsCounting the Degrees of FreedomAssessment of FitCase-Level Residuals, Outliers, Leverage Observations, and Residual DiagnosticsLatent Variable ScoresTotal, Direct, and Indirect EffectsStandardized SolutionsModification IndicesMissing Values and the Analysis of Missing PatternsMeasures of Multivariate KurtosisInitial EstimatesUse of Optimization TechniquesComputational ProblemsDisplayed OutputODS Table NamesODS Graphics -
Examples
 Estimating Covariances and CorrelationsEstimating Covariances and Means SimultaneouslyTesting Uncorrelatedness of VariablesTesting Covariance PatternsTesting Some Standard Covariance Pattern HypothesesLinear Regression ModelMultivariate Regression ModelsMeasurement Error ModelsTesting Specific Measurement Error ModelsMeasurement Error Models with Multiple PredictorsMeasurement Error Models Specified As Linear EquationsConfirmatory Factor ModelsConfirmatory Factor Models: Some VariationsResidual Diagnostics and Robust EstimationThe Full Information Maximum Likelihood MethodComparing the ML and FIML EstimationPath Analysis: Stability of AlienationSimultaneous Equations with Mean Structures and Reciprocal PathsFitting Direct Covariance StructuresConfirmatory Factor Analysis: Cognitive AbilitiesTesting Equality of Two Covariance Matrices Using a Multiple-Group AnalysisTesting Equality of Covariance and Mean Matrices between Independent GroupsIllustrating Various General Modeling LanguagesTesting Competing Path Models for the Career Aspiration DataFitting a Latent Growth Curve ModelHigher-Order and Hierarchical Factor ModelsLinear Relations among Factor LoadingsMultiple-Group Model for Purchasing BehaviorFitting the RAM and EQS Models by the COSAN Modeling LanguageSecond-Order Confirmatory Factor AnalysisLinear Relations among Factor Loadings: COSAN Model SpecificationOrdinal Relations among Factor LoadingsLongitudinal Factor Analysis
Estimating Covariances and CorrelationsEstimating Covariances and Means SimultaneouslyTesting Uncorrelatedness of VariablesTesting Covariance PatternsTesting Some Standard Covariance Pattern HypothesesLinear Regression ModelMultivariate Regression ModelsMeasurement Error ModelsTesting Specific Measurement Error ModelsMeasurement Error Models with Multiple PredictorsMeasurement Error Models Specified As Linear EquationsConfirmatory Factor ModelsConfirmatory Factor Models: Some VariationsResidual Diagnostics and Robust EstimationThe Full Information Maximum Likelihood MethodComparing the ML and FIML EstimationPath Analysis: Stability of AlienationSimultaneous Equations with Mean Structures and Reciprocal PathsFitting Direct Covariance StructuresConfirmatory Factor Analysis: Cognitive AbilitiesTesting Equality of Two Covariance Matrices Using a Multiple-Group AnalysisTesting Equality of Covariance and Mean Matrices between Independent GroupsIllustrating Various General Modeling LanguagesTesting Competing Path Models for the Career Aspiration DataFitting a Latent Growth Curve ModelHigher-Order and Hierarchical Factor ModelsLinear Relations among Factor LoadingsMultiple-Group Model for Purchasing BehaviorFitting the RAM and EQS Models by the COSAN Modeling LanguageSecond-Order Confirmatory Factor AnalysisLinear Relations among Factor Loadings: COSAN Model SpecificationOrdinal Relations among Factor LoadingsLongitudinal Factor Analysis - References
Example 29.19 Fitting Direct Covariance Structures
In the section Direct Covariance Structures Analysis, the MSTRUCT modeling language is used to specify a model with direct covariance structures. In the model, four variables from the data set of Wheaton et al. (1977) are used. The analysis is carried out in this example to investigate the tenability of the hypothesized covariance structures.
The four variables used are: Anomie67, Powerless67, Anomie71, and Powerless71. The hypothesized covariance matrix is structured as:
![\[ \bSigma = \left( \begin{array}{cccc} \phi _1 & \theta _1 & \theta _2 & \theta _1 \\ \theta _1 & \phi _2 & \theta _ l & \theta _3 \\ \theta _2 & \theta _1 & \phi _1 & \theta _1 \\ \theta _1 & \theta _3 & \theta _1 & \phi _2 \\ \end{array} \right) \quad \]](images/statug_calis0967.png)
where:
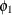 :
:-
variance of anomie
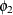 :
:-
variance of powerlessness
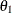 :
:-
covariance between anomie and powerlessness
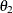 :
:-
covariance between anomie measures
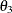 :
:-
covariance between powerlessness measures
In this example, you hypothesize the covariance structures directly, as opposed to those models with implied covariance structures
from path models (see Example 29.17), structural equations (see Example 29.18), or other types of models. The basic assumption of the direct covariance structures in this example is that Anomie and Powerless were invariant over the measurement periods employed. This implies that the time of measurement did not change the variances
and covariances of the measures. Therefore, both Anomie67 and Anomie71 have the same variance parameter 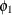 , and both
, and both Powerless67 and Powerless71 have the same variance parameter 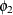 . These two parameters,
. These two parameters, 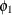 and
and 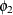 , are hypothesized on the diagonal of the covariance matrix
, are hypothesized on the diagonal of the covariance matrix 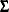 . In the same structured covariance matrix,
. In the same structured covariance matrix, 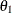 represents the covariance between
represents the covariance between Anomie and Powerless, without regard to the time of measurement. The 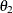 parameter represents the covariance between the
parameter represents the covariance between the Anomie measures, or the reliability of the Anomie measure. Similarly, the 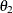 parameter represents the covariance between the
parameter represents the covariance between the Powerless measures, or the reliability of the Anomie measure.
As explained in the section Direct Covariance Structures Analysis, you can use the MSTRUCT modeling language to specify the hypothesized covariance structures directly, as shown in the following statements:
proc calis nobs=932 data=Wheaton psummary;
fitindex on(only)=[chisq df probchi] outfit=savefit;
mstruct
var = Anomie67 Powerless67 Anomie71 Powerless71;
matrix _COV_ [1,1] = phi1,
[2,2] = phi2,
[3,3] = phi1,
[4,4] = phi2,
[2,1] = theta1,
[3,1] = theta2,
[3,2] = theta1,
[4,1] = theta1,
[4,2] = theta3,
[4,3] = theta1;
run;
In the MSTRUCT statement you specify the variables in the VAR= list. The order of variables in this VAR= list is assumed to be the same as that in the row and column of the hypothesized covariance matrix. Next, in the MATRIX statement you specify parameters as entries in the hypothesized covariance matrix _COV_. Only the lower diagonal elements need to be specified because covariance matrices, by nature, are symmetric. Redundant specification of the upper triangular elements are unnecessary as PROC CALIS has the information accounted for. You can also set initial estimates by putting parenthesized numbers after the parameter names. But in this example you let PROC CALIS determine all the initial estimates.
In the PROC CALIS statement, the PSUMMARY option is used. As a global display option , this option suppresses a lot of displayed output and requests only the fit summary table be printed. This way you can eliminate quite a lot of displayed output that is not of your primary interest. In this example, the specification of the covariance structures is straightforward, and you do not need any output regarding the initial estimation or standardized solution. Suppose that you are not even concerned with the estimates of the parameters because you are not yet sure if this model is good enough for the data. All you want to know at this stage is whether the hypothesized covariance structures fit the data well. Therefore, the PSUMMARY option would serve your purpose well in this example.
In fact, even the fit summary table can be trimmed down quite a bit if you only want to look at certain specific fit indices.
In the FITINDEX
statement of this example, the ON(ONLY)= option turns on the printing of the model fit chi-square, its df, and p-value only. This does not mean that you must lose the information of all other fit indices. In addition to the printed output,
you can save all fit indices in an output data set. To this end, you can use the OUTFIT=
option in the FITINDEX
statement. In this example, you save the results of all fit indices in a SAS data set called savefit.
Output 29.19.1 shows the entire printed output.
Output 29.19.1: Testing Direct Covariance Structures
The displayed output is very concise. It contains only a fit summary table with three statistics. The p-value for the model fit chi-square test indicates that the hypothesized structures should be rejected at 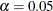 . Therefore, this rather restrictive direct covariance structure model does not fit the data well. A less restrictive covariance
structure model is needed to explain the variances and covariances.
. Therefore, this rather restrictive direct covariance structure model does not fit the data well. A less restrictive covariance
structure model is needed to explain the variances and covariances.
All fit indices are saved in the savefit data set. To view it, you can use the following statement:
proc print data=savefit; run;
Output 29.19.2 shows all indices, their types and values of all fit indices and information.
Output 29.19.2: Saved Fit Indices
| Analysis of Direct Covariance Structures |
| Testing Model by the MSTRUCT Language |
| Obs | _TYPE_ | IndexCode | FitIndex | FitValue | PrintChar |
|---|---|---|---|---|---|
| 1 | ModelInfo | 101 | Number of Observations | 932.00 | 932 |
| 2 | ModelInfo | 103 | Number of Variables | 4.00 | 4 |
| 3 | ModelInfo | 104 | Number of Moments | 10.00 | 10 |
| 4 | ModelInfo | 105 | Number of Parameters | 5.00 | 5 |
| 5 | ModelInfo | 106 | Number of Active Constraints | 0.00 | 0 |
| 6 | ModelInfo | 111 | Baseline Model Function Value | 1.68 | 1.6799 |
| 7 | ModelInfo | 113 | Baseline Model Chi-Square | 1563.94 | 1563.9442 |
| 8 | ModelInfo | 114 | Baseline Model Chi-Square DF | 6.00 | 6 |
| 9 | ModelInfo | 115 | Pr > Baseline Model Chi-Square | 0.00 | <.0001 |
| 10 | Absolute | 201 | Fit Function | 0.24 | 0.2380 |
| 11 | Absolute | 203 | Chi-Square | 221.58 | 221.5798 |
| 12 | Absolute | 204 | Chi-Square DF | 5.00 | 5 |
| 13 | Absolute | 205 | Pr > Chi-Square | 0.00 | <.0001 |
| 14 | Absolute | 211 | Z-Test of Wilson & Hilferty | 12.25 | 12.2533 |
| 15 | Absolute | 212 | Hoelter Critical N | 47.00 | 47 |
| 16 | Absolute | 213 | Root Mean Square Residual (RMR) | 0.76 | 0.7649 |
| 17 | Absolute | 214 | Standardized RMR (SRMR) | 0.07 | 0.0701 |
| 18 | Absolute | 215 | Goodness of Fit Index (GFI) | 0.90 | 0.9036 |
| 19 | Parsimony | 301 | Adjusted GFI (AGFI) | 0.81 | 0.8071 |
| 20 | Parsimony | 302 | Parsimonious GFI | 0.75 | 0.7530 |
| 21 | Parsimony | 303 | RMSEA Estimate | 0.22 | 0.2157 |
| 22 | Parsimony | 304 | RMSEA Lower 90% Confidence Limit | 0.19 | 0.1920 |
| 23 | Parsimony | 305 | RMSEA Upper 90% Confidence Limit | 0.24 | 0.2404 |
| 24 | Parsimony | 306 | Probability of Close Fit | 0.00 | <.0001 |
| 25 | Parsimony | 307 | ECVI Estimate | 0.25 | 0.2488 |
| 26 | Parsimony | 308 | ECVI Lower 90% Confidence Limit | 0.20 | 0.2003 |
| 27 | Parsimony | 309 | ECVI Upper 90% Confidence Limit | 0.31 | 0.3053 |
| 28 | Parsimony | 310 | Akaike Information Criterion | 231.58 | 231.5798 |
| 29 | Parsimony | 311 | Bozdogan CAIC | 260.77 | 260.7665 |
| 30 | Parsimony | 312 | Schwarz Bayesian Criterion | 255.77 | 255.7665 |
| 31 | Parsimony | 313 | McDonald Centrality | 0.89 | 0.8903 |
| 32 | Incremental | 401 | Bentler Comparative Fit Index | 0.86 | 0.8610 |
| 33 | Incremental | 403 | Bentler-Bonett NFI | 0.86 | 0.8583 |
| 34 | Incremental | 402 | Bentler-Bonett Non-normed Index | 0.83 | 0.8332 |
| 35 | Incremental | 405 | Bollen Normed Index Rho1 | 0.83 | 0.8300 |
| 36 | Incremental | 406 | Bollen Non-normed Index Delta2 | 0.86 | 0.8611 |
| 37 | Incremental | 404 | James et al. Parsimonious NFI | 0.72 | 0.7153 |
The results of various fit indices from this output data set confirm that the hypothesized model does not fit the data well.
As an aside, it is noted with some shorthand notation, the specification of the MSTRUCT model parameters that use the MATRIX statements can be made a little more precise for the current example. This is shown as follows:
proc calis nobs=932 data=Wheaton psummary;
mstruct
var = Anomie67 Powerless67 Anomie71 Powerless71;
matrix _COV_ [1,1] = phi1 phi2 phi1 phi2,
[2, ] = theta1,
[3, ] = theta2 theta1,
[4, ] = theta1 theta3 theta1;
fitindex on(only)=[chisq df probchi] outfit=savefit;
run;
In the first entry of the MATRIX
statement, the notation [1,1] represents that the parameter list specified after the equal sign starts with the [1,1] element
of the _COV_ matrix and proceeds down the diagonal. In the next three entries, the notations [2,], [3,], and [4,] represent that parameter
lists start with the first elements of the second, third, and fourth rows, respectively, and proceed to the next (right) elements
on the same rows. See the syntax of the
MATRIX statement
for more details about this kind of shorthand notation.
This example shows how you can use the MSTRUCT modeling language to test specific covariance patterns. You need to define the parameters of the covariance patterns explicitly by the MATRIX statements. See Example 29.4 and Example 29.21 for more applications.
However, some commonly-used covariance and mean patterns are built into PROC CALIS. For these covariance and mean patterns, you can simply use the COVPATTERN= and the MEANPATTERN= options without the need to specify the parameters in the MATRIX statements. See the COVPATTERN= and the MEANPATTERN= options for the supported covariance and mean patterns. See Example 29.5 and Example 29.22 for applications.