The CALIS Procedure
-
Overview

-
Getting Started

-
Syntax
 Classes of Statements in PROC CALISSingle-Group Analysis SyntaxMultiple-Group Multiple-Model Analysis SyntaxPROC CALIS StatementBOUNDS StatementBY StatementCOSAN StatementCOV StatementDETERM StatementEFFPART StatementFACTOR StatementFITINDEX StatementFREQ StatementGROUP StatementLINCON StatementLINEQS StatementLISMOD StatementLMTESTS StatementMATRIX StatementMEAN StatementMODEL StatementMSTRUCT StatementNLINCON StatementNLOPTIONS StatementOUTFILES StatementPARAMETERS StatementPARTIAL StatementPATH StatementPATHDIAGRAM StatementPCOV StatementPVAR StatementRAM StatementREFMODEL StatementRENAMEPARM StatementSAS Programming StatementsSIMTESTS StatementSTD StatementSTRUCTEQ StatementTESTFUNC StatementVAR StatementVARIANCE StatementVARNAMES StatementWEIGHT Statement
Classes of Statements in PROC CALISSingle-Group Analysis SyntaxMultiple-Group Multiple-Model Analysis SyntaxPROC CALIS StatementBOUNDS StatementBY StatementCOSAN StatementCOV StatementDETERM StatementEFFPART StatementFACTOR StatementFITINDEX StatementFREQ StatementGROUP StatementLINCON StatementLINEQS StatementLISMOD StatementLMTESTS StatementMATRIX StatementMEAN StatementMODEL StatementMSTRUCT StatementNLINCON StatementNLOPTIONS StatementOUTFILES StatementPARAMETERS StatementPARTIAL StatementPATH StatementPATHDIAGRAM StatementPCOV StatementPVAR StatementRAM StatementREFMODEL StatementRENAMEPARM StatementSAS Programming StatementsSIMTESTS StatementSTD StatementSTRUCTEQ StatementTESTFUNC StatementVAR StatementVARIANCE StatementVARNAMES StatementWEIGHT Statement -
Details
 Input Data SetsOutput Data SetsDefault Analysis Type and Default ParameterizationThe COSAN ModelThe FACTOR ModelThe LINEQS ModelThe LISMOD Model and SubmodelsThe MSTRUCT ModelThe PATH ModelThe RAM ModelNaming Variables and ParametersSetting Constraints on ParametersAutomatic Variable SelectionPath Diagrams: Layout Algorithms, Default Settings, and CustomizationEstimation CriteriaRelationships among Estimation CriteriaGradient, Hessian, Information Matrix, and Approximate Standard ErrorsCounting the Degrees of FreedomAssessment of FitCase-Level Residuals, Outliers, Leverage Observations, and Residual DiagnosticsLatent Variable ScoresTotal, Direct, and Indirect EffectsStandardized SolutionsModification IndicesMissing Values and the Analysis of Missing PatternsMeasures of Multivariate KurtosisInitial EstimatesUse of Optimization TechniquesComputational ProblemsDisplayed OutputODS Table NamesODS Graphics
Input Data SetsOutput Data SetsDefault Analysis Type and Default ParameterizationThe COSAN ModelThe FACTOR ModelThe LINEQS ModelThe LISMOD Model and SubmodelsThe MSTRUCT ModelThe PATH ModelThe RAM ModelNaming Variables and ParametersSetting Constraints on ParametersAutomatic Variable SelectionPath Diagrams: Layout Algorithms, Default Settings, and CustomizationEstimation CriteriaRelationships among Estimation CriteriaGradient, Hessian, Information Matrix, and Approximate Standard ErrorsCounting the Degrees of FreedomAssessment of FitCase-Level Residuals, Outliers, Leverage Observations, and Residual DiagnosticsLatent Variable ScoresTotal, Direct, and Indirect EffectsStandardized SolutionsModification IndicesMissing Values and the Analysis of Missing PatternsMeasures of Multivariate KurtosisInitial EstimatesUse of Optimization TechniquesComputational ProblemsDisplayed OutputODS Table NamesODS Graphics -
Examples
 Estimating Covariances and CorrelationsEstimating Covariances and Means SimultaneouslyTesting Uncorrelatedness of VariablesTesting Covariance PatternsTesting Some Standard Covariance Pattern HypothesesLinear Regression ModelMultivariate Regression ModelsMeasurement Error ModelsTesting Specific Measurement Error ModelsMeasurement Error Models with Multiple PredictorsMeasurement Error Models Specified As Linear EquationsConfirmatory Factor ModelsConfirmatory Factor Models: Some VariationsResidual Diagnostics and Robust EstimationThe Full Information Maximum Likelihood MethodComparing the ML and FIML EstimationPath Analysis: Stability of AlienationSimultaneous Equations with Mean Structures and Reciprocal PathsFitting Direct Covariance StructuresConfirmatory Factor Analysis: Cognitive AbilitiesTesting Equality of Two Covariance Matrices Using a Multiple-Group AnalysisTesting Equality of Covariance and Mean Matrices between Independent GroupsIllustrating Various General Modeling LanguagesTesting Competing Path Models for the Career Aspiration DataFitting a Latent Growth Curve ModelHigher-Order and Hierarchical Factor ModelsLinear Relations among Factor LoadingsMultiple-Group Model for Purchasing BehaviorFitting the RAM and EQS Models by the COSAN Modeling LanguageSecond-Order Confirmatory Factor AnalysisLinear Relations among Factor Loadings: COSAN Model SpecificationOrdinal Relations among Factor LoadingsLongitudinal Factor Analysis
Estimating Covariances and CorrelationsEstimating Covariances and Means SimultaneouslyTesting Uncorrelatedness of VariablesTesting Covariance PatternsTesting Some Standard Covariance Pattern HypothesesLinear Regression ModelMultivariate Regression ModelsMeasurement Error ModelsTesting Specific Measurement Error ModelsMeasurement Error Models with Multiple PredictorsMeasurement Error Models Specified As Linear EquationsConfirmatory Factor ModelsConfirmatory Factor Models: Some VariationsResidual Diagnostics and Robust EstimationThe Full Information Maximum Likelihood MethodComparing the ML and FIML EstimationPath Analysis: Stability of AlienationSimultaneous Equations with Mean Structures and Reciprocal PathsFitting Direct Covariance StructuresConfirmatory Factor Analysis: Cognitive AbilitiesTesting Equality of Two Covariance Matrices Using a Multiple-Group AnalysisTesting Equality of Covariance and Mean Matrices between Independent GroupsIllustrating Various General Modeling LanguagesTesting Competing Path Models for the Career Aspiration DataFitting a Latent Growth Curve ModelHigher-Order and Hierarchical Factor ModelsLinear Relations among Factor LoadingsMultiple-Group Model for Purchasing BehaviorFitting the RAM and EQS Models by the COSAN Modeling LanguageSecond-Order Confirmatory Factor AnalysisLinear Relations among Factor Loadings: COSAN Model SpecificationOrdinal Relations among Factor LoadingsLongitudinal Factor Analysis - References
Example 29.21 Testing Equality of Two Covariance Matrices Using a Multiple-Group Analysis
You can use PROC CALIS to do multiple-group or multiple-sample analysis. The groups in the analysis must be independent. In this example, a relatively simple multiple-group analysis is carried out. The covariance matrices of two independent groups are tested for equality. Hence, individual covariance matrices are actually not structured. Rather, they are constrained to be the same under the null hypothesis. That is, you want to test the following null hypothesis:
![\[ H_0: \bSigma _1 = \bSigma _2 \]](images/statug_calis0968.png)
where 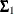 and
and 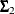 represent the population covariance matrices of the two independent groups in question.
represent the population covariance matrices of the two independent groups in question.
In PROC CALIS, you can use two different approaches to test the equality of covariance matrices. The first approach is to define an MSTRUCT model explicitly and to fit this model to the independent groups. The second approach is to use the COVPATTERN= option to invoke the required covariance structure model for the independent groups. Some standard covariance structures or patterns with the MSTRUCT modeling language are built into PROC CALIS internally. With appropriate keywords for the COVPATTERN= option, you can invoke the target built-in covariance patterns without defining the MSTRUCT model explicitly. This example considers these two approaches successively.
This example is concerned with a reaction time experiment that was conducted on two groups of individuals. One group (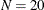 ) was considered to be an expert group with prior training related to the tasks of the experiment. Another group (
) was considered to be an expert group with prior training related to the tasks of the experiment. Another group (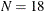 ) was a control group without prior training. Three tasks of dexterity were administered to all individuals. These tasks differed
by their required complexity levels of body skills. They were labeled as high, medium, and low complexities.
) was a control group without prior training. Three tasks of dexterity were administered to all individuals. These tasks differed
by their required complexity levels of body skills. They were labeled as high, medium, and low complexities.
Apparently, the differential performance of the two groups under different task complexities was the primary research objective.
In this example, however, you are interested in testing whether the groups have the same covariance matrix for the tasks.
Equality of covariance matrices might be an essential assumption in some statistical tests for comparing group means. In this
example, the sample covariance matrices for the two groups are stored in the data sets Expert and Novice, as shown in the following:
data expert(type=cov); input _type_ $ _name_ $ high medium low; datalines; COV high 5.88 . . COV medium 2.88 7.16 . COV low 3.12 4.44 8.14 ; data novice(type=cov); input _type_ $ _name_ $ high medium low; datalines; COV high 6.42 . . COV medium 1.24 8.25 . COV low 4.26 2.75 7.99 ;
These data sets are read into the analysis through the GROUP statements in the following PROC CALIS specification:
proc calis;
group 1 / data=expert nobs=20 label="Expert";
group 2 / data=novice nobs=18 label="Novice";
model 1 / groups=1,2;
mstruct
var=high medium low;
fitindex NoIndexType On(only)=[chisq df probchi]
chicorrect=eqcovmat;
ods select ModelingInfo MSTRUCTVariables MSTRUCTCovInit Fit;
run;
The first GROUP
statement defines group 1 for the expert group. The second GROUP
statement defines group 2 for the novice group. You use the NOBS=
option in both statements to provide the number of observations of these groups. You use the LABEL= option in these statements
to provide meaningful group labels.
The MODEL
statement defines MODEL 1. In the analysis, this model fits to both groups 1 and 2, as indicated by the GROUPS= option of the statement. This is done
to test the null hypothesis of equality of covariance matrices in the two groups. An MSTRUCT
model for MODEL 1 is defined immediately afterward. Three variables, high, medium, and low, are specified in the VAR= option of the MSTRUCT
statement.
Without further specification about the MSTRUCT model, PROC CALIS assumes all non redundant elements in the covariance matrix are free parameters. This is what is required under the null hypothesis of the equality of covariance matrices in the two groups—the groups have the same covariance matrix, but the covariance matrix itself is unconstrained. Your model under the null hypothesis is now well-defined and ready to run. In addition, you use FITINDEX and ODS SELECT statements to customize or fine tune the analysis.
By using the options in the FITINDEX statement, you can customize the fit summary table and control some analytic options. In the current example, you use the NOINDEXTYPE option to suppress the printing of the index types in the fit summary table. Then, you use the ON(ONLY)= option to specify the fit indices printed in the fit summary table. In this example, you request only the model fit chi-square statistic, degrees of freedom, and the probability value of the chi-square be printed. Finally, you use the CHICORRECT= EQCOVMAT option to request a chi-square correction for the test of equality of covariance matrices. This correction is due to Box (1949) and is implemented in PROC CALIS as a built-in chi-square correction option.
In addition, because you are not interested in all displayed output for the current hypothesized model, you use the ODS SELECT statement to display only those output (or ODS tables) of interest. In this example, you request only the modeling information, the variables involved, the initial covariance matrix specification, and the fit summary table be printed. All output in PROC CALIS are named as an ODS table. To locate a particular output in PROC CALIS, you must know the corresponding ODS table name. See the section ODS Table Names for a listing of ODS tables produced by PROC CALIS.
Output 29.21.1 displays some information regarding the basic model setup.
Output 29.21.1: Modeling Information and Initial Specification
The modeling information table summarizes some basic information about the two groups. Both of them are fitted by Model 1.
The next table shows the variables involved: high, medium, and low. The order of variables in this table is the same as that of the row and column variables of the covariance model matrix,
which is shown next in Output 29.21.1. The parameters for the entries in the covariance matrix are shown. The names of parameters are displayed in parentheses.
All these parameters are set by default and their names have the prefix _Add. No initial estimates are given as input, as indicated by the missing value '.'.
Output 29.21.2 shows the customized fit summary table, which has been much simplified for the current example due to the uses of some options in the FITINDEX statement.
As shown in Output 29.21.2, the chi-square test statistic is 2.4924. With six degrees of freedom, the test statistic is not significant at 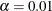 . Therefore, the hypothesized model is supported, which means that the equality of the covariance matrices of the groups is
supported.
. Therefore, the hypothesized model is supported, which means that the equality of the covariance matrices of the groups is
supported.
Instead of using the MSTRUCT modeling language explicitly for defining the hypothesized covariance patterns (or structures), you can also invoke the same covariance patterns by using the COVPATTERN= option, as shown in the following statements:
proc calis covpattern=eqcovmat; var high medium low; group 1 / data=expert nobs=20 label="Expert"; group 2 / data=novice nobs=18 label="Novice"; fitindex NoIndexType On(only)=[chisq df probchi]; run;
The COVPATTERN=EQCOVMAT option in the PROC CALIS statement hypothesizes that the two population covariance matrices for the groups are the same. Next, you specify the set of variables in the covariance matrices in the VAR statement, followed by the specification of the data for the two groups. You use the FITINDEX statement to select a subset of fit indices to display in the output.
Output 29.21.3 shows the data sets and the corresponding MSTRUCT models that are generated by the COVPATTERN=EQCOVMAT option.
Output 29.21.3: Modeling Information with the COVPATTERN=EQCOVMAT Option
PROC CALIS generates Model 1 for the expert group and Model 2 for the novice group. Output 29.21.4 and Output 29.21.5 show the covariance matrices of these two models.
Output 29.21.4: Initial Specification of Model 1 for the Expert Group
Output 29.21.5: Initial Specification of Model 2 for the Novice Group
In Output 29.21.4, the covariance matrix for the expert group has three variables: high, medium, and low. The second table of Output 29.21.4 shows the parameters for the corresponding covariance matrix. PROC CALIS generates the parameter names for the elements in
this covariance matrix: _cov_1_1, _cov_2_1, …, _cov_3_3. In Output 29.21.5, the covariance matrix for the novice group has exactly the same set of three variables: high, medium, and low. The second table of Output 29.21.5 shows the parameters for the corresponding covariance matrix. These variance and covariance parameters are exactly the same
as those in Output 29.21.4, as required by the testing of equality of covariance matrices.
Output 29.21.6 shows the fit summary of the test. The test results are exactly the same as those in Output 29.21.2, as expected. The chi-square value is 2.4924. With six degrees of freedom, the test statistic is not significant at 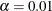 . The hypothesis about the equality of the covariance matrices between the groups is supported.
. The hypothesis about the equality of the covariance matrices between the groups is supported.
Output 29.21.6: Model Fit with the COVPATTERN=EQCOVMAT Option
One advantage of using the built-in covariance patterns such as the current COVPATTERN=EQCOVMAT option is that it is more efficient and less error-prone than if you specify the covariance patterns manually by using the MSTRUCT and MATRIX statements. With the COVPATTERN= option, PROC CALIS generates the correct model specification internally. Another advantage is that when applicable, PROC CALIS applies the appropriate chi-square correction to the chi-square test statistic. For the current example, PROC CALIS displays the following message in the output:
NOTE: The chi-square correction due to Box for testing equality of
covariance matrices was applied. Use the CHICORRECT=0 option
if this correction is not desirable.
This shows that when you use the COVPATTERN=EQCOVMAT option, an appropriate chi-square correction is applied automatically to the chi-square test statistic. To turn off this automatic chi-square, you can use the CHICORRECT=0 in the PROC CALIS statement (although this should be a rare practice with the COVPATTERN= options).
To extend the test of the equality of covariance matrices to the test of the equality of mean vectors, see Example 29.4. To extend the multiple-group analysis of covariance patterns to the multiple-group analysis of a general structural equation model, see Example 29.28.