The CALIS Procedure
-
Overview

-
Getting Started

-
Syntax
 Classes of Statements in PROC CALISSingle-Group Analysis SyntaxMultiple-Group Multiple-Model Analysis SyntaxPROC CALIS StatementBOUNDS StatementBY StatementCOSAN StatementCOV StatementDETERM StatementEFFPART StatementFACTOR StatementFITINDEX StatementFREQ StatementGROUP StatementLINCON StatementLINEQS StatementLISMOD StatementLMTESTS StatementMATRIX StatementMEAN StatementMODEL StatementMSTRUCT StatementNLINCON StatementNLOPTIONS StatementOUTFILES StatementPARAMETERS StatementPARTIAL StatementPATH StatementPATHDIAGRAM StatementPCOV StatementPVAR StatementRAM StatementREFMODEL StatementRENAMEPARM StatementSAS Programming StatementsSIMTESTS StatementSTD StatementSTRUCTEQ StatementTESTFUNC StatementVAR StatementVARIANCE StatementVARNAMES StatementWEIGHT Statement
Classes of Statements in PROC CALISSingle-Group Analysis SyntaxMultiple-Group Multiple-Model Analysis SyntaxPROC CALIS StatementBOUNDS StatementBY StatementCOSAN StatementCOV StatementDETERM StatementEFFPART StatementFACTOR StatementFITINDEX StatementFREQ StatementGROUP StatementLINCON StatementLINEQS StatementLISMOD StatementLMTESTS StatementMATRIX StatementMEAN StatementMODEL StatementMSTRUCT StatementNLINCON StatementNLOPTIONS StatementOUTFILES StatementPARAMETERS StatementPARTIAL StatementPATH StatementPATHDIAGRAM StatementPCOV StatementPVAR StatementRAM StatementREFMODEL StatementRENAMEPARM StatementSAS Programming StatementsSIMTESTS StatementSTD StatementSTRUCTEQ StatementTESTFUNC StatementVAR StatementVARIANCE StatementVARNAMES StatementWEIGHT Statement -
Details
 Input Data SetsOutput Data SetsDefault Analysis Type and Default ParameterizationThe COSAN ModelThe FACTOR ModelThe LINEQS ModelThe LISMOD Model and SubmodelsThe MSTRUCT ModelThe PATH ModelThe RAM ModelNaming Variables and ParametersSetting Constraints on ParametersAutomatic Variable SelectionPath Diagrams: Layout Algorithms, Default Settings, and CustomizationEstimation CriteriaRelationships among Estimation CriteriaGradient, Hessian, Information Matrix, and Approximate Standard ErrorsCounting the Degrees of FreedomAssessment of FitCase-Level Residuals, Outliers, Leverage Observations, and Residual DiagnosticsLatent Variable ScoresTotal, Direct, and Indirect EffectsStandardized SolutionsModification IndicesMissing Values and the Analysis of Missing PatternsMeasures of Multivariate KurtosisInitial EstimatesUse of Optimization TechniquesComputational ProblemsDisplayed OutputODS Table NamesODS Graphics
Input Data SetsOutput Data SetsDefault Analysis Type and Default ParameterizationThe COSAN ModelThe FACTOR ModelThe LINEQS ModelThe LISMOD Model and SubmodelsThe MSTRUCT ModelThe PATH ModelThe RAM ModelNaming Variables and ParametersSetting Constraints on ParametersAutomatic Variable SelectionPath Diagrams: Layout Algorithms, Default Settings, and CustomizationEstimation CriteriaRelationships among Estimation CriteriaGradient, Hessian, Information Matrix, and Approximate Standard ErrorsCounting the Degrees of FreedomAssessment of FitCase-Level Residuals, Outliers, Leverage Observations, and Residual DiagnosticsLatent Variable ScoresTotal, Direct, and Indirect EffectsStandardized SolutionsModification IndicesMissing Values and the Analysis of Missing PatternsMeasures of Multivariate KurtosisInitial EstimatesUse of Optimization TechniquesComputational ProblemsDisplayed OutputODS Table NamesODS Graphics -
Examples
 Estimating Covariances and CorrelationsEstimating Covariances and Means SimultaneouslyTesting Uncorrelatedness of VariablesTesting Covariance PatternsTesting Some Standard Covariance Pattern HypothesesLinear Regression ModelMultivariate Regression ModelsMeasurement Error ModelsTesting Specific Measurement Error ModelsMeasurement Error Models with Multiple PredictorsMeasurement Error Models Specified As Linear EquationsConfirmatory Factor ModelsConfirmatory Factor Models: Some VariationsResidual Diagnostics and Robust EstimationThe Full Information Maximum Likelihood MethodComparing the ML and FIML EstimationPath Analysis: Stability of AlienationSimultaneous Equations with Mean Structures and Reciprocal PathsFitting Direct Covariance StructuresConfirmatory Factor Analysis: Cognitive AbilitiesTesting Equality of Two Covariance Matrices Using a Multiple-Group AnalysisTesting Equality of Covariance and Mean Matrices between Independent GroupsIllustrating Various General Modeling LanguagesTesting Competing Path Models for the Career Aspiration DataFitting a Latent Growth Curve ModelHigher-Order and Hierarchical Factor ModelsLinear Relations among Factor LoadingsMultiple-Group Model for Purchasing BehaviorFitting the RAM and EQS Models by the COSAN Modeling LanguageSecond-Order Confirmatory Factor AnalysisLinear Relations among Factor Loadings: COSAN Model SpecificationOrdinal Relations among Factor LoadingsLongitudinal Factor Analysis
Estimating Covariances and CorrelationsEstimating Covariances and Means SimultaneouslyTesting Uncorrelatedness of VariablesTesting Covariance PatternsTesting Some Standard Covariance Pattern HypothesesLinear Regression ModelMultivariate Regression ModelsMeasurement Error ModelsTesting Specific Measurement Error ModelsMeasurement Error Models with Multiple PredictorsMeasurement Error Models Specified As Linear EquationsConfirmatory Factor ModelsConfirmatory Factor Models: Some VariationsResidual Diagnostics and Robust EstimationThe Full Information Maximum Likelihood MethodComparing the ML and FIML EstimationPath Analysis: Stability of AlienationSimultaneous Equations with Mean Structures and Reciprocal PathsFitting Direct Covariance StructuresConfirmatory Factor Analysis: Cognitive AbilitiesTesting Equality of Two Covariance Matrices Using a Multiple-Group AnalysisTesting Equality of Covariance and Mean Matrices between Independent GroupsIllustrating Various General Modeling LanguagesTesting Competing Path Models for the Career Aspiration DataFitting a Latent Growth Curve ModelHigher-Order and Hierarchical Factor ModelsLinear Relations among Factor LoadingsMultiple-Group Model for Purchasing BehaviorFitting the RAM and EQS Models by the COSAN Modeling LanguageSecond-Order Confirmatory Factor AnalysisLinear Relations among Factor Loadings: COSAN Model SpecificationOrdinal Relations among Factor LoadingsLongitudinal Factor Analysis - References
Assessment of Fit
In PROC CALIS, there are three main tools for assessing model fit:
-
residuals for the fitted means or covariances
-
overall model fit indices
-
squared multiple correlations and determination coefficients
This section contains a collection of formulas for these assessment tools. The following notation is used:
-
N for the total sample size
-
k for the total number of independent groups in analysis
-
p for the number of manifest variables
-
t for the number of parameters to estimate
-
 for the t-vector of parameters,
for the t-vector of parameters,  for the estimated parameters
for the estimated parameters
-
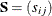 for the
for the 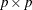 input covariance or correlation matrix
input covariance or correlation matrix
-
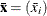 for the p-vector of sample means
for the p-vector of sample means
-
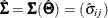 for the predicted covariance or correlation matrix
for the predicted covariance or correlation matrix
-
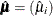 for the predicted mean vector
for the predicted mean vector
-
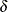 for indicating the modeling of the mean structures
for indicating the modeling of the mean structures
-
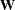 for the weight matrix
for the weight matrix
-
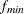 for the minimized function value of the fitted model
for the minimized function value of the fitted model
-
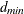 for the degrees of freedom of the fitted model
for the degrees of freedom of the fitted model
In multiple-group analyses, subscripts are used to distinguish independent groups or samples. For example, 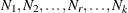 denote the sample sizes for k groups. Similarly, notation such as
denote the sample sizes for k groups. Similarly, notation such as 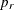 ,
, 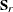 ,
, 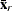 ,
, 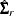 ,
, 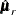 ,
, 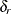 , and
, and 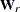 is used for multiple-group situations.
is used for multiple-group situations.
Residuals in the Moment Matrices
Residuals indicate how well each entry or element in the mean or covariance matrix is fitted. Large residuals indicate bad fit.
PROC CALIS computes four types of residuals and writes them to the OUTSTAT= data set when requested.
-
raw residuals
![\[ s_{ij} - \hat{\sigma }_{ij}, \quad \bar{x}_ i-\hat{\mu }_ i \]](images/statug_calis0649.png)
for the covariance and mean residuals, respectively. The raw residuals are displayed whenever the PALL , PRINT , or RESIDUAL option is specified.
-
variance standardized residuals
![\[ \frac{s_{ij} - \hat{\sigma }_{ij}}{\sqrt {s_{ii} s_{jj}}}, \quad \frac{\bar{x}_ i-\hat{\mu }_ i}{\sqrt {s_{ii}}} \]](images/statug_calis0650.png)
for the covariance and mean residuals, respectively. The variance standardized residuals are displayed when you specify one of the following:
The variance standardized residuals are equal to those computed by the EQS 3 program (Bentler 1995).
-
asymptotically standardized residuals
![\[ \frac{s_{ij} - \hat{\sigma }_{ij}}{\sqrt {v_{ij,ij}}} , \quad \frac{\bar{x}_ i-\hat{\mu }_ i}{\sqrt {u_{ii}}} \]](images/statug_calis0651.png)
for the covariance and mean residuals, respectively; with
![\[ v_{ij,ij} = (\hat{\bGamma }_1 - \mb{J}_1 \widehat{\mbox{Cov}}(\hat{\bTheta }) \mb{J}_1^{\prime })_{ij,ij} \]](images/statug_calis0652.png)
![\[ u_{ii} = (\hat{\bGamma }_2 - \mb{J}_2 \widehat{\mbox{Cov}}(\hat{\bTheta }) \mb{J}_2^{\prime })_{ii} \]](images/statug_calis0653.png)
where
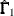 is the
is the 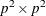 estimated asymptotic covariance matrix of sample covariances,
estimated asymptotic covariance matrix of sample covariances, 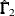 is the
is the 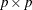 estimated asymptotic covariance matrix of sample means,
estimated asymptotic covariance matrix of sample means, 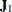 is the
is the 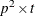 Jacobian matrix
Jacobian matrix 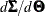 ,
, 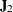 is the
is the 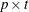 Jacobian matrix
Jacobian matrix 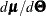 , and
, and 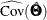 is the
is the 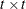 estimated covariance matrix of parameter estimates, all evaluated at the sample moments and estimated parameter values. See
the next section for the definitions of
estimated covariance matrix of parameter estimates, all evaluated at the sample moments and estimated parameter values. See
the next section for the definitions of 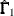 and
and 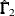 . Asymptotically standardized residuals are displayed when one of the following conditions is met:
. Asymptotically standardized residuals are displayed when one of the following conditions is met:
The asymptotically standardized residuals are equal to those computed by the LISREL 7 program (Jöreskog and Sörbom 1988) except for the denominator in the definition of matrix
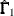 .
.
-
normalized residuals
![\[ \frac{s_{ij} - \hat{\sigma }_{ij}}{\sqrt {(\hat{\bGamma }_1)_{ij,ij}}} , \quad \frac{\bar{x}_ i-\hat{\mu }_ i}{\sqrt {(\hat{\bGamma }_2)_{ii}}} \]](images/statug_calis0665.png)
for the covariance and mean residuals, respectively; with
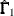 as the
as the 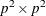 estimated asymptotic covariance matrix of sample covariances; and
estimated asymptotic covariance matrix of sample covariances; and 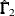 as the
as the 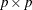 estimated asymptotic covariance matrix of sample means.
estimated asymptotic covariance matrix of sample means.
Diagonal elements of
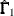 and
and 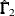 are defined for the following methods:
are defined for the following methods:
-
GLS:
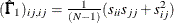 and
and 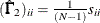
-
ML:
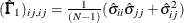 and
and 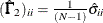
-
WLS:
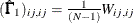 and
and 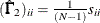
where
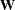 in the WLS method is the weight matrix for the second-order moments.
in the WLS method is the weight matrix for the second-order moments.
Normalized residuals are displayed when one of the following conditions is met:
The normalized residuals are equal to those computed by the LISREL VI program (Jöreskog and Sörbom 1985) except for the definition of the denominator in computing matrix
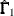 .
.
-
For estimation methods that are not "best" generalized least squares estimators (Browne 1982, 1984), such as METHOD=
NONE, METHOD=
ULS, or METHOD=
DWLS, the assumption of an asymptotic covariance matrix 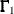 of sample covariances does not seem to be appropriate. In this case, the normalized residuals should be replaced by the more
relaxed variance standardized residuals. Computation of asymptotically standardized residuals requires computing the Jacobian
and information matrices. This is computationally very expensive and is done only if the Jacobian matrix has to be computed
for some other reasons—that is, if at least one of the following items is true:
of sample covariances does not seem to be appropriate. In this case, the normalized residuals should be replaced by the more
relaxed variance standardized residuals. Computation of asymptotically standardized residuals requires computing the Jacobian
and information matrices. This is computationally very expensive and is done only if the Jacobian matrix has to be computed
for some other reasons—that is, if at least one of the following items is true:
-
The default, PRINT , or PALL displayed output is requested, and neither the NOMOD nor NOSTDERR option is specified.
-
Either the MODIFICATION (included in PALL ), PCOVES , or STDERR (included in default, PRINT , and PALL output) option is requested or RESIDUAL =ASYSTAND is specified.
-
The LEVMAR or NEWRAP optimization technique is used.
-
An OUTMODEL= data set is specified without using the NOSTDERR option.
-
An OUTEST= data set is specified without using the NOSTDERR option.
Since normalized residuals use an overestimate of the asymptotic covariance matrix of residuals (the diagonals of 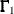 and
and 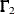 ), the normalized residuals cannot be greater than the asymptotically standardized residuals (which use the diagonal of the
form
), the normalized residuals cannot be greater than the asymptotically standardized residuals (which use the diagonal of the
form 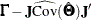 ).
).
Together with the residual matrices, the values of the average residual, the average off-diagonal residual, and the rank order of the largest values are displayed. The distributions of the normalized and standardized residuals are displayed also.
Overall Model Fit Indices
Instead of assessing the model fit by looking at a number of residuals of the fitted moments, an overall model fit index measures model fit by a single number. Although an overall model fit index is precise and easy to use, there are indeed many choices of overall fit indices. Unfortunately, researchers do not always have a consensus on the best set of indices to use in all occasions.
PROC CALIS produces a large number of overall model fit indices in the fit summary table. If you prefer to display only a subset of these fit indices, you can use the ONLIST(ONLY)= option of the FITINDEX statement to customize the fit summary table.
Fit indices are classified into three classes in the fit summary table of PROC CALIS:
-
absolute or standalone Indices
-
parsimony indices
-
incremental indices
Absolute or Standalone Indices
These indices are constructed so that they measure model fit without comparing with a baseline model and without taking the model complexity into account. They measure the absolute fit of the model.
-
fit function or discrepancy function The fit function or discrepancy function F is minimized during the optimization. See the section Estimation Criteria for definitions of various discrepancy functions available in PROC CALIS. For a multiple-group analysis, the fit function can be written as a weighted average of discrepancy functions for k independent groups as:
![\[ F = \sum _{r=1}^ k a_ r F_ r \]](images/statug_calis0674.png)
where
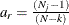 and
and 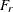 are the group weight and the discrepancy function for the rth group, respectively. Notice that although the groups are assumed to be independent in the model, in general
are the group weight and the discrepancy function for the rth group, respectively. Notice that although the groups are assumed to be independent in the model, in general 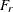 ’s are not independent when F is being minimized. The reason is that
’s are not independent when F is being minimized. The reason is that 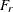 ’s might have shared parameters in
’s might have shared parameters in 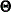 during estimation.
during estimation.
The minimized function value of F will be denoted as
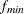 , which is always positive, with small values indicating good fit.
, which is always positive, with small values indicating good fit.
-
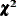 test statistic For ML, GLS, and WLS estimation, the overall
test statistic For ML, GLS, and WLS estimation, the overall 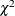 measure for testing model fit is
measure for testing model fit is
![\[ \chi ^2 = (N-k) * f_{\mathit{min}} \]](images/statug_calis0678.png)
where
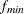 is the function value at the minimum, N is the total sample size, and k is the number of independent groups. The associated degrees of freedom is denoted by
is the function value at the minimum, N is the total sample size, and k is the number of independent groups. The associated degrees of freedom is denoted by 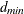 .
.
For ML estimation, this gives the likelihood ratio test statistic of the specified structural model in the null hypothesis against an unconstrained saturated model in the alternative hypothesis. The
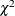 test is valid only if the observations are independent and identically distributed, the analysis is based on the unstandardized
sample covariance matrix
test is valid only if the observations are independent and identically distributed, the analysis is based on the unstandardized
sample covariance matrix 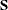 , and the sample size N is sufficiently large (Browne 1982; Bollen 1989b; Jöreskog and Sörbom 1985). For ML and GLS estimates, the variables must also have an approximately multivariate normal distribution.
, and the sample size N is sufficiently large (Browne 1982; Bollen 1989b; Jöreskog and Sörbom 1985). For ML and GLS estimates, the variables must also have an approximately multivariate normal distribution.
In the output fit summary table of PROC CALIS, the notation "Prob > Chi-Square" means "the probability of obtaining a greater
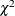 value than the observed value under the null hypothesis." This probability is also known as the p-value of the chi-square test statistic.
value than the observed value under the null hypothesis." This probability is also known as the p-value of the chi-square test statistic.
-
Satorra-Bentler scaled
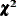 value (Satorra and Bentler 1994)
For MLSB estimation, the baseline and target model
value (Satorra and Bentler 1994)
For MLSB estimation, the baseline and target model 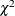 is adjusted by the formula by
is adjusted by the formula by
![\[ \chi ^2_{\mathit{SB}} = \frac{\chi ^2}{\tau /d} \]](images/statug_calis0679.png)
where d is the degrees of freedom of the baseline or target model and
 is a quantity that must be estimated in practice. Raw data are necessary for computing the estimate of
is a quantity that must be estimated in practice. Raw data are necessary for computing the estimate of  . Both d and
. Both d and  are usually different for the baseline and target models. See Satorra and Bentler (1994) for detailed formulas.
are usually different for the baseline and target models. See Satorra and Bentler (1994) for detailed formulas.
When you specify METHOD= MLSB, PROC CALIS displays the scaled chi-squares for the baseline and target models. In addition, various fit indices are computed based on the scaled chi-squares instead of the regular versions. If the formulas for the fit indices involve the fit function values of the baseline and target models, the scaled versions of these function values are used instead.
-
adjusted
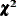 value (Browne 1982) If the variables
are p-variate elliptic rather than normal and have significant amounts of multivariate kurtosis (leptokurtic or platykurtic), the
value (Browne 1982) If the variables
are p-variate elliptic rather than normal and have significant amounts of multivariate kurtosis (leptokurtic or platykurtic), the
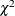 value can be adjusted to
value can be adjusted to
![\[ \chi ^2_{ell} = \frac{\chi ^2}{\eta _2} \]](images/statug_calis0680.png)
where
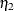 is the multivariate relative kurtosis coefficient.
is the multivariate relative kurtosis coefficient.
-
Z-test (Wilson and Hilferty 1931) The Z-test of Wilson and Hilferty assumes a p-variate normal distribution,
![\[ Z = \frac{\sqrt [3]{\frac{\chi ^2}{d}} - (1 - \frac{2}{9 d})}{\sqrt {\frac{2}{9 d}}} \]](images/statug_calis0682.png)
where d is the degrees of freedom of the model. See McArdle (1988) and Bishop, Fienberg, and Holland (1975, p. 527) for an application of the Z-test.
-
critical N index (Hoelter 1983) The critical N (Hoelter 1983) is defined as
![\[ \mbox{CN} = \mbox{int}(\frac{\chi ^2_{\mathit{crit}}}{f_{\mathit{min}}}) \]](images/statug_calis0683.png)
where
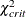 is the critical chi-square value for the given d degrees of freedom and probability
is the critical chi-square value for the given d degrees of freedom and probability 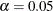 , and int() takes the integer part of the expression. See Bollen (1989b, p. 277). Conceptually, the CN value is the largest number of observations that could still make the chi-square model fit
statistic insignificant if it were to apply to the actual sample fit function value
, and int() takes the integer part of the expression. See Bollen (1989b, p. 277). Conceptually, the CN value is the largest number of observations that could still make the chi-square model fit
statistic insignificant if it were to apply to the actual sample fit function value 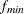 . Hoelter (1983) suggests that CN should be at least 200; however, Bollen (1989b) notes that the CN value might lead to an overly pessimistic assessment of fit for small samples.
. Hoelter (1983) suggests that CN should be at least 200; however, Bollen (1989b) notes that the CN value might lead to an overly pessimistic assessment of fit for small samples.
Note that when you have a perfect model fit for your data (that is,
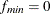 ) or a zero degree of freedom for your model (that is, d = 0), CN is not computable.
) or a zero degree of freedom for your model (that is, d = 0), CN is not computable.
-
root mean square residual (RMR) For a single-group analysis, the RMR is the root of the mean squared residuals:
![\[ \mbox{RMR} = \sqrt {\frac{1}{b} [ \sum _ i^ p \sum _ j^ i (s_{ij} - \hat{\sigma }_{ij})^2 + \delta \sum _ i^ p (\bar{x}_ i - \hat{\mu }_ i)^2 ]} \]](images/statug_calis0687.png)
where
![\[ b = \frac{p(p+1+2 \delta )}{2} \]](images/statug_calis0688.png)
is the number of distinct elements in the covariance matrix and in the mean vector (if modeled).
For multiple-group analysis, PROC CALIS uses the following formula for the overall RMR:
![\[ \mbox{overall RMR} = \sqrt {\sum _{r=1}^ k \frac{w_ r}{\sum _{r=1}^ k w_ r} [ \sum _ i^ p \sum _ j^ i (s_{ij} - \hat{\sigma }_{ij})^2 + \delta \sum _ i^ p (\bar{x}_ i - \hat{\mu }_ i)^2 ] } \]](images/statug_calis0689.png)
where
![\[ w_ r = \frac{N_ r - 1}{N-k} b_ r \]](images/statug_calis0690.png)
is the weight for the squared residuals of the rth group. Hence, the weight
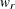 is the product of group size weight
is the product of group size weight 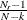 and the number of distinct moments
and the number of distinct moments 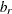 in the rth group.
in the rth group.
-
standardized root mean square residual (SRMR)
For a single-group analysis, the SRMR is the root of the mean of the standardized squared residuals:
![\[ \mbox{SRMR} = \sqrt {\frac{1}{b} [ \sum _ i^ p \sum _ j^ i \frac{(s_{ij} - \hat{\sigma }_{ij})^2}{s_{ii} s_{jj}} + \delta \sum _ i^ p \frac{ (\bar{x}_ i - \hat{\mu }_ i)^2 }{s_{ii}} ] } \]](images/statug_calis0694.png)
where b is the number of distinct elements in the covariance matrix and in the mean vector (if modeled). The formula for b is defined exactly the same way as it appears in the formula for RMR.
Similar to the calculation of the overall RMR, an overall measure of SRMR in a multiple-group analysis is a weighted average of the standardized squared residuals of the groups. That is,
![\[ \mbox{overall SRMR} = \sqrt {\sum _{r=1}^ k \frac{w_ r}{\sum _{r=1}^ k w_ r} [ \sum _ i^ p \sum _ j^ i \frac{(s_{ij} - \hat{\sigma }_{ij})^2}{s_{ii} s_{jj}} + \delta \sum _ i^ p \frac{ (\bar{x}_ i - \hat{\mu }_ i)^2 }{s_{ii}} ]} \]](images/statug_calis0695.png)
where
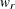 is the weight for the squared residuals of the rth group. The formula for
is the weight for the squared residuals of the rth group. The formula for 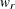 is defined exactly the same way as it appears in the formula for SRMR.
is defined exactly the same way as it appears in the formula for SRMR.
-
goodness-of-fit index (GFI) For a single-group analysis, the goodness-of-fit index for the ULS, GLS, and ML estimation methods is:
![\[ \mr{GFI} = 1 - \frac{\mr{Tr}( (\mb{W}^{-1}(\mb{S} - \hat{\bSigma }))^2)+\delta (\mb{\bar{x}}-\hat{\bmu })^\prime \mb{W}^{-1}(\mb{\bar{x}}-\hat{\bmu })}{\mr{Tr}( (\mb{W}^{-1}\mb{S})^2 )+\delta \mb{\bar{x}}^\prime \mb{W}^{-1}\mb{\bar{x}}} \]](images/statug_calis0696.png)
with
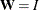 for ULS,
for ULS, 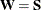 for GLS, and
for GLS, and 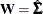 . For WLS and DWLS estimation,
. For WLS and DWLS estimation,
![\[ \mr{GFI} = 1 - \frac{ (\mb{u} - \hat{\bm {\eta }})^{\prime } \mb{W}^{-1} (\mb{u} - \hat{\bm {\eta }})}{\mb{u}^{\prime } \mb{W}^{-1} \mb{u}} \]](images/statug_calis0699.png)
where
 is the vector of observed moments and
is the vector of observed moments and 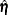 is the vector of fitted moments. When the mean structures are modeled, vectors
is the vector of fitted moments. When the mean structures are modeled, vectors  and
and 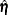 contains all the nonredundant elements
contains all the nonredundant elements 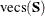 in the covariance matrix and all the means. That is,
in the covariance matrix and all the means. That is,
![\[ \mb{u} = ({\mr{vecs}^\prime (\mb{S}),\mb{\bar{x}}^\prime })^\prime , \quad \hat{\bm {\eta }} = ({\mr{vecs}^\prime (\hat{\bSigma }),\hat{\bmu }^\prime })^\prime \]](images/statug_calis0702.png)
and the symmetric weight matrix
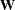 is of dimension
is of dimension 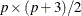 . When the mean structures are not modeled, vectors
. When the mean structures are not modeled, vectors  and
and 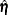 contains all the nonredundant elements
contains all the nonredundant elements 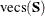 in the covariance matrix only. That is,
in the covariance matrix only. That is,
![\[ \mb{u} = \mr{vecs}(\mb{S}), \quad \hat{\bm {\eta }} = \mr{vecs}(\hat{\bSigma }) \]](images/statug_calis0704.png)
and the symmetric weight matrix
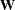 is of dimension
is of dimension 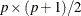 . In addition, for the DWLS estimation,
. In addition, for the DWLS estimation, 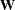 is a diagonal matrix.
is a diagonal matrix.
For a constant weight matrix
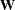 , the goodness-of-fit index is 1 minus the ratio of the minimum function value and the function value before any model has
been fitted. The GFI should be between 0 and 1. The data probably do not fit the model if the GFI is negative or much greater
than 1.
, the goodness-of-fit index is 1 minus the ratio of the minimum function value and the function value before any model has
been fitted. The GFI should be between 0 and 1. The data probably do not fit the model if the GFI is negative or much greater
than 1.
For a multiple-group analysis, individual
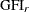 ’s are computed for groups. The overall measure is a weighted average of individual
’s are computed for groups. The overall measure is a weighted average of individual 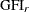 ’s, using weight
’s, using weight 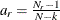 . That is,
. That is,
![\[ \mbox{overall GFI} = \sum _{r=1}^ k a_ r \mbox{GFI}_ r \]](images/statug_calis0708.png)
Parsimony Indices
These indices are constructed so that the model complexity is taken into account when assessing model fit. In general, models with more parameters (fewer degrees of freedom) are penalized.
-
adjusted goodness-of-fit index (AGFI) The AGFI is the GFI adjusted for the degrees of freedom d of the model,
![\[ \mbox{AGFI} = 1 - \frac{c}{d} (1 - \mbox{GFI}) \]](images/statug_calis0709.png)
where
![\[ c = \sum _{r=1}^ k \frac{p_ k (p_ k + 1 + 2 \delta _ k)}{2} \]](images/statug_calis0710.png)
computes the total number of elements in the covariance matrices and mean vectors for modeling. For single-group analyses, the AGFI corresponds to the GFI in replacing the total sum of squares by the mean sum of squares.
Caution:
-
Large p and small d can result in a negative AGFI. For example, GFI=0.90, p=19, and d=2 result in an AGFI of –8.5.
-
AGFI is not defined for a saturated model, due to division by d = 0.
-
AGFI is not sensitive to losses in d.
The AGFI should be between 0 and 1. The data probably do not fit the model if the AGFI is negative or much greater than 1. For more information, see Mulaik et al. (1989).
-
-
parsimonious goodness-of-fit index (PGFI) The PGFI (Mulaik et al. 1989) is a modification of the GFI that takes the parsimony of the model into account:
![\[ \mbox{PGFI} = \frac{d_{\mathit{min}}}{d_0} \mbox{GFI} \]](images/statug_calis0711.png)
where
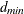 is the model degrees of freedom and
is the model degrees of freedom and 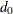 is the degrees of freedom for the independence model. See the section Incremental Indices for the definition of independence model. The PGFI uses the same parsimonious factor as the parsimonious normed Bentler-Bonett
index (James, Mulaik, and Brett 1982).
is the degrees of freedom for the independence model. See the section Incremental Indices for the definition of independence model. The PGFI uses the same parsimonious factor as the parsimonious normed Bentler-Bonett
index (James, Mulaik, and Brett 1982).
-
RMSEA index (Steiger and Lind 1980; Steiger 1998) The root mean square error of approximation (RMSEA) coefficient is:
![\[ \epsilon = \sqrt {k} \sqrt {\max (\frac{f_{\mathit{min}}}{d_{\mathit{min}}} - \frac{1}{(N-k)},0) } \]](images/statug_calis0713.png)
The lower and upper limits of the
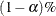 -confidence interval are computed using the cumulative distribution function of the noncentral chi-square distribution
-confidence interval are computed using the cumulative distribution function of the noncentral chi-square distribution 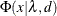 . With
. With 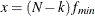 ,
, 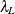 satisfying
satisfying 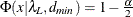 , and
, and 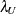 satisfying
satisfying 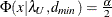 :
:
![\[ (\epsilon _{\alpha _ L} ; \epsilon _{\alpha _ U}) = ( \sqrt {k} \sqrt {\frac{\lambda _ L}{(N-k)d_{\mathit{min}}}} ; \sqrt {k} \sqrt {\frac{\lambda _ U}{(N-k)d_{\mathit{min}}}}) \]](images/statug_calis0721.png)
See Browne and Du Toit (1992) for more details. The size of the confidence interval can be set by the option ALPHARMS=
 ,
, 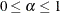 . The default is
. The default is 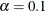 , which corresponds to the 90% confidence interval for the RMSEA.
, which corresponds to the 90% confidence interval for the RMSEA.
-
probability for test of close fit (Browne and Cudeck 1993) The traditional exact
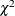 test hypothesis
test hypothesis 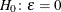 is replaced by the null hypothesis of close fit
is replaced by the null hypothesis of close fit 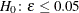 and the exceedance probability P is computed as:
and the exceedance probability P is computed as:
![\[ P = 1 - \Phi (x|\lambda ^*,d_{\mathit{min}}) \]](images/statug_calis0724.png)
where
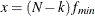 and
and 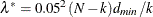 . The null hypothesis of close fit is rejected if P is smaller than a prespecified level (for example, P < 0.05).
. The null hypothesis of close fit is rejected if P is smaller than a prespecified level (for example, P < 0.05).
-
ECVI: expected cross-validation index (Browne and Cudeck 1993) The following formulas for ECVI are limited to the case of single-sample analysis without mean structures and with either the GLS, ML, or WLS estimation method. For other cases, ECVI is not defined in PROC CALIS. For GLS and WLS, the estimator c of the ECVI is linearly related to AIC, Akaike’s Information Criterion (Akaike 1974, 1987):
![\[ c = f_{\mathit{min}} + \frac{2t}{N-1} \]](images/statug_calis0726.png)
For ML estimation,
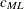 is used:
is used:
![\[ c_{\mathit{ML}} = f_{\mathit{min}} + \frac{2t}{N-p-2} \]](images/statug_calis0728.png)
For GLS and WLS, the confidence interval
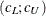 for ECVI is computed using the cumulative distribution function
for ECVI is computed using the cumulative distribution function 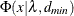 of the noncentral chi-square distribution,
of the noncentral chi-square distribution,
![\[ (c_ L ; c_ U) = (\frac{\lambda _ L + p(p+1)/2 + t}{(N-1)} ; \frac{\lambda _ U + p(p+1)/2 + t}{(N-1)}) \]](images/statug_calis0731.png)
with
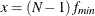 ,
, 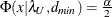 , and
, and 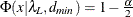 .
.
For ML, the confidence interval
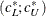 for ECVI is:
for ECVI is:
![\[ (c^*_ L ; c^*_ U) = (\frac{\lambda ^*_ L + p(p+1)/2 + t}{N-p-2} ; \frac{\lambda ^*_ U + p(p+1)/2 + t}{N-p-2}) \]](images/statug_calis0736.png)
where
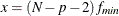 ,
, 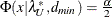 and
and 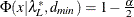 . See Browne and Cudeck (1993). The size of the confidence interval can be set by the option ALPHAECV=
. See Browne and Cudeck (1993). The size of the confidence interval can be set by the option ALPHAECV=
 ,
, 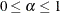 . The default is
. The default is 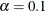 , which corresponds to the 90% confidence interval for the ECVI.
, which corresponds to the 90% confidence interval for the ECVI.
-
Akaike’s information criterion (AIC) (Akaike 1974, 1987) This is a criterion for selecting the best model among a number of candidate models. The model that yields the smallest value of AIC is considered the best.
![\[ \mbox{AIC} = h + 2t \]](images/statug_calis0740.png)
where h is the –2 times the likelihood function value for the FIML method or the
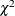 value for other estimation methods.
value for other estimation methods.
-
consistent Akaike’s information criterion (CAIC) (Bozdogan 1987) This is another criterion, similar to AIC, for selecting the best model among alternatives. The model that yields the smallest value of CAIC is considered the best. CAIC is preferred by some people to AIC or the
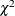 test.
test.
![\[ \mbox{CAIC} = h + (\ln (N) + 1) t \]](images/statug_calis0741.png)
where h is the –2 times the likelihood function value for the FIML method or the
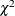 value for other estimation methods. Notice that N includes the number of incomplete observations for the FIML method while it includes only the complete observations for other
estimation methods.
value for other estimation methods. Notice that N includes the number of incomplete observations for the FIML method while it includes only the complete observations for other
estimation methods.
-
Schwarz’s Bayesian criterion (SBC) (Schwarz 1978; Sclove 1987) This is another criterion, similar to AIC, for selecting the best model. The model that yields the smallest value of SBC is considered the best. SBC is preferred by some people to AIC or the
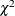 test.
test.
![\[ \mbox{SBC} = h + \ln (N) t \]](images/statug_calis0742.png)
where h is the –2 times the likelihood function value for the FIML method or the
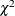 value for other estimation methods. Notice that N includes the number of incomplete observations for the FIML method while it includes only the complete observations for other
estimation methods.
value for other estimation methods. Notice that N includes the number of incomplete observations for the FIML method while it includes only the complete observations for other
estimation methods.
-
McDonald’s measure of centrality (McDonald and Marsh 1988)
![\[ \mbox{CENT} = \mbox{exp}( - \frac{(\chi ^2 - d_{\mathit{min}})}{2N} ) \]](images/statug_calis0743.png)
Incremental Indices
These indices are constructed so that the model fit is assessed through the comparison with a baseline model. The baseline model is usually the independence model where all covariances among manifest variables are assumed to be zeros. The only parameters in the independence model are the diagonals of covariance matrix. If modeled, the mean structures are saturated in the independence model. For multiple-group analysis, the overall independence model consists of component independence models for each group.
In the following, let 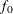 and
and 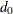 denote the minimized discrepancy function value and the associated degrees of freedom, respectively, for the independence
model; and
denote the minimized discrepancy function value and the associated degrees of freedom, respectively, for the independence
model; and 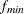 and
and 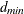 denote the minimized discrepancy function value and the associated degrees of freedom, respectively, for the model being
fitted in the null hypothesis.
denote the minimized discrepancy function value and the associated degrees of freedom, respectively, for the model being
fitted in the null hypothesis.
-
Bentler comparative fit index (Bentler 1995)
![\[ \mbox{CFI} = 1 - \frac{\max ((N-k)f_{\mathit{min}}-d_{\mathit{min}},0)}{\max ((N-k)f_{\mathit{min}}-d_{\mathit{min}},\max ((N-k)f_0-d_0,0)} \]](images/statug_calis0745.png)
-
Bentler-Bonett normed fit index (NFI) (Bentler and Bonett 1980)
![\[ \Delta = \frac{f_0 - f_{\mathit{min}}}{f_0} \quad \]](images/statug_calis0746.png)
Mulaik et al. (1989) recommend the parsimonious weighted form called parsimonious normed fit index (PNFI) (James, Mulaik, and Brett 1982).
-
Bentler-Bonett nonnormed coefficient (Bentler and Bonett 1980)
![\[ \rho = \frac{{f_0 / d_0 - f_{\mathit{min}} / d_{\mathit{min}}}}{{f_0 / d_0 - 1 / (N-k) }} \]](images/statug_calis0747.png)
See Tucker and Lewis (1973).
-
normed index
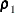 (Bollen 1986)
(Bollen 1986)
![\[ \rho _1 = \frac{{ f_0 / d_0 - f_{\mathit{min}} / d_{\mathit{min}}}}{{f_0 / d_0} } \]](images/statug_calis0749.png)
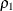 is always less than or equal to 1;
is always less than or equal to 1; 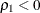 is unlikely in practice. See the discussion in Bollen (1989a).
is unlikely in practice. See the discussion in Bollen (1989a).
-
nonnormed index
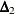 (Bollen 1989a)
(Bollen 1989a)
![\[ \Delta _2 = \frac{{f_0 - f_{\mathit{min}}}}{{f_0 - \frac{d_{\mathit{min}}}{(N-k)}}} \]](images/statug_calis0752.png)
is a modification of Bentler and Bonett’s
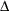 that uses d and "lessens the dependence" on N. See the discussion in (Bollen 1989b).
that uses d and "lessens the dependence" on N. See the discussion in (Bollen 1989b). 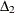 is identical to the IFI2 index of Mulaik et al. (1989).
is identical to the IFI2 index of Mulaik et al. (1989).
-
parsimonious normed fit index (James, Mulaik, and Brett 1982) The PNFI is a modification of Bentler-Bonett’s normed fit index that takes parsimony of the model into account,
![\[ \mbox{PNFI} = \frac{d_{\mathit{min}}}{d_0} \frac{(f_0 - f_{\mathit{min}})}{f_0} \quad \]](images/statug_calis0755.png)
The PNFI uses the same parsimonious factor as the parsimonious GFI of Mulaik et al. (1989).
Fit Indices and Estimation Methods
Note that not all fit indices are reasonable or appropriate for all estimation methods set by the METHOD= option of the PROC CALIS statement. The availability of fit indices is summarized as follows:
-
Adjusted (elliptic) chi-square and its probability are available only for METHOD= ML or GLS and with the presence of raw data input.
-
For METHOD= ULS or DWLS, probability of the chi-square value, RMSEA and its confidence intervals, probability of close fit, ECVI and its confidence intervals, critical N index, Z-test, AIC, CAIC, SBC, and measure of centrality are not appropriate and therefore not displayed.
Individual Fit Indices for Multiple Groups
When you compare the fits of individual groups in a multiple-group analysis, you can examine the residuals of the groups to gauge which group is fitted better than the others. While examining residuals is good for knowing specific locations with inadequate fit, summary measures like fit indices for individual groups would be more convenient for overall comparisons among groups.
Although the overall fit function is a weighted sum of individual fit functions for groups, these individual functions are
not statistically independent. Therefore, in general you cannot partition the degrees of freedom or 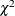 value according to the groups. This eliminates the possibility of breaking down those fit indices that are functions of degrees
of freedom or
value according to the groups. This eliminates the possibility of breaking down those fit indices that are functions of degrees
of freedom or 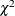 for group comparison purposes. Bearing this fact in mind, PROC CALIS computes only a limited number of descriptive fit indices
for individual groups.
for group comparison purposes. Bearing this fact in mind, PROC CALIS computes only a limited number of descriptive fit indices
for individual groups.
-
fit function The overall fit function is:
![\[ F = \sum _{r=1}^ k a_ r F_ r \]](images/statug_calis0674.png)
where
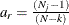 and
and 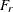 are the group weight and the discrepancy function for group r, respectively. The value of unweighted fit function
are the group weight and the discrepancy function for group r, respectively. The value of unweighted fit function 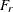 for the rth group is denoted by:
for the rth group is denoted by:
![\[ f_ r \]](images/statug_calis0756.png)
This
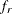 value provides a measure of fit in the rth group without taking the sample size into account. The large the
value provides a measure of fit in the rth group without taking the sample size into account. The large the 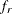 , the worse the fit for the group.
, the worse the fit for the group.
-
percentage contribution to the chi-square The percentage contribution of group r to the chi-square is:
![\[ \mbox{percentage contribution} = a_ r f_ r / f_{\mathit{min}} \times 100\% \]](images/statug_calis0758.png)
where
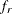 is the value of
is the value of 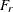 with F minimized at the value
with F minimized at the value 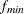 . This percentage value provides a descriptive measure of fit of the moments in group r, weighted by its sample size. The group with the largest percentage contribution accounts for the most lack of fit in the
overall model.
. This percentage value provides a descriptive measure of fit of the moments in group r, weighted by its sample size. The group with the largest percentage contribution accounts for the most lack of fit in the
overall model.
-
root mean square residual (RMR) For the rth group, the total number of moments being modeled is:
![\[ g = \frac{p_ r(p_ r+1+2 \delta _ r)}{2} \]](images/statug_calis0759.png)
where
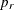 is the number of variables and
is the number of variables and 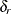 is the indicator variable of the mean structures in the rth group. The root mean square residual for the rth group is:
is the indicator variable of the mean structures in the rth group. The root mean square residual for the rth group is:
![\[ \mbox{RMR}_ r = \sqrt { \frac{1}{g} [ \sum _ i^{p_ r} \sum _ j^ i ([\mb{S}_ r]_{ij} - [\hat{\bSigma }_ r]_{ij})^2 + \delta _ r \sum _ i^{p_ r} ([\mb{\bar{x}}_ r]_ i - [\hat{\bmu }_ r]_ i)^2 ]} \]](images/statug_calis0760.png)
-
standardized root mean square residual (SRMR) For the rth group, the standardized root mean square residual is:
![\[ \mbox{SRMR} = \sqrt { \frac{1}{g} [ \sum _ i^{p_ r} \sum _ j^ i \frac{([\mb{S}_ r]_{ij} - [\hat{\bSigma }_ r]_{ij})^2}{[\mb{S}_ r]_{ii} [\mb{S}_ r]_{jj}} + \delta _ r \sum _ i^{p_ r} \frac{([\mb{\bar{x}}_ r]_ i - [\hat{\bmu }_ r]_ i)^2}{[\mb{S}_ r]_{ii}} ] } \]](images/statug_calis0761.png)
-
goodness-of-fit index (GFI) For the ULS, GLS, and ML estimation, the goodness-of-fit index (GFI) for the rth group is:
![\[ \mr{GFI} = 1 - \frac{\mr{Tr}( (\mb{W}_ r^{-1}(\mb{S}_ r - \hat{\bSigma _ r}))^2)+\delta _ r(\mb{\bar{x}}_ r-\hat{\mb{u}_ r})^\prime \mb{W}_ r^{-1}(\mb{\bar{x}}_ r-\hat{\mb{u}_ r})}{\mr{Tr}( (\mb{W}_ r^{-1}\mb{S}_ r)^2 )+\delta _ r\mb{\bar{x}}_ r^\prime \mb{W}_ r^{-1}\mb{\bar{x}}_ r} \]](images/statug_calis0762.png)
with
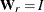 for ULS,
for ULS, 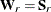 for GLS, and
for GLS, and 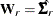 . For the WLS and DWLS estimation,
. For the WLS and DWLS estimation,
![\[ \mr{GFI} = 1 - \frac{ (\mb{u}_ r - \hat{\bm {\eta }}_ r)^{\prime } \mb{W}_ r^{-1} (\mb{u}_ r - \hat{\bm {\eta }_ r})}{\mb{u}_ r^{\prime } \mb{W}_ r^{-1} \mb{u}_ r} \]](images/statug_calis0766.png)
where
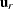 is the vector of observed moments and
is the vector of observed moments and 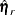 is the vector of fitted moments for the rth group (
is the vector of fitted moments for the rth group (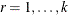 ).
).
When the mean structures are modeled, vectors
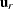 and
and 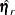 contain all the nonredundant elements
contain all the nonredundant elements 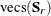 in the covariance matrix and all the means, and
in the covariance matrix and all the means, and 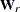 is the weight matrix for covariances and means. When the mean structures are not modeled,
is the weight matrix for covariances and means. When the mean structures are not modeled, 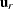 ,
, 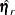 , and
, and 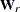 contain elements pertaining to the covariance elements only. Basically, formulas presented here are the same as the case
for a single-group GFI. The only thing added here is the subscript r to denote individual group measures.
contain elements pertaining to the covariance elements only. Basically, formulas presented here are the same as the case
for a single-group GFI. The only thing added here is the subscript r to denote individual group measures.
-
Bentler-Bonett normed fit index (NFI) For the rth group, the Bentler-Bonett NFI is:
![\[ \Delta _ r = \frac{f_{0r} - f_ r}{f_{0r}} \]](images/statug_calis0772.png)
where
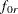 is the function value for fitting the independence model to the rth group. The larger the value of
is the function value for fitting the independence model to the rth group. The larger the value of 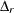 , the better is the fit for the group. Basically, the formula here is the same as the overall Bentler-Bonett NFI. The only
difference is that the subscript r is added to denote individual group measures.
, the better is the fit for the group. Basically, the formula here is the same as the overall Bentler-Bonett NFI. The only
difference is that the subscript r is added to denote individual group measures.
Squared Multiple Correlations and Determination Coefficients
In the section, squared multiple correlations for endogenous variables are defined. Squared multiple correlation is computed for all of these five estimation methods: ULS, GLS, ML, WLS, and DWLS. These coefficients are also computed as in the LISREL VI program of Jöreskog and Sörbom (1985). The DETAE, DETSE, and DETMV determination coefficients are intended to be multivariate generalizations of the squared multiple correlations for different subsets of variables. These coefficients are displayed only when you specify the PDETERM option.
-
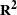 values corresponding to endogenous variables
values corresponding to endogenous variables
![\[ R^2 = 1 - \frac{\widehat{\mbox{Evar}}(y)}{\widehat{\mbox{Var}}(y) } \]](images/statug_calis0776.png)
where y denotes an endogenous variable,
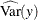 denotes its variance, and
denotes its variance, and 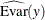 denotes its error (or unsystematic) variance. The variance and error variance are estimated under the model.
denotes its error (or unsystematic) variance. The variance and error variance are estimated under the model.
-
total determination of all equations
![\[ \mbox{DETAE} = 1 - \frac{|\widehat{\mbox{Ecov}}(\mb{y},\bm {\eta })|}{|\widehat{\mbox{Cov}}(\mb{y},\bm {\eta })|} \]](images/statug_calis0779.png)
where the
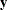 vector denotes all manifest dependent variables, the
vector denotes all manifest dependent variables, the 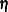 vector denotes all latent dependent variables,
vector denotes all latent dependent variables, 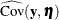 denotes the covariance matrix of
denotes the covariance matrix of 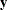 and
and 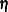 , and
, and 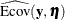 denotes the error covariance matrix of
denotes the error covariance matrix of 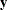 and
and 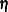 . The covariance matrices are estimated under the model.
. The covariance matrices are estimated under the model.
-
total determination of latent equations
![\[ \mbox{DETSE} = 1 - \frac{|\widehat{\mbox{Ecov}}(\bm {\eta })|}{|\widehat{\mbox{Cov}}(\bm {\eta })|} \]](images/statug_calis0782.png)
where the
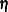 vector denotes all latent dependent variables,
vector denotes all latent dependent variables, 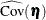 denotes the covariance matrix of
denotes the covariance matrix of 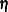 , and
, and 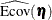 denotes the error covariance matrix of
denotes the error covariance matrix of 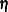 . The covariance matrices are estimated under the model.
. The covariance matrices are estimated under the model.
-
total determination of the manifest equations
![\[ \mbox{DETMV} = 1 - \frac{|\widehat{\mbox{Ecov}}(\mb{y})|}{|\widehat{\mbox{Cov}}(\mb{y})|} \]](images/statug_calis0785.png)
where the
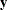 vector denotes all manifest dependent variables,
vector denotes all manifest dependent variables, 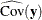 denotes the covariance matrix of
denotes the covariance matrix of 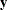 ,
, 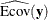 denotes the error covariance matrix of
denotes the error covariance matrix of 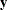 , and
, and 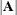 denotes the determinant of matrix
denotes the determinant of matrix 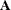 . All the covariance matrices in the formula are estimated under the model.
. All the covariance matrices in the formula are estimated under the model.
You can also use the DETERM statement to request the computations of determination coefficients for any subsets of dependent variables.