The CALIS Procedure

Gradient, Hessian, Information Matrix, and Approximate Standard Errors

Subsections:

Satorra-Bentler Sandwich Formula for Standard Errors
Multiple-Group Extensions
Testing Rank Deficiency in the Approximate Covariance Matrix for Parameter Estimates

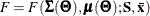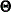For a single-sample setting with a discrepancy function $F=F(\bSigma (\bTheta ),\bmu (\bTheta );\mb{S},\mb{\bar{x}})$ , the gradient is defined as the first partial derivatives of the discrepancy function with respect to the model parameters $\bTheta$ :

$g(\bTheta ) = \frac{\partial }{\partial \bTheta } F(\bTheta )$

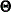The Hessian is defined as the second partial derivatives of the discrepancy function with respect to the model parameters $\bTheta$ :

$H(\bTheta ) = \frac{\partial ^2 }{\partial \bTheta \partial \bTheta ^{\prime }} F(\bTheta )$

Suppose that the mean and covariance structures fit perfectly with 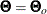$\bTheta =\bTheta _ o$ in the population. The expected information matrix is defined as

$I(\bTheta _ o) = \frac{1}{2} \mathcal{E}(H(\bTheta _ o))$

where the expectation 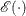$\mathcal{E}(\cdot )$ is taken over the sampling space of 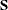$\mb{S}$ and $\mb{\bar{x}}$ . Hence, the expected information matrix 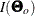$I(\bTheta _ o)$ does not contain any sample values.

The expected information matrix plays a significant role in statistical theory. Under certain regularity conditions, the inverse of the information matrix 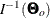$I^{-1}(\bTheta _ o)$ is the asymptotic covariance matrix for 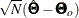$\sqrt {N}(\hat{\bTheta }-\bTheta _ o)$ , where N denotes the sample size and 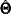$\hat{\bTheta }$ is an estimator.

In practice, 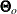$\bTheta _ o$ is never known and can only be estimated. The information matrix is therefore evaluating at the sample estimate 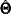$\hat{\bTheta }$ and is denoted as

$I(\hat{\bTheta })$

This is the information matrix that PROC CALIS displays in the output.

For a sample of size N, PROC CALIS computes the estimated covariance matrix of 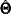$\hat{\bTheta }$ by

$((N-1)I(\hat{\bTheta }))^{-1}$

It then computes approximate standard errors for 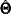$\hat{\bTheta }$ as the square roots of the diagonal elements of this estimated covariance matrix. This formula is based on the expected information and is the default standard error method (INFORMATION=EXP ) for the ML, MLSB, GLS, and WLS estimation methods.

In contrast, by default the FIML estimation method computes standard error estimates based on the so-called observed information matrix (INFORMATION=OBS ), which is defined as

$I_{\mathit{obs}}(\bTheta _ o) = \frac{1}{2} H(\bTheta _ o)$

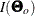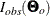The critical difference between $I(\bTheta _ o)$ and $I_{\mathit{obs}}(\bTheta _ o)$ is that the latter does not take the expectation of 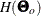$H(\bTheta _ o)$ over the distribution of sample statistics. Kenward and Molenberghs (1998) show that the use of the expected information leads to biased standard errors when the missing data mechanism satisfies only the missing at random (MAR; see Rubin 1976) condition but not the missing completely at random (MCAR) condition. Under the MAR condition, the observed information matrix is the correct choice. Because the FIML estimation is mostly applied when the data contain missing values, using the observed information by default is quite reasonable.

In practice, the observed information is computed by

$I_{\mathit{obs}}(\hat{\bTheta })$

and the estimated covariance matrix of 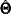$\hat{\bTheta }$ is given by

$((N-1)I_{\mathit{obs}}(\hat{\bTheta }))^{-1}$

However, PROC CALIS does not compute 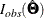$I_{\mathit{obs}}(\hat{\bTheta })$ analytically. It computes 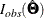$I_{\mathit{obs}}(\hat{\bTheta })$ by the finite-difference method based on the analytic formulas of the first-order partial derivatives of F.

Finally, PROC CALIS does not compute standard errors when you use the ULS and DWLS estimation methods.

If a particular information matrix is singular, PROC CALIS offers two ways to compute a generalized inverse of the matrix and, therefore, two ways to compute approximate standard errors of implicitly constrained parameter estimates, t values , and modification indices . Depending on the G4= specification, either a Moore-Penrose inverse or a G2 inverse is computed. The computationally expensive Moore-Penrose inverse calculates an estimate of the null space by using an eigenvalue decomposition. The computationally cheaper G2 inverse is produced by sweeping the linearly independent rows and columns and zeroing out the dependent ones.

Satorra-Bentler Sandwich Formula for Standard Errors

In addition to the scaled chi-square statistics, Satorra and Bentler (1994) propose the so-called sandwich formula for computing standard errors. For ML estimation, let 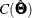$C(\hat{\bTheta })$ be the estimated covariance matrix of the parameter estimates, obtained through either the expected or observed information matrix formula. The Satorra-Bentler sandwich formula for the estimated covariance matrix is of the form

$C_{\mathit{SB}}(\hat{\bTheta }) = C(\hat{\bTheta })\bUpsilon (\hat{\bSigma })C(\hat{\bTheta })$

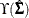where $\Upsilon (\hat{\bSigma })$ depends on the model Jacobian, the weight matrix under the normal distribution theory, and the weight matrix under general distribution theory—all evaluated at the sample estimates or the sample data values. See Satorra and Bentler (1994) for detailed formulas.

If you specify METHOD= MLSB, PROC CALIS uses the Satorra-Bentler sandwich formula to compute standard error estimates. For all other estimation methods that can produce standard error estimates, it uses the unadjusted formula by default. To use the unadjusted formula for METHOD=MLSB, you can specify the SE= UNADJ option. To use the Satorra-Bentler sandwich formula for regular ML estimation, you can specify the SE= SBSW option.

Theoretically, if the population is truly multivariate normal, the weight matrix under normal distribution theory is correctly specified. Asymptotically, the first two terms in the formula for 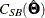$C_{\mathit{SB}}(\hat{\bTheta })$ cancel out, so that

$C_{\mathit{SB}}(\hat{\bTheta }) = C(\hat{\bTheta })$

That is, you can use the unadjusted covariance formula to compute standard error estimates if the multivariate normality assumption is satisfied.

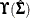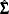If the multivariate normal assumption is not true, then the full sandwich formula has to be involved. Specifically, the middle term, $\bUpsilon (\hat{\bSigma })$ , in the sandwich formula needs to compute the normal-theory weight matrix and other quantities. Because the normal-theory weight matrix is a function of $\hat{\bSigma }$ , evaluation of 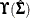$\bUpsilon (\hat{\bSigma })$ depends on the choice of 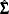$\hat{\bSigma }$ . PROC CALIS uses the model-predicted covariance matrix by default (SBNTW= PRED). You can also use the sample covariance matrix by specifying the SBNTW= OBS option.

Multiple-Group Extensions

In the section Multiple-Group Discrepancy Function, the overall discrepancy function for multiple-group analysis is defined. The same notation is applied here. To begin with, the overall discrepancy function 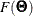$F(\bTheta )$ is expressed as a weighted sum of individual discrepancy functions 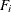$F_ i$ ’s for the groups as follows:

$F(\bTheta ) = \sum _{i=1}^ k t_ i F_ i(\bTheta )$

where

$t_ i = \frac{N_ i-1}{N-k}$

is the weight for group i,

$N = \sum _{i=1}^ k N_ i$

is the total sample size, and 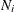$N_ i$ is the sample size for group i.

The gradient 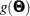$g(\bTheta )$ and the Hessian 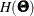$H(\bTheta )$ are now defined as weighted sum of individual functions. That is,

$g(\bTheta ) = \sum _{i=1}^ k t_ i g_ i(\bTheta ) = \sum _{i=1}^ k t_ i \frac{\partial }{\partial \bTheta } F_ i(\bTheta )$

and

$H(\bTheta ) = \sum _{i=1}^ k t_ i H_ i(\bTheta ) = \sum _{i=1}^ k t_ i \frac{\partial ^2 }{\partial \bTheta \partial \bTheta ^{\prime }} F_ i(\bTheta )$

Suppose that the mean and covariance structures fit perfectly with 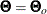$\bTheta =\bTheta _ o$ in the population. If each 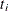$t_ i$ converges to a fixed constant 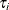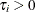$\tau _ i$ ( $\tau _ i > 0$ ) with increasing total sample size, the expected information matrix can be written as:

$I(\bTheta _ o) = \frac{1}{2} \sum _{i=1}^ k \tau _ i \mathcal{E}(H_ i(\bTheta _ o))$

To compute the expected information empirically, 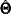$\hat{\bTheta }$ replaces 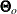$\bTheta _ o$ in the formula.

PROC CALIS computes the estimated covariance matrix of 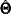$\hat{\bTheta }$ by:

$((N-k)I(\hat{\bTheta }))^{-1}$

Approximate standard errors for 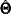$\hat{\bTheta }$ are then computed as the square roots of the diagonal elements of this estimated covariance matrix.

Again, by default the ML, MLSB, GLS, and WLS estimation use such an expected-information based method in the multiple-group setting. For the FIML estimation, the default standard error method is based on the observed information, which is defined as:

$I_{\mathit{obs}}(\bTheta _ o) = \frac{1}{2} \sum _{i=1}^ k \tau _ i H_ i(\bTheta _ o)$

Similar to the single-group analysis, standard errors are not computed with the ULS and DWLS estimation methods in the multiple-group setting.

Testing Rank Deficiency in the Approximate Covariance Matrix for Parameter Estimates

When computing the approximate covariance matrix and hence the standard errors for the parameter estimates, inversion of the scaled information matrix or Hessian matrix is involved. The numerical condition of the information matrix can be very poor in many practical applications, especially for the analysis of unscaled covariance data. The following four-step strategy is used for the inversion of the information matrix.

The inversion (usually of a normalized matrix 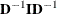$\mb{D}^{-1}\mb{I}\mb{D}^{-1}$ ) is tried using a modified form of the Bunch and Kaufman (1977) algorithm, which allows the specification of a different singularity criterion for each pivot. The following three criteria for the detection of rank loss in the information matrix are used to specify thresholds:
- ASING specifies absolute singularity.
- MSING specifies relative singularity depending on the whole matrix norm.
- VSING specifies relative singularity depending on the column matrix norm.
If no rank loss is detected, the inverse of the information matrix is used for the covariance matrix of parameter estimates, and the next two steps are skipped.
The linear dependencies among the parameter subsets are displayed based on the singularity criteria.
If the number of parameters t is smaller than the value specified by the G4= option (the default value is 60), the Moore-Penrose inverse is computed based on the eigenvalue decomposition of the information matrix. If you do not specify the NOPRINT option, the distribution of eigenvalues is displayed, and those eigenvalues that are set to zero in the Moore-Penrose inverse are indicated. You should inspect this eigenvalue distribution carefully.
If PROC CALIS did not set the right subset of eigenvalues to zero, you can specify the COVSING= option to set a larger or smaller subset of eigenvalues to zero in a further run of PROC CALIS.