The MCMC Procedure
-
Overview

-
Getting Started

-
Syntax

-
Details
 How PROC MCMC WorksBlocking of ParametersSampling MethodsTuning the Proposal DistributionDirect SamplingConjugate SamplingInitial Values of the Markov ChainsAssignments of ParametersStandard DistributionsUsage of Multivariate DistributionsSpecifying a New DistributionUsing Density Functions in the Programming StatementsTruncation and CensoringSome Useful SAS FunctionsMatrix Functions in PROC MCMCCreate Design MatrixModeling Joint LikelihoodAccess Lag and Lead VariablesCALL ODE and CALL QUAD SubroutinesRegenerating Diagnostics PlotsCaterpillar PlotAutocall Macros for PostprocessingGamma and Inverse-Gamma DistributionsPosterior Predictive DistributionHandling of Missing DataFunctions of Random-Effects ParametersFloating Point Errors and OverflowsHandling Error MessagesComputational ResourcesDisplayed OutputODS Table NamesODS Graphics
How PROC MCMC WorksBlocking of ParametersSampling MethodsTuning the Proposal DistributionDirect SamplingConjugate SamplingInitial Values of the Markov ChainsAssignments of ParametersStandard DistributionsUsage of Multivariate DistributionsSpecifying a New DistributionUsing Density Functions in the Programming StatementsTruncation and CensoringSome Useful SAS FunctionsMatrix Functions in PROC MCMCCreate Design MatrixModeling Joint LikelihoodAccess Lag and Lead VariablesCALL ODE and CALL QUAD SubroutinesRegenerating Diagnostics PlotsCaterpillar PlotAutocall Macros for PostprocessingGamma and Inverse-Gamma DistributionsPosterior Predictive DistributionHandling of Missing DataFunctions of Random-Effects ParametersFloating Point Errors and OverflowsHandling Error MessagesComputational ResourcesDisplayed OutputODS Table NamesODS Graphics -
Examples
 Simulating Samples From a Known DensityBox-Cox TransformationLogistic Regression Model with a Diffuse PriorLogistic Regression Model with Jeffreys’ PriorPoisson RegressionNonlinear Poisson Regression ModelsLogistic Regression Random-Effects ModelNonlinear Poisson Regression Multilevel Random-Effects ModelMultivariate Normal Random-Effects ModelMissing at Random AnalysisNonignorably Missing Data (MNAR) AnalysisChange Point ModelsExponential and Weibull Survival AnalysisTime Independent Cox ModelTime Dependent Cox ModelPiecewise Exponential Frailty ModelNormal Regression with Interval CensoringConstrained AnalysisImplement a New Sampling AlgorithmUsing a Transformation to Improve MixingGelman-Rubin DiagnosticsOne-Compartment Model with Pharmacokinetic Data
Simulating Samples From a Known DensityBox-Cox TransformationLogistic Regression Model with a Diffuse PriorLogistic Regression Model with Jeffreys’ PriorPoisson RegressionNonlinear Poisson Regression ModelsLogistic Regression Random-Effects ModelNonlinear Poisson Regression Multilevel Random-Effects ModelMultivariate Normal Random-Effects ModelMissing at Random AnalysisNonignorably Missing Data (MNAR) AnalysisChange Point ModelsExponential and Weibull Survival AnalysisTime Independent Cox ModelTime Dependent Cox ModelPiecewise Exponential Frailty ModelNormal Regression with Interval CensoringConstrained AnalysisImplement a New Sampling AlgorithmUsing a Transformation to Improve MixingGelman-Rubin DiagnosticsOne-Compartment Model with Pharmacokinetic Data - References
Example 73.7 Logistic Regression Random-Effects Model
This example illustrates how you can use PROC MCMC to fit random-effects models. In the example Random-Effects Model in Getting Started: MCMC Procedure, you already saw PROC MCMC fit a linear random-effects model. This example shows how to fit a logistic random-effects model in PROC MCMC. Although you can use PROC MCMC to analyze random-effects models, you might want to first consider some other SAS procedures. For example, you can use PROC MIXED (see Chapter 77: The MIXED Procedure) to analyze linear mixed effects models, PROC NLMIXED (see Chapter 82: The NLMIXED Procedure) for nonlinear mixed effects models, and PROC GLIMMIX (see Chapter 45: The GLIMMIX Procedure) for generalized linear mixed effects models. In addition, a sampling-based Bayesian analysis is available in the MIXED procedure through the PRIOR statement (see PRIOR Statement in Chapter 77: The MIXED Procedure).
The data are taken from Crowder (1978). The Seeds data set is a 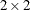 factorial layout, with two types of seeds, O. aegyptiaca 75 and O. aegyptiaca 73, and two root extracts, bean and cucumber. You observe
factorial layout, with two types of seeds, O. aegyptiaca 75 and O. aegyptiaca 73, and two root extracts, bean and cucumber. You observe r, which is the number of germinated seeds, and n, which is the total number of seeds. The independent variables are seed and extract.
The following statements create the data set:
title 'Logistic Regression Random-Effects Model'; data seeds; input r n seed extract @@; ind = _N_; datalines; 10 39 0 0 23 62 0 0 23 81 0 0 26 51 0 0 17 39 0 0 5 6 0 1 53 74 0 1 55 72 0 1 32 51 0 1 46 79 0 1 10 13 0 1 8 16 1 0 10 30 1 0 8 28 1 0 23 45 1 0 0 4 1 0 3 12 1 1 22 41 1 1 15 30 1 1 32 51 1 1 3 7 1 1 ;
You can model each observation  as having its own probability of success
as having its own probability of success 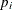 , and the likelihood is as follows:
, and the likelihood is as follows:
![\[ \mbox{r}_ i \sim \mbox{binomial}(\mbox{n}_ i, p_ i) \]](images/statug_mcmc0674.png)
You can use the logit link function to link the covariates of each observation, seed and extract, to the probability of success,
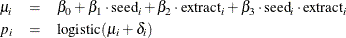
where 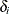 is assumed to be an iid random effect with a normal prior:
is assumed to be an iid random effect with a normal prior:
![\[ \delta _ i \sim \mbox{normal}(0, \mbox{var} = \sigma ^2) \]](images/statug_mcmc0677.png)
The four 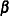 regression coefficients and the standard deviation
regression coefficients and the standard deviation 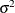 in the random effects are model parameters; they are given noninformative priors as follows:
in the random effects are model parameters; they are given noninformative priors as follows:
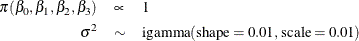
Another way of expressing the same model is as
![\[ p_ i = \mbox{logistic} ( \delta _ i ) \]](images/statug_mcmc0679.png)
where
![\[ \delta _ i \sim \mbox{normal}(\beta _0 + \beta _1 \cdot \mbox{seed}_ i + \beta _2 \cdot \mbox{extract}_ i + \beta _3 \cdot \mbox{seed}_ i \cdot \mbox{extract}_ i, \sigma ^2) \]](images/statug_mcmc0680.png)
The two models are equivalent. In the first model, the random effects 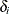 centers at 0 in the normal distribution, and in the second model,
centers at 0 in the normal distribution, and in the second model, 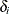 centers at the regression mean. This hierarchical centering can sometimes improve mixing.
centers at the regression mean. This hierarchical centering can sometimes improve mixing.
The following statements fit the second model and generate Output 73.7.1:
proc mcmc data=seeds outpost=postout seed=332786 nmc=20000; ods select PostSumInt; parms beta0 0 beta1 0 beta2 0 beta3 0 s2 1; prior s2 ~ igamma(0.01, s=0.01); prior beta: ~ general(0); w = beta0 + beta1*seed + beta2*extract + beta3*seed*extract; random delta ~ normal(w, var=s2) subject=ind; pi = logistic(delta); model r ~ binomial(n = n, p = pi); run;
The PROC MCMC statement specifies the input and output data sets, sets a seed for the random number generator, and requests
a large simulation size. The ODS SELECT statement displays the summary statistics and interval statistics tables. The PARMS
statement declares the model parameters, and the PRIOR
statements specify the prior distributions for 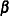 and
and 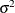 .
.
The symbol w calculates the regression mean, and the RANDOM
statement specifies the random effect, with a normal prior distribution, centered at w with variance 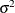 . Note that the variable
. Note that the variable w is a function of the input data set variables. You can use data set variable in constructing the hyperparameters of the random-effects
parameters, as long as the hyperparameters remain constant within each subject group. The SUBJECT=
option indicates the group index for the random-effects parameters.
The symbol pi is the logit transformation. The MODEL
specifies the response variable r as a binomial distribution with parameters n and pi.
Output 73.7.1 lists the posterior mean and interval estimates of the regression parameters.
Output 73.7.1: Logistic Regression Random-Effects Model
| Logistic Regression Random-Effects Model |
| Posterior Summaries and Intervals | |||||
|---|---|---|---|---|---|
| Parameter | N | Mean | Standard Deviation |
95% HPD Interval | |
| beta0 | 20000 | -0.5570 | 0.1929 | -0.9422 | -0.1816 |
| beta1 | 20000 | 0.0776 | 0.3276 | -0.5690 | 0.7499 |
| beta2 | 20000 | 1.3667 | 0.2923 | 0.8463 | 1.9724 |
| beta3 | 20000 | -0.8469 | 0.4718 | -1.7741 | 0.0742 |
| s2 | 20000 | 0.1171 | 0.0993 | 0.00163 | 0.3045 |