The MCMC Procedure

Example 73.9 Multivariate Normal Random-Effects Model

Gelfand et al. (1990) use a multivariate normal hierarchical model to estimate growth regression coefficients for the growth of 30 young rats in a control group over a period of 5 weeks. The following statements create a SAS data set with measurements of Weight, Age (in days), and Subject.

title 'Multivariate Normal Random-Effects Model';
data rats;
   array days[5] (8 15 22 29 36);
   input weight @@;
   subject = ceil(_n_/5);
   index = mod(_n_-1, 5) + 1;
   age = days[index];
   drop index days:;
   datalines;
151 199 246 283 320 145 199 249 293 354
147 214 263 312 328 155 200 237 272 297
135 188 230 280 323 159 210 252 298 331
141 189 231 275 305 159 201 248 297 338
177 236 285 350 376 134 182 220 260 296
160 208 261 313 352 143 188 220 273 314
154 200 244 289 325 171 221 270 326 358
163 216 242 281 312 160 207 248 288 324
142 187 234 280 316 156 203 243 283 317
157 212 259 307 336 152 203 246 286 321
154 205 253 298 334 139 190 225 267 302
146 191 229 272 302 157 211 250 285 323
132 185 237 286 331 160 207 257 303 345
169 216 261 295 333 157 205 248 289 316
137 180 219 258 291 153 200 244 286 324
;

The model assumes normal measurement errors,

$\mbox{Weight}_{ij} \sim \mbox{normal} \left( \alpha _ i + \beta _ i \mbox{Age}_{ij}, \sigma ^2 \right), ~ ~ ~ i = 1, \ldots , 30; j = 1, \ldots , 5$

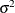where i indexes rat (Subject variable), j indexes the time period, Weight $_{ij}$ and Age $_{ij}$ denote the weight and age of the ith rat in week j, and $\sigma ^2$ is the variance in the normal likelihood. The individual intercept and slope coefficients are modeled as the following:

$\bm {\theta }_ i = \left(\begin{matrix} \alpha _ i \\ \beta _ i \end{matrix} \right) \sim \mbox{MVN} \left( \bm {\theta }_ c = \begin{pmatrix} \alpha _ c \\ \beta _ c \end{pmatrix}, \bm {\Sigma }_ c \right), ~ ~ ~ i = 1, \ldots , 30$

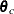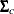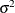You can use the following independent prior distributions on $\bm {\theta }_ c$ , $\bm {\Sigma }_ c$ , and $\sigma ^2$ :

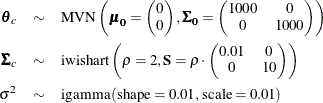
$\begin{eqnarray*} \bm {\theta }_ c & \sim & \mbox{MVN} \left( \bm {\mu _0} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} , \bm {\Sigma _0} = \begin{pmatrix} 1000 & 0 \\ 0 & 1000 \end{pmatrix} \right) \\ \bm {\Sigma }_ c & \sim & \mbox{iwishart} \left( \rho =2, \mb{S} = \rho \cdot \left( \begin{matrix} 0.01 & 0 \\ 0 & 10 \end{matrix} \right) \right) \\ \sigma ^2 & \sim & \mbox{igamma} \left( \mbox{shape}=0.01, \mbox{scale} = 0.01 \right) \end{eqnarray*}$

The following statements fit this multivariate normal random-effects model:

proc mcmc data=rats nmc=10000 outpost=postout
   seed=17 init=random;
   ods select Parameters REParameters PostSumInt;
   array theta[2] alpha beta;
   array theta_c[2];
   array Sig_c[2,2];
   array mu0[2] (0 0);
   array Sig0[2,2] (1000 0 0 1000);
   array S[2,2] (0.02 0 0 20);

   parms theta_c Sig_c {121 0 0 0.26} var_y;
   prior theta_c ~ mvn(mu0, Sig0);
   prior Sig_c ~ iwish(2, S);
   prior var_y ~ igamma(0.01, scale=0.01);

   random theta ~ mvn(theta_c, Sig_c) subject=subject
      monitor=(alpha_9 beta_9 alpha_25 beta_25);
   mu = alpha + beta * age;
   model weight ~ normal(mu, var=var_y);
run;

The ODS SELECT statement displays information about model parameters, random-effects parameters, and the posterior summary statistics. The ARRAY statements allocate memory space for the multivariate parameters and hyperparameters in the model. The parameters are 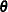$\bm {\theta }$ (theta where the variable name of each element is alpha or beta), 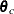$\bm {\theta }_ c$ (theta_c), and 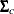$\bm {\Sigma }_ c$ (Sig_c). The hyperparameters are 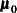$\bm {\mu _0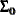}$ (mu0), $\bm {\Sigma _0}$ (Sig0), and 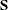$\bS$ (S). The multivariate hyperparameters are assigned with constant values using parentheses $( ~ ~ )$ .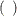

The PARMS statement declares model parameters and assigns initial values to Sig_c using braces 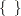$\{ ~ ~ \}$ . The PRIOR statements specify the prior distributions. The RANDOM statement defines an array random effect theta and specifies a multivariate normal prior distribution. The SUBJECT= option indicates cluster membership for each of the random-effects parameter. The MONITOR= option monitors the individual intercept and slope coefficients of subjects 9 and 25.

You can use the following syntax in the RANDOM statement to monitor all parameters in an array random effect:

monitor=(theta)

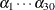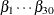This would produce posterior summary statistics on $\alpha _1 \cdots \alpha _{30}$ and $\beta _1 \cdots \beta _{30}$ .

The following syntax monitors all 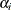$\alpha _ i$ parameters:

monitor=(alpha)

If you did not name elements of theta to be alpha and beta, the SAS System creates variable names automatically in a consecutive fashion, as in theta1 and theta2.

Output 73.9.1: Parameter and Random-Effects Parameter Information Table

Multivariate Normal Random-Effects Model

The MCMC Procedure

Parameters
Block	Parameter	Array Index	Sampling Method	Initial Value	Prior Distribution
1	theta_c1		Conjugate	-4.5834	MVNormal(mu0, Sig0)
	theta_c2			5.7930
2	Sig_c1	[1,1]	Conjugate	121.0	iWishart(2, S)
	Sig_c2	[1,2]		0
	Sig_c3	[2,1]		0
	Sig_c4	[2,2]		0.2600
3	var_y		Conjugate	2806714	igamma(0.01, scale=0.01)

Random Effect Parameters
Parameter	Sampling Method	Subject	Number of Subjects	Subject Values	Prior Distribution
theta	N-Metropolis	subject	30	1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 ...	MVNormal(theta_c, Sig_c)

Output 73.9.1 displays the parameter and random-effects parameter information tables. The Array Index column in "Parameters" table shows the index reference of the elements in the array parameter Sig_c. The total number of subjects in the study is 30.

Output 73.9.2: Multivariate Normal Random-Effects Model

Multivariate Normal Random-Effects Model

The MCMC Procedure

Posterior Summaries and Intervals
Parameter	N	Mean	Standard Deviation	95% HPD Interval
theta_c1	10000	106.1	2.2486	101.7	110.6
theta_c2	10000	6.1975	0.1988	5.8058	6.5815
Sig_c1	10000	110.8	45.9169	37.9670	203.8
Sig_c2	10000	-1.4267	2.3320	-6.2878	2.7756
Sig_c3	10000	-1.4267	2.3320	-6.2878	2.7756
Sig_c4	10000	1.0591	0.2979	0.5549	1.6538
var_y	10000	37.6855	5.9591	27.0943	49.4449
alpha_9	10000	119.4	5.6756	108.1	130.5
beta_9	10000	7.4670	0.2382	7.0146	7.9278
alpha_25	10000	86.5673	6.3694	74.4247	99.9007
beta_25	10000	6.7804	0.2612	6.2529	7.2906

Output 73.9.2 displays posterior summary statistics for model parameters and the random-effects parameters for subjects 9 and 25. You can see that there is a substantial difference in the intercepts and growth rates between the two rats.

A seemingly confusing message might occur if a symbol name matches an internally generated variable name for elements of an array. For example, if, instead of using the symbol var_y in the SAS program for the model variance 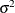$\sigma ^2$ , you used s2, the SAS System produces the following error message:

ERROR: The initial value 0 for the parameter S2 is outside of the prior
       distribution support set.

This is confusing because the program does not assign an initial value for the parameter s2 in the PARMS statement, and you might expect that PROC MCMC would not generate an invalid initial value. The confusion is caused by the ARRAY statement that defines the array variable S:

   array S[2,2] (0.02 0 0 20);

Elements of S are automatically given names s1–s4. PROC MCMC interprets s2 as an element in S that was given a value of 0, hence producing this error message.