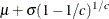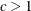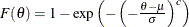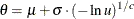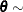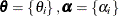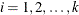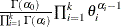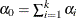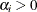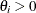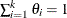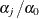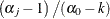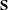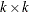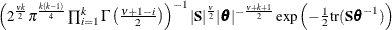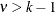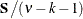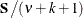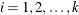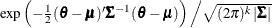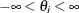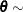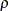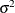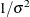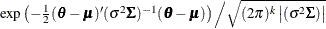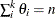The MCMC Procedure
-
Overview

-
Getting Started

-
Syntax

-
Details
 How PROC MCMC WorksBlocking of ParametersSampling MethodsTuning the Proposal DistributionDirect SamplingConjugate SamplingInitial Values of the Markov ChainsAssignments of ParametersStandard DistributionsUsage of Multivariate DistributionsSpecifying a New DistributionUsing Density Functions in the Programming StatementsTruncation and CensoringSome Useful SAS FunctionsMatrix Functions in PROC MCMCCreate Design MatrixModeling Joint LikelihoodAccess Lag and Lead VariablesCALL ODE and CALL QUAD SubroutinesRegenerating Diagnostics PlotsCaterpillar PlotAutocall Macros for PostprocessingGamma and Inverse-Gamma DistributionsPosterior Predictive DistributionHandling of Missing DataFunctions of Random-Effects ParametersFloating Point Errors and OverflowsHandling Error MessagesComputational ResourcesDisplayed OutputODS Table NamesODS Graphics
How PROC MCMC WorksBlocking of ParametersSampling MethodsTuning the Proposal DistributionDirect SamplingConjugate SamplingInitial Values of the Markov ChainsAssignments of ParametersStandard DistributionsUsage of Multivariate DistributionsSpecifying a New DistributionUsing Density Functions in the Programming StatementsTruncation and CensoringSome Useful SAS FunctionsMatrix Functions in PROC MCMCCreate Design MatrixModeling Joint LikelihoodAccess Lag and Lead VariablesCALL ODE and CALL QUAD SubroutinesRegenerating Diagnostics PlotsCaterpillar PlotAutocall Macros for PostprocessingGamma and Inverse-Gamma DistributionsPosterior Predictive DistributionHandling of Missing DataFunctions of Random-Effects ParametersFloating Point Errors and OverflowsHandling Error MessagesComputational ResourcesDisplayed OutputODS Table NamesODS Graphics -
Examples
 Simulating Samples From a Known DensityBox-Cox TransformationLogistic Regression Model with a Diffuse PriorLogistic Regression Model with Jeffreys’ PriorPoisson RegressionNonlinear Poisson Regression ModelsLogistic Regression Random-Effects ModelNonlinear Poisson Regression Multilevel Random-Effects ModelMultivariate Normal Random-Effects ModelMissing at Random AnalysisNonignorably Missing Data (MNAR) AnalysisChange Point ModelsExponential and Weibull Survival AnalysisTime Independent Cox ModelTime Dependent Cox ModelPiecewise Exponential Frailty ModelNormal Regression with Interval CensoringConstrained AnalysisImplement a New Sampling AlgorithmUsing a Transformation to Improve MixingGelman-Rubin DiagnosticsOne-Compartment Model with Pharmacokinetic Data
Simulating Samples From a Known DensityBox-Cox TransformationLogistic Regression Model with a Diffuse PriorLogistic Regression Model with Jeffreys’ PriorPoisson RegressionNonlinear Poisson Regression ModelsLogistic Regression Random-Effects ModelNonlinear Poisson Regression Multilevel Random-Effects ModelMultivariate Normal Random-Effects ModelMissing at Random AnalysisNonignorably Missing Data (MNAR) AnalysisChange Point ModelsExponential and Weibull Survival AnalysisTime Independent Cox ModelTime Dependent Cox ModelPiecewise Exponential Frailty ModelNormal Regression with Interval CensoringConstrained AnalysisImplement a New Sampling AlgorithmUsing a Transformation to Improve MixingGelman-Rubin DiagnosticsOne-Compartment Model with Pharmacokinetic Data - References
Standard Distributions
The section Univariate Distributions (Table 73.7 through Table 73.35) lists all univariate distributions that PROC MCMC recognizes. The section Multivariate Distributions (Table 73.36 through Table 73.40) lists all multivariate distributions that PROC MCMC recognizes. With the exception of the multinomial distribution, all these distributions can be used in the MODEL , PRIOR , and HYPERPRIOR statements. The multinomial distribution is supported only in the MODEL statement. The RANDOM statement supports a limited number of distributions; see Table 73.4 for the complete list.
See the section Using Density Functions in the Programming Statements for information about how to use distributions in the programming statements. To specify an arbitrary distribution, you can use the GENERAL and DGENERAL functions. See the section Specifying a New Distribution for more details. See the section Truncation and Censoring for tips about how to work with truncated distributions and censoring data.
Univariate Distributions
Table 73.7: Beta Distribution
Table 73.8: Binary Distribution
|
PROC specification |
binary(p) |
|
Density |
|
|
Parameter restriction |
|
|
Range |
|
|
Mean |
round |
|
Variance |
|
|
Mode |
|
|
Random number |
Generate |
Table 73.9: Binomial Distribution
|
PROC specification |
binomial(n, p) |
|
Density |
|
|
Parameter restriction |
|
|
Range |
|
|
Mean |
|
|
Variance |
|
|
Mode |
|
Table 73.10: Cauchy Distribution
|
PROC specification |
cauchy(a, b) |
|
Density |
|
|
Parameter restriction |
|
|
Range |
|
|
Mean |
Does not exist. |
|
Variance |
Does not exist. |
|
Mode |
a |
|
Random number |
Generate |
Table 73.11: 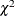 Distribution
Distribution
|
PROC specification |
chisq( |
|
Density |
|
|
Parameter restriction |
|
|
Range |
|
|
Mean |
|
|
Variance |
|
|
Mode |
|
|
Random number |
|
Table 73.12: Exponential 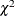 Distribution
Distribution
|
PROC specification |
expchisq( |
|
Density |
|
|
Parameter restriction |
|
|
Range |
|
|
Mode |
|
|
Random number |
Generate |
|
Relationship to the |
|
Table 73.13: Exponential Exponential Distribution
|
PROC specification |
expexpon( |
expexpon( |
|
Density |
|
|
|
Parameter restriction |
|
|
|
Range |
|
Same |
|
Mode |
|
|
|
Random number |
Generate |
|
|
Relationship to the exponential distribution |
|
|
Table 73.14: Exponential Gamma Distribution
|
PROC specification |
expgamma(a, |
expgamma(a, |
|
Density |
|
|
|
Parameter restriction |
|
|
|
Range |
|
Same |
|
Mode |
|
|
|
Random number |
Generate |
|
|
Relationship to the |
|
|
Table 73.15: Exponential Inverse 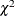 Distribution
Distribution
|
PROC specification |
expichisq( |
|
Density |
|
|
Parameter restriction |
|
|
Range |
|
|
Mode |
|
|
Random number |
Generate |
|
Relationship to the |
|
Table 73.16: Exponential Inverse-Gamma Distribution
|
PROC specification |
expigamma(a, |
expigamma(a, |
|
Density |
|
|
|
Parameter restriction |
|
|
|
Range |
|
Same |
|
Mode |
|
|
|
Random number |
Generate |
|
|
Relationship to the |
|
|
Table 73.17: Exponential Scaled Inverse 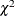 Distribution
Distribution
|
PROC specification |
expsichisq( |
|
Density |
|
|
Parameter restriction |
|
|
Range |
|
|
Mode |
|
|
Random number |
Generate |
|
Relationship to the |
|
Table 73.18: Exponential Distribution
|
PROC specification |
expon( |
expon( |
|
Density |
|
|
|
Parameter restriction |
|
|
|
Range |
|
Same |
|
Mean |
b |
|
|
Variance |
|
|
|
Mode |
0 |
0 |
|
Random number |
The exponential distribution is a special case of the gamma distribution: |
|
Table 73.19: Gamma Distribution
|
PROC specification |
gamma(a, |
gamma(a, |
|
Density |
|
|
|
Parameter restriction |
|
|
|
Range |
|
Same |
|
Mean |
ab |
|
|
Variance |
|
|
|
Mode |
|
|
|
Random number |
See (McGrath and Irving 1973). |
|
Table 73.20: Geometric Distribution
|
PROC specification |
geo(p) |
|
Density * |
|
|
Parameter restriction |
|
|
Range |
|
|
Mean |
round( |
|
Variance |
|
|
Mode |
0 |
|
Random number |
Based on samples obtained from a Bernoulli distribution with probability p until the first success. |
|
*The random variable |
|
Table 73.21: Inverse 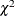 Distribution
Distribution
|
PROC specification |
ichisq( |
|
Density |
|
|
Parameter restriction |
|
|
Range |
|
|
Mean |
|
|
Variance |
|
|
Mode |
|
|
Random number |
Inverse |
Table 73.22: Inverse-Gamma Distribution
|
PROC specification |
igamma(a, |
igamma(a, |
|
Density |
|
|
|
Parameter restriction |
|
|
|
Range |
|
Same |
|
Mean |
|
|
|
Variance |
|
|
|
Mode |
|
|
|
Random number |
Generate |
|
|
Relationship to the gamma distribution |
|
|
Table 73.23: Laplace (Double Exponential) Distribution
|
PROC specification |
laplace(a, |
laplace(a, |
|
Density |
|
|
|
Parameter restriction |
|
|
|
Range |
|
Same |
|
Mean |
a |
a |
|
Variance |
|
|
|
Mode |
a |
a |
|
Random number |
Inverse CDF. |
|
Table 73.24: Logistic Distribution
|
PROC specification |
logistic(a, b) |
|
Density |
|
|
Parameter restriction |
|
|
Range |
|
|
Mean |
a |
|
Variance |
|
|
Mode |
a |
|
Random number |
Inverse CDF method with |
Table 73.25: Lognormal Distribution
|
PROC specification |
lognormal( |
lognormal( |
lognormal( |
|
Density |
|
|
|
|
Parameter restriction |
|
|
|
|
Range |
|
Same |
Same |
|
Mean |
|
|
|
|
Variance |
|
|
|
|
Mode |
|
|
|
|
Random number |
Generate |
||
Table 73.26: Negative Binomial Distribution
|
PROC specification |
negbin(n, p) |
|
Density |
|
|
Parameter restriction |
|
|
Range |
|
|
Mean |
round |
|
Variance |
|
|
Mode |
|
|
Random number |
Generate |
Table 73.27: Normal Distribution
|
PROC specification |
normal( |
normal( |
normal( |
|
Density |
|
|
|
|
Parameter restriction |
|
|
|
|
Range |
|
Same |
Same |
|
Mean |
|
Same |
Same |
|
Variance |
|
v |
|
|
Mode |
|
Same |
Same |
Table 73.28: Pareto Distribution
|
PROC specification |
pareto(a, b) |
|
Density |
|
|
Parameter restriction |
|
|
Range |
|
|
Mean |
|
|
Variance |
|
|
Mode |
b |
|
Random number |
Inverse CDF method with |
|
Useful transformation |
|
Table 73.29: Poisson Distribution
|
PROC specification |
poisson( |
|
Density |
|
|
Parameter restriction |
|
|
Range |
|
|
Mean |
|
|
Variance |
|
|
Mode |
round |
Table 73.30: Scaled Inverse 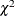 Distribution
Distribution
|
PROC specification |
sichisq( |
|
Density |
|
|
Parameter restriction |
|
|
Range |
|
|
Mean |
|
|
Variance |
|
|
Mode |
|
|
Random number |
Scaled inverse |
Table 73.31: t Distribution
|
PROC specification |
t( |
t( |
t( |
|
Density |
|
|
|
|
Parm restriction |
|
|
|
|
Range |
|
Same |
Same |
|
Mean |
|
Same |
Same |
|
Variance |
|
|
|
|
Mode |
|
Same |
Same |
|
Random number |
|
||
Table 73.32: Table (Categorical) Distribution
|
PROC specification |
table( |
|
Density |
|
|
Parameter restriction |
|
|
Range |
|
|
Mode |
i such that |
|
Random number |
Inverse CDF method with |
Table 73.33: Uniform Distribution
Table 73.34: Wald Distribution
|
PROC specification |
wald( |
|
Density |
|
|
Parameter restriction |
|
|
Range |
|
|
Mean |
|
|
Variance |
|
|
Mode |
|
|
Random number |
Generate |
Table 73.35: Weibull Distribution
|
PROC specification |
weibull( |
|
Density |
|
|
Parameter restriction |
|
|
Range |
|
|
Mean |
|
|
Variance |
|
|
Mode |
|
|
Random number |
Inverse CDF method with |
Multivariate Distributions
Table 73.36: Dirichlet Distribution
|
PROC specification |
|
|
Density |
|
|
Parameter restriction |
|
|
Range |
|
|
Mean |
|
|
Mode |
|
Table 73.37: Inverse Wishart Distribution
|
PROC specification |
|
|
Density |
|
|
Parameter restriction |
|
|
Range |
|
|
Mean |
|
|
Mode |
|
Table 73.38: Multivariate Normal Distribution
|
PROC specification |
|
|
Density |
|
|
Parameter restriction |
|
|
Range |
|
|
Mean |
|
|
Mode |
|
Table 73.39: Autoregressive Multivariate Normal Distribution
|
PROC specification |
|
|
|
|
Density |
![\[ \bSigma = \left[ \begin{array}{cccccc} 1 & \rho & \rho ^2 & \rho ^3 & \cdots & \rho ^ k \\ \rho & 1 & \rho & \rho ^2 & \cdots & \rho ^{k-1} \\ \rho ^2 & \rho & 1 & \rho & \cdots & \rho ^{k-2} \\ \rho ^3 & \rho ^2 & \rho & 1 & \cdots & \rho ^{k-3} \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ \rho ^ k & \rho ^{k-1} & \rho ^{k-2} & \rho ^{k-3} & \cdots & 1 \\ \end{array} \right] \]](images/statug_mcmc0456.png)
|
||
|
Parameter restriction |
|
||
|
Range |
|
||
|
Mean |
|
||
|
Mode |
|
||
|
Special Case |
When |
||
Table 73.40: Multinomial Distribution
|
PROC specification |
|
|
Density |
|
|
Parameter restriction |
|
|
Range |
|
|
Mean |
|
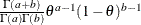
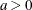
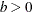
![$ \left\{ \begin{array}{ll} \left[ 0, 1 \right] & \mbox{when } a = 1, b = 1 \\ \left[ 0, 1 \right) & \mbox{when } a = 1, b \neq 1 \\ \left( 0, 1 \right] & \mbox{when } a \neq 1, b = 1 \\ \left( 0, 1 \right) & \mbox{otherwise} \end{array} \right. $](images/statug_mcmc0200.png)
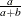
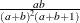
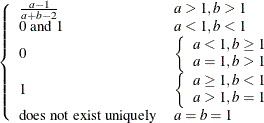
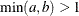
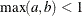
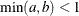
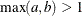
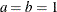
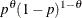
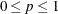
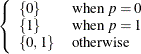
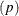
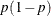
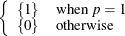
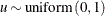
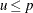
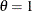
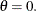
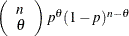
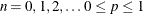
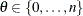
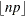
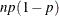
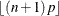
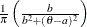
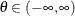
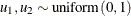
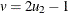
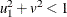
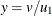
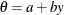

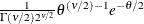
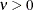
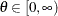
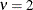
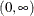

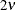
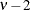
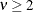
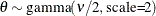
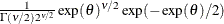
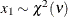
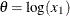
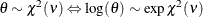
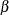
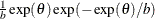
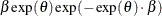
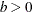
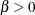
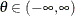
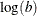
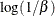
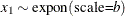
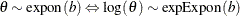
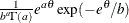
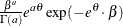
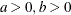
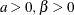
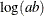
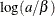
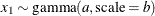

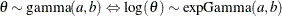
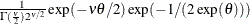
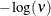
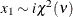
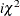
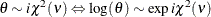
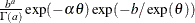
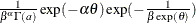
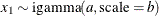
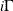
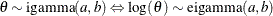
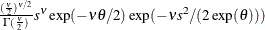
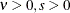
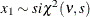
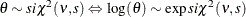
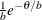
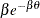
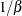
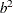
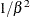
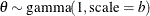
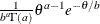
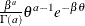
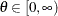
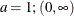
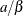
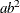
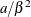
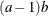
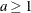
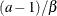
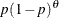
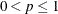
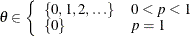
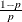
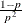
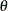
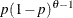
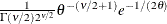
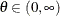
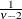
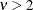
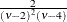
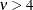
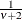
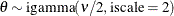
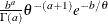
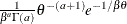
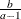
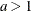
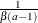
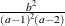
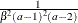
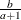
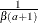
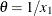
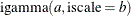
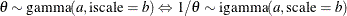
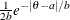
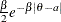
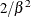
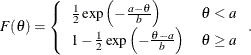
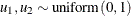
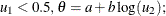
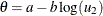
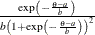
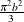
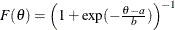
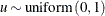
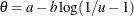
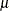

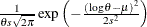
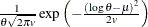
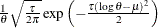
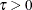
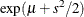
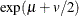
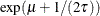
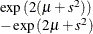
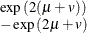
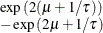
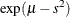
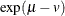
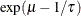

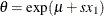
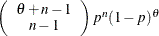
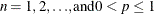
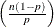
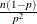
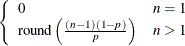
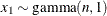
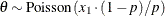
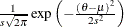
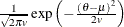
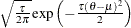
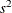
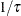
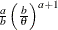
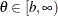
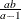
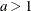
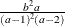
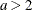
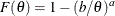
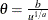
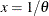
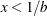
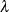
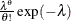
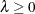
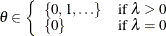
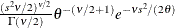
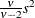
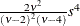
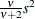
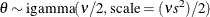
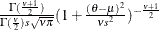
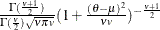
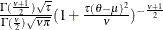
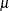
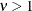
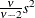
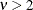
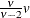
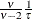
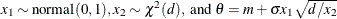
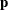
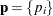
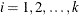
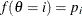
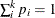
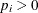
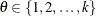
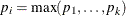
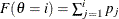
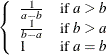
![$ \theta \in [a, b] $](images/statug_mcmc0408.png)
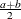
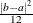
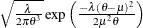
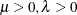
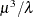
![$ \mu \left[ \left( 1 + \frac{9\mu ^2}{4\lambda ^2}\right)^{1/2} - \frac{3\mu }{2\lambda } \right]$](images/statug_mcmc0414.png)
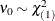
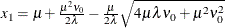
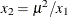
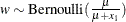
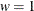
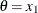
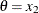

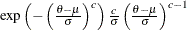
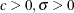
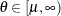
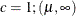
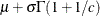
![$\sigma ^2 [\Gamma (1+2/c) - \Gamma ^2(1+1/c)]$](images/statug_mcmc0427.png)