The MCMC Procedure
-
Overview

-
Getting Started

-
Syntax

-
Details
 How PROC MCMC WorksBlocking of ParametersSampling MethodsTuning the Proposal DistributionDirect SamplingConjugate SamplingInitial Values of the Markov ChainsAssignments of ParametersStandard DistributionsUsage of Multivariate DistributionsSpecifying a New DistributionUsing Density Functions in the Programming StatementsTruncation and CensoringSome Useful SAS FunctionsMatrix Functions in PROC MCMCCreate Design MatrixModeling Joint LikelihoodAccess Lag and Lead VariablesCALL ODE and CALL QUAD SubroutinesRegenerating Diagnostics PlotsCaterpillar PlotAutocall Macros for PostprocessingGamma and Inverse-Gamma DistributionsPosterior Predictive DistributionHandling of Missing DataFunctions of Random-Effects ParametersFloating Point Errors and OverflowsHandling Error MessagesComputational ResourcesDisplayed OutputODS Table NamesODS Graphics
How PROC MCMC WorksBlocking of ParametersSampling MethodsTuning the Proposal DistributionDirect SamplingConjugate SamplingInitial Values of the Markov ChainsAssignments of ParametersStandard DistributionsUsage of Multivariate DistributionsSpecifying a New DistributionUsing Density Functions in the Programming StatementsTruncation and CensoringSome Useful SAS FunctionsMatrix Functions in PROC MCMCCreate Design MatrixModeling Joint LikelihoodAccess Lag and Lead VariablesCALL ODE and CALL QUAD SubroutinesRegenerating Diagnostics PlotsCaterpillar PlotAutocall Macros for PostprocessingGamma and Inverse-Gamma DistributionsPosterior Predictive DistributionHandling of Missing DataFunctions of Random-Effects ParametersFloating Point Errors and OverflowsHandling Error MessagesComputational ResourcesDisplayed OutputODS Table NamesODS Graphics -
Examples
 Simulating Samples From a Known DensityBox-Cox TransformationLogistic Regression Model with a Diffuse PriorLogistic Regression Model with Jeffreys’ PriorPoisson RegressionNonlinear Poisson Regression ModelsLogistic Regression Random-Effects ModelNonlinear Poisson Regression Multilevel Random-Effects ModelMultivariate Normal Random-Effects ModelMissing at Random AnalysisNonignorably Missing Data (MNAR) AnalysisChange Point ModelsExponential and Weibull Survival AnalysisTime Independent Cox ModelTime Dependent Cox ModelPiecewise Exponential Frailty ModelNormal Regression with Interval CensoringConstrained AnalysisImplement a New Sampling AlgorithmUsing a Transformation to Improve MixingGelman-Rubin DiagnosticsOne-Compartment Model with Pharmacokinetic Data
Simulating Samples From a Known DensityBox-Cox TransformationLogistic Regression Model with a Diffuse PriorLogistic Regression Model with Jeffreys’ PriorPoisson RegressionNonlinear Poisson Regression ModelsLogistic Regression Random-Effects ModelNonlinear Poisson Regression Multilevel Random-Effects ModelMultivariate Normal Random-Effects ModelMissing at Random AnalysisNonignorably Missing Data (MNAR) AnalysisChange Point ModelsExponential and Weibull Survival AnalysisTime Independent Cox ModelTime Dependent Cox ModelPiecewise Exponential Frailty ModelNormal Regression with Interval CensoringConstrained AnalysisImplement a New Sampling AlgorithmUsing a Transformation to Improve MixingGelman-Rubin DiagnosticsOne-Compartment Model with Pharmacokinetic Data - References
Example 73.11 Nonignorably Missing Data (MNAR) Analysis
This example illustrates how to fit a nonignorably missing data model (MNAR) with PROC MCMC. For a short overview of missing data problems, see the section Handling of Missing Data.
This data set comes from an environmental study that involve workers in a cotton factory. A similar data set was analyzed from Ibrahim, Chen, and Lipsitz (2001). There are 912 workers in the data set, and the response variable of interest is whether they develop dyspnea (difficult or labored respiration). The data are collected over three time points, and there are six covariates. The following statements create the data set:
title 'Nonignorably Missing Data Analysis';
data dyspnea;
input smoke1 smoke2 smoke3 y1 y2 y3 yrswrk1 yrswrk2 yrswrk3
age expd sex hgt;
datalines;
0 0 0 0 0 0 28.1 33.1 39.1 48 1 1 165.0
0 0 0 0 . 0 5.1 10.1 16.1 45 1 0 147.0
0 0 0 0 . 0 26.0 31.0 37.0 46 1 0 156.0
... more lines ...
1 1 1 0 . . 6.0 11.0 17.0 25 0 1 180.0
0 0 0 0 . . 20.0 25.0 31.0 42 0 0 159.0
;
The following variables are included in the data set:
-
y1,y2, andy3: dichotomous outcome at the three time periods, which takes the value 1 if the worker has dyspnea, 0 if not (there are missing values iny2and y3) -
smoke1,smoke2,smoke3: smoking status (0=no, and 1=yes) -
yrswrk1,yrswrk2,yrswrk3: years worked at the cotton factory -
age: age of the worker -
expd: cotton dust exposure (0=no, 1=yes) -
sex: gender (0=female, 1=male) -
hgt: height of the worker
Prior to the analysis, three missing data indicator variables (r1, r2, and r3, one for each of the response variables) are created, and they are set to 1 if the response variable is missing, and 0 otherwise.
The covariates age, hgt, yrswrk1, yrswkr2, and yrswrk3 are standardized:
data dyspnea;
array y[3] y1-y3;
array r[3];
set dyspnea;
do i = 1 to 3;
if y[i] = . then r[i] = 1;
else r[i] = 0;
end;
output;
run;
proc standard data=dyspnea out=dyspnea mean=0 std=1;
var age hgt yrswrk:;
run;
There are no missing values in response variable y1, 128 missing values in y2, and 131 in y3. Ibrahim, Chen, and Lipsitz (2001) used a logistic regression for each of the response variables, where 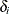 is a scalar random effect on the observational level:
is a scalar random effect on the observational level:
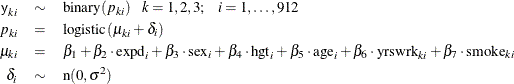
Ibrahim, Chen, and Lipsitz (2001) noted that taking 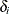 to be higher dimensional (3) would make the model either not identifiable or nearly not identifiable because of the multiple
missing values for some subjects.
to be higher dimensional (3) would make the model either not identifiable or nearly not identifiable because of the multiple
missing values for some subjects.
The first response variable y1 does not contain any missing values, making it meaningless to model the corresponding r1 because every value is 1. Hence, only r2 and r3 are considered in the missing mechanism part of the model. Ibrahim, Chen, and Lipsitz (2001) suggest the following logistic regression for r2 and r3, where the regression mean for each r depends not only on the current response variable y but also the response from previous time period:
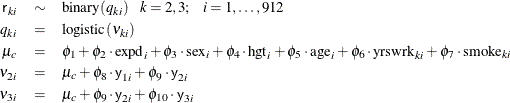
The missing mechanism model introduces an additional 10 parameters to the model. Normal priors with large standard deviations are used here.
The following statements fit a nonignorably missing model to the dyspnea data set:
ods select MissDataInfo REParameters Postsumint;
proc mcmc data=dyspnea seed=17 outpost=dysp2 nmc=20000
propcov=simplex diag=none monitor=(beta1-beta7);
array p[3];
array yrswrk[3];
array smoke[3];
parms beta1-beta7 s2;
parms phi1-phi10;
prior beta: phi: ~ n(0, var=1e6);
prior s2 ~ igamma(2, scale=2);
random d ~ n(0, var=s2) subject=_obs_;
mu = beta1 + beta2*expd + beta3*sex + beta4*hgt + beta5*age + d;
do j = 1 to 3;
p[j] = logistic(mu + beta6*yrswrk[j] + beta7*smoke[j]);
end;
model y1 ~ binary(p1);
model y2 ~ binary(p2);
model y3 ~ binary(p3);
nu = phi1 + phi2*expd + phi3*sex + phi4*hgt + phi5*age;
q2 = logistic(nu + phi6*yrswrk[2] + phi7*smoke[2] +
phi8*y1 + phi9*y2);
model r2 ~ binary(q2);
q3 = logistic(nu + phi6*yrswrk[3] + phi7*smoke[3] +
phi9*y2 + phi10*y3);
model r3 ~ binary(q3);
run;
The first ARRAY
statement declares an array p of size 3. This arrays stores three binary probabilities of the response variables. The next two ARRAY
statements create storage arrays for some of yrswrk and smoke variables for later programming convenience. The first PARMS
statement declares eight parameters, 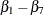 and
and 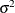 . The second PARMS
statement declares the 10
. The second PARMS
statement declares the 10  parameters for the missing mechanism model. The PRIOR
statements assign prior distributions to these parameters.
parameters for the missing mechanism model. The PRIOR
statements assign prior distributions to these parameters.
The RANDOM
statement defines an observational-level random effect d that has a normal prior with variance s2. The SUBJECT=_OBS_
option enables the specification of individual random effects without an explicit input data set variable.
The MU assignment statement and the following DO loop statements calculate the binary probabilities for the three response
variables. Note that different yrswrk and smoke variables are used in the DO loop for different years. The three MODEL
statements assign three binary distributions to the response variables.
The NU assignment statement starts the calculation for the regression mean in the logistic model for r2 and r3. The variables q2 and q3 are the binary probabilities for the missing mechanisms. Note that their calculations are conditional on the response variables
y (pattern mixture model). The last two MODEL
statements for r2 and r3 complete the specification of the models.
Missing data information and random-effects parameters information are displayed in Output 73.11.1. You can read the total number of missing observations from each variable and its indices from the table. The missing values are sampled using the inverse CDF method. There are 912 random-effects parameters in the model.
Output 73.11.1: Missing Data and Random-Effects Information
| Nonignorably Missing Data Analysis |
| Missing Data Information Table | |||
|---|---|---|---|
| Variable | Number of Missing Obs |
Observation Indices |
Sampling Method |
| y2 | 128 | 2 3 9 11 13 19 20 21 30 31 32 35 39 40 43 56 58 71 75 95 ... | Inverse CDF |
| y3 | 131 | 9 14 16 20 21 29 31 32 43 45 56 72 86 115 117 121 124 142 149 160 ... | Inverse CDF |
The posterior summary and interval statistics of all the 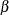 parameters are shown in Output 73.11.2. There are a number of significant regression coefficients in modeling the probability of a worker developing dyspnea, including
those for
parameters are shown in Output 73.11.2. There are a number of significant regression coefficients in modeling the probability of a worker developing dyspnea, including
those for expd (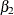 ),
), sex (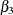 ),
), age (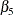 ), and
), and smoke (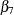 ).
).
Output 73.11.2: Posterior Summary Statistics for 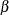
| Nonignorably Missing Data Analysis |
| Posterior Summaries and Intervals | |||||
|---|---|---|---|---|---|
| Parameter | N | Mean | Standard Deviation |
95% HPD Interval | |
| beta1 | 20000 | -2.3256 | 0.1771 | -2.6670 | -1.9826 |
| beta2 | 20000 | 0.5327 | 0.1530 | 0.2306 | 0.8193 |
| beta3 | 20000 | -0.5966 | 0.2593 | -1.0906 | -0.0691 |
| beta4 | 20000 | -0.0682 | 0.1061 | -0.2734 | 0.1462 |
| beta5 | 20000 | 0.6252 | 0.1640 | 0.2992 | 0.9490 |
| beta6 | 20000 | -0.1776 | 0.1574 | -0.4971 | 0.1218 |
| beta7 | 20000 | 0.5862 | 0.2214 | 0.1433 | 1.0051 |