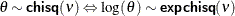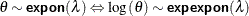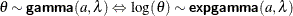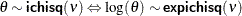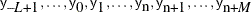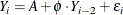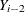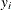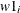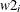The MCMC Procedure

MODEL Statement

Subsections:

Distributions in MODEL Statement
Options for the MODEL Statement

MODEL dependent-variable-list ~distribution <options>;

The MODEL statement specifies the conditional distribution of the data given the parameters (the likelihood function). You specify a single dependent variable or a list of dependent variables, a tilde ~, and then a distribution with its arguments. The dependent variables can be variables from the input data set or functions of the symbols in the program. You must specify the dependent variables unless you use the GENERAL function or the DGENERAL function (see the section Specifying a New Distribution for more details).

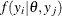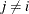The MODEL statement assumes that the observations are independent of each other, conditional on the model parameters. If you want to model dependent data—that is, $f(y_ i | \theta , y_ j)$ for $j \neq i$ —you can use the JOINTMODEL option in the PROC MCMC statement. See the section Modeling Joint Likelihood for more details. By default, the log-likelihood value is the sum of the individual log-likelihood value for each observation.

You can specify multiple MODEL statements. You can define likelihood functions that are independent of each other. For example, in the following statements, the dependent variables y1 and y2 are independent of each other:

model y1 ~ normal(alpha, var=s21);
model y2 ~ normal(beta,  var=s22);

Alternatively, you can use marginal and conditional distributions to define a joint log-likelihood function for multiple dependent variables. For example, the following statements jointly define a distribution over 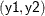$({\Variable{y1}}, {\Variable{y2}})$ . They specify a marginal distribution for the dependent variable y1 and a conditional distribution for the dependent variable y2:

model y1 ~ normal(alpha, var=s21);
model y2 ~ normal(beta * y1,  var=s22);

Every program must have at least one MODEL statement. If you want to run a Monte Carlo simulation that does not require a response variable, use the GENERAL function in the MODEL statement:

model general(0);

PROC MCMC interprets the statement as a flat likelihood function with a constant log-likelihood value of 0.

PROC MCMC is a programming language that is similar to the DATA step, and the order of statement evaluation is important. For example, the MODEL statement must come after any SAS programming statements that define or modify arguments used in the construction of the log likelihood. In PROC MCMC, a symbol can be defined multiple times and used at different places. Using an expression out of order produces erroneous results that can also be hard to detect.

Do not embed the MODEL statement within programming statements. For example, suppose you have three response variables, y1, y2, and y3, and want to model each with a normal distribution. The following statements lead to erroneous output:

array Y[3] y1 y2 y3;
do i = 1 to 3;
   model y[i] ~ normal(mu, sd=s);
end;

Instead, you should do one of the following.

Use separate MODEL statements:

model y1 ~ normal(mu, sd=s);
model y2 ~ normal(mu, sd=s);
model y3 ~ normal(mu, sd=s);

Use the GENERAL function to construct a joint distribution of the three dependent variables and use a single MODEL statement to specify the log-likelihood function:
```
llike = logpdf("normal", y1, mu, s) +
        logpdf("normal", y2, mu, s) +
        logpdf("normal", y3, mu, s);
model y1 y2 y3 ~ general(llike);
```
See the section Specifying a New Distribution for more information about how to use the GENERAL function to specify an arbitrary distribution.

Missing data are allowed in the response variables; the MODEL statement augments missing data automatically. (In releases before SAS/STAT 12.1, observations with missing values were discarded prior to analysis and PROC MCMC did not attempt to model these values.) In each iteration, PROC MCMC samples missing values from their posterior distributions and incorporates them as part of the simulation. PROC MCMC creates one variable for each missing response value. There are two ways to create the missing value variable names; see the NAMESUFFIX= option for the naming convention of the variables.

Distributions in MODEL Statement

Standard distributions that the MODEL statement supports are listed in the Table 73.2 (univariate) and Table 73.3 (multivariate). See the section Standard Distributions for density specifications. You can also specify all distributions except the multinomial distribution in the PRIOR and HYPERPRIOR statements. The RANDOM statement supports only a subset of the distributions (see Table 73.4).

PROC MCMC allows some distributions to be parameterized in multiple ways. For example, you can specify a normal distribution with a variance, standard deviation, or precision parameter. For distributions that have different parameterizations, you must specify an option to clearly name the ambiguous parameter. For example, in the normal distribution, you must indicate whether the second argument represents variance, standard deviation, or precision.

All univariate distributions, with the exception of binary and uniform, can have the optional LOWER= and UPPER= arguments, which specify a truncated density. See the section Truncation and Censoring for more details. Truncation is not supported for multivariate distributions.

Table 73.2: Univariate Distributions

Distribution Name	Definition
beta (<a=> $\alpha$ , <b=> $\beta$ )	Beta distribution with shape parameters $\alpha$ and $\beta$
binary (<prob\|p=> p)	Binary (Bernoulli) distribution with probability of success p. You can use the alias bern for this distribution.
binomial (<n=> n, <prob\|p=> p)	Binomial distribution with count n and probability of success p
cauchy (<location\|loc\|l=> $\theta$ , <scale\|s=> $\lambda$ )	Cauchy distribution with location $\theta$ and scale $\lambda$
chisq (<df=> $\nu$ )	$\chi ^2$ distribution with $\nu$ degrees of freedom
dgeneral (ll)	General log-likelihood function that you construct using SAS programming statements for single or multiple discrete parameters. Also see the function general. The name dlogden is an alias for this function.
expchisq (<df=> $\nu$ )	Log transformation of a $\chi ^2$ distribution with $\nu$ degrees of freedom: $\theta \sim {\Keyword{chisq}}(\nu ) \Leftrightarrow \log (\theta ) \sim {\Keyword{expchisq}}(\nu )$ . You can use the alias echisq for this distribution.
expexpon (scale\|s= $\lambda$ ) expexpon (iscale\|is= $\lambda$ )	Log transformation of an exponential distribution with scale or inverse-scale parameter $\lambda$ : $\theta \sim {\Keyword{expon}}(\lambda ) \Leftrightarrow \log (\theta ) \sim {\Keyword{expexpon}}(\lambda )$ . You can use the alias eexpon for this distribution.
expGamma (<shape\|sp=> a, scale\|s= $\lambda$ ) expGamma (<shape\|sp=> a, iscale\|is= $\lambda$ )	Log transformation of a gamma distribution with shape a and scale or inverse-scale $\lambda$ : $\theta \sim {\Keyword{gamma}}(a, \lambda ) \Leftrightarrow \log (\theta ) \sim {\Keyword{expgamma}}(a, \lambda )$ . You can use the alias egamma for this distribution.
expichisq (<df=> $\nu$ )	Log transformation of an inverse $\chi ^2$ distribution with $\nu$ degrees of freedom: $\theta \sim {\Keyword{ichisq}}(\nu ) \Leftrightarrow \log (\theta ) \sim {\Keyword{expichisq}}(\nu )$ . You can use the alias eichisq for this distribution.
expiGamma (<shape\|sp=> a, scale\|s= $\lambda$ ) expiGamma (<shape\|sp=> a, iscale\|is= $\lambda$ )	Log transformation of an inverse-gamma distribution with shape a and scale or inverse-scale $\lambda$ : $\theta \sim {\Keyword{igamma}}(a, \lambda ) \Leftrightarrow \log (\theta ) \sim {\Keyword{expigamma}}(a, \lambda )$ . You can use the alias eigamma for this distribution.
expsichisq (<df=> $\nu$ , <scale\|s=> s)	Log transformation of a scaled inverse $\chi ^2$ distribution with $\nu$ degrees of freedom and scale parameter s: $\theta \sim {\Keyword{sichisq}}(\nu ) \Leftrightarrow \log (\theta ) \sim {\Keyword{expsichisq}}(\nu )$ . You can use the alias esichisq for this distribution.
expon (scale\|s= $\lambda$ ) expon (iscale\|is= $\lambda$ )	Exponential distribution with scale or inverse-scale parameter $\lambda$
gamma (<shape\|sp=> a, scale\|s= $\lambda$ ) gamma (<shape\|sp=> a, iscale\|is= $\lambda$ )	Gamma distribution with shape a and scale or inverse-scale $\lambda$
geo (<prob\|p=> p)	Geometric distribution with probability p
general (ll)	General log-likelihood function that you construct using SAS programming statements for a single or multiple continuous parameters. The argument ll is an expression for the log of the distribution. If there are multiple variables specified before the tilde in a MODEL, PRIOR, or HYPERPRIOR statement, ll is interpreted as the log of the joint distribution for these variables. Note that in the MODEL statement, the response variable specified before the tilde is just a place holder and is of no consequence; the variable must have appeared in the construction of ll in the programming statements. general(constant) is equivalent to a uniform distribution on the real line. You can use the alias logden for this distribution.
ichisq (<df=> $\nu$ )	Inverse $\chi ^2$ distribution with $\nu$ degrees of freedom
igamma (<shape\|sp=> a, scale\|s= $\lambda$ ) igamma (<shape\|sp=> a, iscale\|is= $\lambda$ )	Inverse-gamma distribution with shape a and scale or inverse-scale $\lambda$
laplace (<location\|loc\|l=> $\theta$ , scale\|s= $\lambda$ ) laplace (<location\|loc\|l=> $\theta$ , iscale\|is= $\lambda$ )	Laplace distribution with location $\theta$ and scale or inverse-scale $\lambda$ . This is also known as the double exponential distribution. You can use the alias dexpon for this distribution.
logistic (<location\|loc\|l=> a, <scale\|s=> b)	Logistic distribution with location a and scale b
lognormal (<mean\|m=> $\mu$ , sd= $\lambda$ ) lognormal (<mean\|m=> $\mu$ , var\|v= $\lambda$ ) lognormal (<mean\|m=> $\mu$ , prec= $\lambda$ )	Log-normal distribution with mean $\mu$ and a value of $\lambda$ for the standard deviation, variance, or precision. You can use the aliases lognormal or lnorm for this distribution.
negbin (<n=> n, <prob\|p=> p)	Negative binomial distribution with count n and probability of success p. You can use the alias nb for this distribution.
normal (<mean\|m=> $\mu$ , sd= $\lambda$ ) normal (<mean\|m=> $\mu$ , var\|v= $\lambda$ ) normal (<mean\|m=> $\mu$ , prec= $\lambda$ )	Normal (Gaussian) distribution with mean $\mu$ and a value of $\lambda$ for the standard deviation, variance, or precision. You can use the aliases gaussian, norm, or n for this distribution.
pareto (<shape\|sp=> a, <scale\|s=> b)	Pareto distribution with shape a and scale b
poisson (<mean\|m=> $\lambda$ )	Poisson distribution with mean $\lambda$
sichisq (<df=> $\nu$ , <scale\|s=> s)	Scaled inverse $\chi ^2$ distribution with $\nu$ degrees of freedom and scale parameter s
t (<mean\|m=> $\mu$ , sd= $\lambda$ , <df=> $\nu$ ) t (<mean\|m=> $\mu$ , var\|v= $\lambda$ , <df=> $\nu$ ) t (<mean\|m=> $\mu$ , prec= $\lambda$ , <df=> $\nu$ )	T distribution with mean $\mu$ , standard deviation or variance or precision $\lambda$ , and $\nu$ degrees of freedom
table (<p=> p)	Table (categorical) distribution with probability vector p. You can also use the alias cat for this distribution.
uniform (<left\|l=> a, <right\|r=> b)	Uniform distribution with range a and b. You can use the alias unif for this distribution.
wald (<mean\|m=> $\mu$ , <iscale\|is=> $\lambda$ )	Wald distribution with mean parameter $\mu$ and inverse scale parameter $\lambda$ . This is also known as the Inverse Gaussian distribution. You can use the alias igaussian for this distribution.
weibull ( $\mu , c, \sigma$ )	Weibull distribution with location (threshold) parameter $\mu$ , shape parameter c, and scale parameter $\sigma$ .

Table 73.3: Multivariate Distributions

Distribution Name	Definition
dirichlet (<alpha=> $\alpha$ )	Dirichlet distribution with parameter vector $\alpha$ , where $\alpha$ must be a one-dimensional array of length greater than 1
iwish (<df=> $\nu$ , <scale=>S)	Inverse Wishart distribution with $\nu$ degrees of freedom and symmetric positive definite scale array S
multinom (<p=>p)	Multinomial distribution with probability vector p
mvn (<mu=> $\mu$ , <cov=> $\Sigma$ )	Multivariate normal distribution with mean vector $\mu$ and covariance matrix $\Sigma$
MVNAR (<mu=> $\mu$ , sd= $\lambda$ , <rho=> $\rho$ ) MVNAR (<mu=> $\mu$ , var= $\lambda$ , <rho=> $\rho$ ) MVNAR (<mu=> $\mu$ , prec= $\lambda$ , <rho=> $\rho$ )	Multivariate normal distribution with mean vector $\mu$ and a covariance matrix $\Sigma$ . The covariance matrix $\Sigma$ is a multiple of the scale and a matrix with a first-order autoregressive structure. When RHO=0, this distribution becomes a multivariate normal distribution with shared variance.

Options for the MODEL Statement

The options in the MODEL statement apply when there are missing values in the response variable, or in the case of the ICOND= option, when there are lag or lead variables for the response variable. You can specify the following options.

ICOND=variable-list | numeric-list

specifies the initial conditions (or initial states) of the lag or lead variables for the response variable when the observation indices are out of the range. (For more information about rules of constructing lag and lead variables in PROC MCMC, see the section Access Lag and Lead Variables.) For example, you can use the ICOND= option to specify the lag 1 value of the response for the first observation. This option works similarly to the ICOND= option in the RANDOM statement, except that the index is done according to observations, not a subject variable. The initial conditions can be model parameters, functions of model parameters, or constants. By default, numeric-list is set to 0.

The ICOND= option in a MODEL statement sets the initial conditions for all lag or lead variables (for the associated response variable) that appear in the program, not just those that appear in the MODEL statement. Suppose you have a maximum L number of lag variables and a maximum M number of lead variables of the response y in the program, and there are n observations. The program has the following variables that need to be resolved during the simulation:

$\begin{equation*} \Variable{y}_{\mbox{--\emph{L}+1}}, \ldots ,\Variable{y}_{\mbox{0}}, \Variable{y}_{\mbox{1}}, \ldots , \Variable{y}_{\mbox{n}}, \Variable{y}_{\mbox{n+1}}, \ldots , \Variable{y}_{\mbox{n+\emph{M}}} \end{equation*}$

Of these variables, n are observations of y from the input data set and the remaining L+M are initial conditions that are specified in the ICOND= option. In essence, the ICOND= numeric list stretches the input data set by filling in the first L and last M values. As PROC MCMC steps through the input data set, it resolves the current, lagged, and lead variables according to this stretched vector of observations.

The variable-list (or the number-list) should be of length L+M, which can be greater than the number of lag or lead response variables that appear in a program. Here is an example.

Suppose you want to fit an autoregressive model of order 2. And instead of two lagged values, the model requires only the second lag,

$\begin{equation*} Y_ i = A + \phi \cdot Y_{i-2} + \epsilon _ i \end{equation*}$

where the noise is assumed to be normal. To specify this autoregressive model, you would use the statements

mu = A + phi * y.l2;
model y ~ normal(mu, var=s2) icond=(-2 -1);

where the $Y_{i-2}$ , or the lag-2 of Y, variable is constructed by concatenating the variable name, the letter L (for “lag”), and a lag number.

This model requires two initial conditions for the lag-2 variable of Y, at the first and second observations. Therefore, the ICOND= option expects a numeric list of two values. In this example, at the first observation, the variable y.l2 is given a value of –2; at the second observation, y.l2 is given a value of –1. If you provide a partial list that contains less than the expected number of conditions, PROC MCMC fills the remaining list with the value of 0.

INITIAL=SAS-data-set | constant | numeric-list

specifies the initial values of the missing values. By default, PROC MCMC uses a sample average of the nonmissing values of a response variable as the starting values for all missing values in the simulation for that variable. You can use the INITIAL= option to start the Markov chain at a different place.

If you use a SAS-data-set to store initial values, the data set must consist of variable names that agree with the missing variable names that are used by PROC MCMC. The easiest way to find the names of the internally created variables is to run a default analysis with a very small number of simulations and check the variable names in the OUTPOST= data set. You can provide a subset of the initial values in the SAS-data-set, and PROC MCMC uses a default mechanism to fill in the rest of the missing initial values.

For example, the following statement creates a data set with initial values for the first three missing values of a response variable:

data RandomInit;
   input y_1 y_2 y_3;
   datalines;
2.3 3 -3
;

The following MODEL statement uses the values in the RandomInit data set as the initial values of the corresponding missing values in the model:

model y ~ normal(0,var=s2u) init=randominit;

Specifying a constant assigns that constant as the initial value to all missing values in that response variable. For example, the following statement assigns the value 5 to be used as an initial value for all missing $y_ i$ in the model:

model y ~ normal(0,var=s2u) init=5;

If you have a multidimensional response variable, you can provide a list of numbers that have the same length as the dimension of your response array. Each number is then given to all corresponding missing variables in order. For example, the following statement assigns the value 2 to be used as an initial value for all missing $w1_ i$ and the value 3 to be used for all missing $w2_ i$ in the model:

array w[2] w1 w2;
model w ~ mvn(mu, cov) init=(2 3);

MONITOR= (symbol-list | number-list | RANDOM(number))

outputs analysis for selected missing data variables. You can choose to monitor the missing values by listing the response variable names, the missing data variable names, or indices, or you can have them randomly selected by PROC MCMC.

For example, suppose that the data set contains 10 observations and the response variable y has missing values in observations 2, 3, 7, 9, and 10. To monitor all missing data variables (five in total), you specify the response variable name in the MONITOR= option:

model y ~ normal(0,var=s2u) monitor=(y);

Suppose you want to monitor the missing data variables that correspond to the missing values in observations 2, 3, and 10. You have two options: provide either a list of variable names or a list of indices.

The following statement selects monitored variables by their variable names:

model y ~ normal(0,var=s2u) monitor=(y_2 y_3 y_10);

The variable names must match the internally created variable names for each missing value. See NAMESUFFIX= option for the naming convention of the variables. By default, the names are created by concatenating the response variable with the observation index; hence you use the name_obs format to construct the names. The numbers 2, 3, and 10 are the corresponding observation indices to the missing values in the input data set.

The following statement selects monitored variables by indices:

model y ~ normal(0,var=s2u) monitor=(1 2 5);

The indices are not a list of the observation numbers, but rather the order by which the missing values appear in the data set: PROC MCMC reports back the first, the second, and the fifth missing value variables that it creates. The actual variable names that appear in the output are still y_2, y_3, and y_10, honoring the control of the NAMESUFFIX= option.

Lastly, PROC MCMC can randomly choose a subset of the variables to monitor. The following statement randomly selects 3 variables to monitor:

model y ~ normal(0,var=s2u) monitor=(random(3));

The list of the random indices is controlled by the SEED= option in the PROC MCMC statement. Therefore, the selected variables will be the same when the SEED= option is the same.

NAMESUFFIX=OBSERVATION | POSITION | ORDER

specifies how the names of the missing data variables are created. By default, the names are created by concatenating the response variable symbol, an underscore (“_”), and the observation number of the missing value.

NAMESUFFIX=OBSERVATION constructs the parameter names by appending the observation number to the response variable symbol. This is the default. NAMESUFFIX=POSITION or NAMESUFFIX=ORDER construct the parameter names by appending the numbers 1, 2, 3, and so on, where the number indicates the order in which the missing values appear in the data set.

For example, suppose you have a response variable y with 10 observations in total, of which five are missing (observations 2, 3, 7, 9, and 10). By default, PROC MCMC creates five variable names y_2, y_3, y_7, y_9, and y_10. Using NAMESUFFIX=POSITION changes the names to y_1, y_2, y_3, y_4, and y_5.

NOOUTPOST

suppresses the output of the posterior samples of missing data variables to the posterior output data set (which is specified in the OUTPOST= option in the PROC MCMC statement). In models with a large number of missing values (for example, tens of thousands), PROC MCMC can run faster if it does not save the posterior samples.

When you specify both the NOOUTPOST option and the MONITOR= option, PROC MCMC outputs the list of variables that are monitored.

The maximum number of variables that can be saved to an OUTPOST= data set is 32,767. If the total number of parameters in your model, including the number of missing data variables, exceeds the limit, the NOOUTPOST option is evoked automatically and PROC MCMC does not save the missing value draws to the posterior output data set. You can use the MONITOR= option to select a subset of the parameters to store in the OUTPOST= data set.