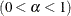The MCMC Procedure

Autocall Macros for Postprocessing

Although PROC MCMC provides a number of convergence diagnostic tests and posterior summary statistics, PROC MCMC performs the calculations only if you specify the options in advance. If you wish to analyze the posterior draws of unmonitored parameters or functions of the parameters that are calculated in later DATA step calls, you can use the autocall macros in Table 73.46.

Table 73.46: Postprocessing Autocall Macros

Macro	Description
%ESS	Effective sample sizes
%GEWEKE^*	Geweke diagnostic
%HEIDEL^*	Heidelberger-Welch diagnostic
%MCSE	Monte Carlo standard errors
%RAFTERY	Raftery diagnostic
%POSTACF	Autocorrelation
%POSTCOR	Correlation matrix
%POSTCOV	Covariance matrix
%POSTINT	Equal-tail and HPD intervals
%POSTSUM	Summary statistics
%SUMINT	Mean, standard deviation, and HPD interval
^*The %GEWEKE and %HEIDEL macros use a different optimization routine than that used in PROC MCMC. As a result, there might be numerical differences in some cases, especially when the sample size is small.

Table 73.47 lists options that are shared by all postprocessing autocall macros. See Table 73.48 for macro-specific options.

Table 73.47: Shared Options

Option	Description
DATA=SAS-data-set	Input data set that contains posterior samples
VAR=variable-list	Specifies the variables on which you want to carry out the calculation.
PRINT=YES \| NO	Displays the results. The default is YES.
OUT=SAS-data-set	Specifies a name for the output SAS data set to contain the results.

Suppose that the data set that contains posterior samples is called post and that the variables of interest are defined in the macro variable &PARMS. The following statements call the %ESS macro and calculates the effective sample sizes for each variable:

%let parms = alpha beta u_1-u_17;
%ESS(data=post, var=&parms);

By default, the ESS estimates are displayed. You can choose not to display the result and save the output to a data set with the following statement:

%ESS(data=post, var=&parms, print=NO, out=eout);

Some of the macros can take additional options, which are listed in Table 73.48.

Table 73.48: Macro-Specific Options

Macro	Option	Description
%ESS	AUTOCORLAG=numeric	Specifies the maximum number of autocorrelation lags used in computing the ESS estimates. By default, AUTOCORLAG=MIN(500, NOBS/4), where NOBS is the sample size of the input data set.
	HIST=YES\|NO	Displays a histogram of all ESS estimates. The default is NO.
%HEIDEL	SALPHA=numeric	Specifies the $\alpha$ level for the stationarity test. By default, SALPHA=0.05.
	HALPHA=numeric	Specifies the $\alpha$ level for the halfwidth test. By default, HALPHA=0.05.
	EPS=numeric	Specifies a small positive number $\epsilon$ such that if the halfwidth is less than $\epsilon$ times the sample mean of the remaining iterations, the halfwidth test is passed. By default, EPS=0.1.
%GEWEKE	FRAC1=numeric	Specifies the earlier portion of the Markov chain used in the test. By default, FRAC1=0.1.
	FRAC2=numeric	Specifies the latter portion of the Markov chain used in the test. By default, FRAC2=0.5.
%MCSE	AUTOCORLAG=numeric	Specifies the maximum number of autocorrelation lags used in computing the Monte Carlo standard error estimates. By default, AUTOCORLAG=MIN(500, NOBS/4), where NOBS is the sample size of the input data set.
%RAFTERY	Q=numeric	Specifies the order of the quantile of interest. By default, Q=0.025.
	R=numeric	Specifies the margin of error for measuring the accuracy of estimation of the quantile. By default, R=0.005.
	S=numeric	Specifies the probability of attaining the accuracy of the estimation of the quantile. By default, S=0.95.
	EPS=numeric	Specifies the tolerance level for the stationary test. By default, EPS=0.001.
%POSTACF	LAGS=%str(numeric-list)	Specifies autocorrelation lags calculated. The default values are 1, 5, 10, and 50.
%POSTINT	ALPHA=value	Specifies the $\alpha$ level $(0<\alpha <1)$ for the interval estimates. By default, ALPHA=0.05.

For example, the following statement calculates and displays autocorrelation at lags 1, 6, 11, 50, and 100. Note that the lags in the numeric-list need to be separated by commas “,”.

%PostACF(data=post, var=&parms, lags=%str(1 to 15 by 5, 50, 100));