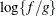The MIXED Procedure

PRIOR Statement

  • PRIOR <distribution> </ options>;

The PRIOR statement enables you to carry out a sampling-based Bayesian analysis in PROC MIXED. It currently operates only with variance component models. Other TYPE= structures are not supported. The analysis produces a SAS data set containing a pseudo-random sample from the joint posterior density of the variance components and other parameters in the mixed model.

The posterior analysis is performed after all other PROC MIXED computations. It begins with the "Posterior Sampling Information" table, which provides basic information about the posterior sampling analysis, including the prior densities, sampling algorithm, sample size, and random number seed. The ODS name of this table is Posterior.

By default, PROC MIXED uses an independence chain algorithm in order to generate the posterior sample (Tierney 1994). This algorithm works by generating a pseudo-random proposal from a convenient base distribution, chosen to be as close as possible to the posterior. The proposal is then retained in the sample with probability proportional to the ratio of weights constructed by taking the ratio of the true posterior to the base density. If a proposal is not accepted, then a duplicate of the previous observation is added to the chain.

In selecting the base distribution, PROC MIXED makes use of the fact that the fixed-effects parameters can be analytically integrated out of the joint posterior, leaving the marginal posterior density of the variance components. In order to better approximate the marginal posterior density of the variance components, PROC MIXED transforms them by using the MIVQUE(0) equations. You can display the selected transformation with the PTRANS option or specify your own with the TDATA= option. The density of the transformed parameters is then approximated by a product of inverted gamma densities (see Gelfand et al. 1990).

To determine the parameters for the inverted gamma densities, PROC MIXED evaluates the logarithm of the posterior density over a grid of points in each of the transformed parameters, and you can display the results of this search with the PSEARCH option. PROC MIXED then performs a linear regression of these values on the logarithm of the inverted gamma density. The resulting base densities are displayed in the "Base Densities" table; the ODS name of this table is Base. You can input different base densities with the BDATA= option.

At the end of the sampling, the "Acceptance Rates" table displays the acceptance rate computed as the number of accepted samples divided by the total number of samples generated. The ODS name of the "Acceptance Rates" table is AccRates.

The OUT= option specifies the output data set containing the posterior sample. PROC MIXED automatically includes all variance component parameters in this data set (labeled COVP1–COVPn), the Type 3 F statistics constructed as in Ghosh (1992) discussing Schervish (1992) (labeled T3Fn), the log values of the posterior (labeled LOGF), the log of the base sampling density (labeled LOGG), and the log of their ratio (labeled LOGRATIO). If you specify the SOLUTION option in the MODEL statement, the data set also contains a random sample from the posterior density of the fixed-effects parameters (labeled BETAn); and if you specify the SOLUTION option in the RANDOM statement, the table contains a random sample from the posterior density of the random-effects parameters (labeled GAMn). PROC MIXED also generates additional variables corresponding to any CONTRAST , ESTIMATE , or LSMEANS statement that you specify.

Subsequently, you can use SAS/INSIGHT or the UNIVARIATE, CAPABILITY, or KDE procedure to analyze the posterior sample.

The prior density of the variance components is, by default, a noninformative version of Jeffreys’ prior (Box and Tiao 1973). You can also specify informative priors with the DATA= option or a flat (equal to 1) prior for the variance components. 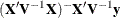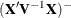The prior density of the fixed-effects parameters is assumed to be flat (equal to 1), and the resulting posterior is conditionally multivariate normal (conditioning on the variance component parameters) with mean $(\mb{X}’\mb{V}^{-1}\mb{X})^-\mb{X}’\mb{V}^{-1}\mb{y}$ and variance $(\mb{X}’\mb{V}^{-1}\mb{X})^-$.

Table 77.14 summarizes the options available in the PRIOR statement.

Table 77.14: PRIOR Statement Options

Option

Description

DATA=

Inputs the prior densities of the variance components

JEFFREYS

Specifies a noninformative reference version of Jeffreys’ prior

FLAT

Specifies a prior density equal to 1 everywhere

ALG=

Specifies the algorithm used for generating the posterior sample

BDATA=

Inputs the base densities used by the sampling algorithm

GRID=

Specifies a grid of values over which to evaluate the posterior density

GRIDT=

Specifies a transformed grid of values over which to evaluate the posterior density

IFACTOR=

An alias for the SFACTOR= option

LOGNOTE=

Writes a note to the log after generating the sample

LOGRBOUND=

Specifies the bounding constant for rejection sampling

NSAMPLE=

Specifies the number of posterior samples to generate

NSEARCH=

Specifies the number of posterior evaluations

OUT=

Creates an output data set containing the sample from the posterior density

OUTG=

Creates an output data set from the grid evaluations

OUTGT=

Creates an output data set from the transformed grid evaluations

PSEARCH

Displays the search used to determine the parameters for the inverted gamma densities

PTRANS

Displays the transformation of the variance components

SEED=

Specifies an integer used to start the pseudo-random number generator

SFACTOR=

Adjusts the search range of the transformed parameters

TDATA=

Inputs the transformation used by the sampling algorithm

TRANS=

Specifies the algorithm that determines the transformation of the covariance parameters

UPDATE=

An alias for the LOGNOTE= option


The distribution argument in the PRIOR statement determines the prior density for the variance component parameters of your mixed model. Valid values are as follows.

DATA=

enables you to input the prior densities of the variance components used by the sampling algorithm. This data set must contain the Type and Parm1–Parmn variables, where n is the largest number of parameters among each of the base densities. The format of the DATA= data set matches that created by PROC MIXED in the "Base Densities" table, so you can output the densities from one run and use them as input for a subsequent run.

JEFFREYS

specifies a noninformative reference version of Jeffreys’ prior constructed by using the square root of the determinant of the expected information matrix as in (1.3.92) of Box and Tiao (1973). This is the default prior.

FLAT

specifies a prior density equal to 1 everywhere, making the likelihood function the posterior.

You can specify the following options in the PRIOR statement after a slash (/).

ALG=IC | INDCHAIN
ALG=IS | IMPSAMP
ALG=RS | REJSAMP
ALG=RWC | RWCHAIN

specifies the algorithm used for generating the posterior sample. The ALG=IC option requests an independence chain algorithm, and it is the default. The option ALG=IS requests importance sampling, ALG=RS requests rejection sampling, and ALG=RWC requests a random walk chain. For more information about these techniques, see Ripley (1987); Smith and Gelfand (1992); Tierney (1994).

BDATA=

enables you to input the base densities used by the sampling algorithm. This data set must contain the Type and Parm1–Parmn variables, where n is the largest number of parameters among each of the base densities. The format of the BDATA= data set matches that created by PROC MIXED in the "Base Densities" table, so you can output the densities from one run and use them as input for a subsequent run.

GRID=(value-list)

specifies a grid of values over which to evaluate the posterior density. The value-list syntax is the same as in the PARMS statement, and you must specify an output data set name with the OUTG= option.

GRIDT=(value-list)

specifies a transformed grid of values over which to evaluate the posterior density. The value-list syntax is the same as in the PARMS statement, and you must specify an output data set name with the OUTGT= option.

IFACTOR=number

is an alias for the SFACTOR= option.

LOGNOTE=number

instructs PROC MIXED to write a note to the SAS log after it generates the sample corresponding to each multiple of number. This is useful for monitoring the progress of CPU-intensive runs.

LOGRBOUND=number

specifies the bounding constant for rejection sampling. The value of number equals the maximum of $\log \{ f/g\} $ over the variance component parameter space, where f is the posterior density and g is the product inverted gamma densities used to perform rejection sampling.

When performing the rejection sampling, you might encounter the following message: 

   WARNING: The log ratio bound of LL was violated at sample XX.

When this occurs, PROC MIXED reruns an optimization algorithm to determine a new log upper bound and then restarts the rejection sampling. The resulting OUT= data set contains all observations that have been generated; therefore, assuming that you have requested N samples, you should retain only the final N observations in this data set for analysis purposes.

NSAMPLE=number

specifies the number of posterior samples to generate. The default is 1000, but more accurate results are obtained with larger samples such as 10000.

NSEARCH=number

specifies the number of posterior evaluations PROC MIXED makes for each transformed parameter in determining the parameters for the inverted gamma densities. The default is 20.

OUT=SAS-data-set

creates an output data set containing the sample from the posterior density.

OUTG=SAS-data-set

creates an output data set from the grid evaluations specified in the GRID= option.

OUTGT=SAS-data-set

creates an output data set from the transformed grid evaluations specified in the GRIDT= option.

PSEARCH

displays the search used to determine the parameters for the inverted gamma densities. The ODS name of the table is Search.

PTRANS

displays the transformation of the variance components. The ODS name of the table is Trans.

SEED=number

specifies an integer used to start the pseudo-random number generator for the simulation. If you do not specify a seed, or if you specify a value less than or equal to zero, the seed is by default generated from reading the time of day from the computer clock. You should use a positive seed (less than $2^{31}-1$) whenever you want to duplicate the sample in another run of PROC MIXED.

SFACTOR=number

enables you to adjust the range over which PROC MIXED searches the transformed parameters in order to determine the parameters for the inverted gamma densities. PROC MIXED determines the range by first transforming the estimates from the standard PROC MIXED analysis (REML, ML, or MIVQUE0, depending upon which estimation method you select). It then multiplies and divides the transformed estimates by $2*$number to obtain upper and lower bounds, respectively. Transformed values that produce negative variance components in the original scale are not included in the search. The default value is 1; number must be greater than 0.5.

TDATA=SAS-data-set

enables you to input the transformation of the covariance parameters used by the sampling algorithm. This data set should contain the CovP1–CovPn variables. The format of the TDATA= data set matches that created by PROC MIXED in the Trans table, so you can output the transformation from one run and use it as input for a subsequent run.

TRANS=EXPECTED | MIVQUE0 | OBSERVED

specifies the particular algorithm used to determine the transformation of the covariance parameters. The default is MIVQUE0, indicating a transformation based on the MIVQUE(0) equations. The other two options indicate the type of Hessian matrix used in constructing the transformation via a Cholesky root.

UPDATE=number

is an alias for the LOGNOTE= option.