The MIXED Procedure
Example 77.5 Random Coefficients
This example comes from a pharmaceutical stability data simulation performed by Obenchain (1990). The observed responses are replicate assay results, expressed in percent of label claim, at various shelf ages, expressed in months. The desired mixed model involves three batches of product that differ randomly in intercept (initial potency) and slope (degradation rate). This type of model is also known as a hierarchical or multilevel model (Singer 1998; Sullivan, Dukes, and Losina 1999).
The SAS statements are as follows:
data rc;
input Batch Month @@;
Monthc = Month;
do i = 1 to 6;
input Y @@;
output;
end;
datalines;
1 0 101.2 103.3 103.3 102.1 104.4 102.4
1 1 98.8 99.4 99.7 99.5 . .
1 3 98.4 99.0 97.3 99.8 . .
1 6 101.5 100.2 101.7 102.7 . .
1 9 96.3 97.2 97.2 96.3 . .
1 12 97.3 97.9 96.8 97.7 97.7 96.7
2 0 102.6 102.7 102.4 102.1 102.9 102.6
2 1 99.1 99.0 99.9 100.6 . .
2 3 105.7 103.3 103.4 104.0 . .
2 6 101.3 101.5 100.9 101.4 . .
2 9 94.1 96.5 97.2 95.6 . .
2 12 93.1 92.8 95.4 92.2 92.2 93.0
3 0 105.1 103.9 106.1 104.1 103.7 104.6
3 1 102.2 102.0 100.8 99.8 . .
3 3 101.2 101.8 100.8 102.6 . .
3 6 101.1 102.0 100.1 100.2 . .
3 9 100.9 99.5 102.2 100.8 . .
3 12 97.8 98.3 96.9 98.4 96.9 96.5
;
proc mixed data=rc; class Batch; model Y = Month / s; random Int Month / type=un sub=Batch s; run;
In the DATA step, Monthc is created as a duplicate of Month in order to enable both a continuous and a classification version of the same variable. The variable Monthc is used in a subsequent analysis
In the PROC MIXED statements, Batch is listed as the only classification variable. The fixed effect Month in the MODEL
statement is not declared as a classification variable; thus it models a linear trend in time. An intercept is included as
a fixed effect by default, and the S option requests that the fixed-effects parameter estimates be produced.
The two random effects are Int and Month, modeling random intercepts and slopes, respectively. Note that Intercept and Month are used as both fixed and random effects. The TYPE=UN
option in the RANDOM
statement specifies an unstructured covariance matrix for the random intercept and slope effects. In mixed model notation,
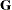 is block diagonal with unstructured 2
is block diagonal with unstructured 2 2 blocks. Each block corresponds to a different level of
2 blocks. Each block corresponds to a different level of Batch, which is the SUBJECT=
effect. The unstructured type provides a mechanism for estimating the correlation between the random coefficients. The S
option requests the production of the random-effects parameter estimates.
The results from this analysis are shown in Output 77.5.1–Output 77.5.9. The "Unstructured" covariance structure in Output 77.5.1 applies to 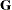 here.
here.
Output 77.5.1: Model Information in Random Coefficients Analysis
Batch is the only classification variable in this analysis, and it has three levels (Output 77.5.2).
Output 77.5.2: Random Coefficients Analysis (continued)
The "Dimensions" table in Output 77.5.3 indicates that there are three subjects (corresponding to batches). The 24 observations not used correspond to the missing
values of Y in the input data set.
Output 77.5.3: Random Coefficients Analysis (continued)
As Output 77.5.4 shows, only one iteration is required for convergence.
Output 77.5.4: Random Coefficients Analysis (continued)
The Estimate column in Output 77.5.5 lists the estimated elements of the unstructured 2 2 matrix comprising the blocks of
2 matrix comprising the blocks of 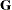 . Note that the random coefficients are negatively correlated.
. Note that the random coefficients are negatively correlated.
Output 77.5.5: Random Coefficients Analysis (continued)
The null model likelihood ratio test indicates a significant improvement over the null model consisting of no random effects and a homogeneous residual error (Output 77.5.6).
Output 77.5.6: Random Coefficients Analysis (continued)
The fixed-effects estimates represent the estimated means for the random intercept and slope, respectively (Output 77.5.7).
Output 77.5.7: Random Coefficients Analysis (continued)
The random-effects estimates represent the estimated deviation from the mean intercept and slope for each batch (Output 77.5.8). Therefore, the intercept for the first batch is close to 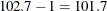 , while the intercepts for the other two batches are greater than 102.7. The second batch has a slope less than the mean slope
of –0.526, while the other two batches have slopes greater than –0.526.
, while the intercepts for the other two batches are greater than 102.7. The second batch has a slope less than the mean slope
of –0.526, while the other two batches have slopes greater than –0.526.
Output 77.5.8: Random Coefficients Analysis (continued)
| Solution for Random Effects | ||||||
|---|---|---|---|---|---|---|
| Effect | Batch | Estimate | Std Err Pred | DF | t Value | Pr > |t| |
| Intercept | 1 | -1.0010 | 0.6842 | 78 | -1.46 | 0.1474 |
| Month | 1 | 0.1287 | 0.1245 | 78 | 1.03 | 0.3047 |
| Intercept | 2 | 0.3934 | 0.6842 | 78 | 0.58 | 0.5669 |
| Month | 2 | -0.2060 | 0.1245 | 78 | -1.65 | 0.1021 |
| Intercept | 3 | 0.6076 | 0.6842 | 78 | 0.89 | 0.3772 |
| Month | 3 | 0.07731 | 0.1245 | 78 | 0.62 | 0.5365 |
The F statistic in the "Type 3 Tests of Fixed Effects" table in Output 77.5.9 is the square of the t statistic used in the test of Month in the preceding "Solution for Fixed Effects" table (compare Output 77.5.7 and Output 77.5.9). Both statistics test the null hypothesis that the slope assigned to Month equals 0, and this hypothesis can barely be rejected at the 5% level.
Output 77.5.9: Random Coefficients Analysis (continued)
It is also possible to fit a random coefficients model with error terms that follow a nested structure (Fuller and Battese 1973). The following SAS statements represent one way of doing this:
proc mixed data=rc; class Batch Monthc; model Y = Month / s; random Int Month Monthc / sub=Batch s; run;
The variable Monthc is added to the CLASS
and RANDOM
statements, and it models the nested errors. Note that Month and Monthc are continuous and classification versions of the same variable. Also, the TYPE=UN
option is dropped from the RANDOM
statement, resulting in the default variance components model instead of correlated random coefficients. The results from
this analysis are shown in Output 77.5.10.
Output 77.5.10: Random Coefficients with Nested Errors Analysis
For this analysis, the Newton-Raphson algorithm requires five iterations and nine likelihood evaluations to achieve convergence. The missing value in the Criterion column in iteration 1 indicates that a boundary constraint has been dropped.
The estimate for the Intercept variance component equals 0. This occurs frequently in practice and indicates that the restricted likelihood is maximized
by setting this variance component equal to 0. Whenever a zero variance component estimate occurs, the following note appears
in the SAS log:
NOTE: Estimated G matrix is not positive definite.
The remaining variance component estimates are positive, and the estimate corresponding to the nested errors (MONTHC) is much larger than the other two.
A comparison of AIC and BIC for this model with those of the previous model favors the nested error model (compare Output 77.5.11 and Output 77.5.6). Strictly speaking, a likelihood ratio test cannot be carried out between the two models because one is not contained in the other; however, a cautious comparison of likelihoods can be informative.
Output 77.5.11: Random Coefficients with Nested Errors Analysis (continued)
The better-fitting covariance model affects the standard errors of the fixed-effects parameter estimates more than the estimates themselves (Output 77.5.12).
Output 77.5.12: Random Coefficients with Nested Errors Analysis (continued)
The random-effects solution provides the empirical best linear unbiased predictions (EBLUPs) for the realizations of the random intercept, slope, and nested errors (Output 77.5.13). You can use these values to compare batches and months.
Output 77.5.13: Random Coefficients with Nested Errors Analysis (continued)
| Solution for Random Effects | |||||||
|---|---|---|---|---|---|---|---|
| Effect | Batch | Monthc | Estimate | Std Err Pred | DF | t Value | Pr > |t| |
| Intercept | 1 | 0 | . | . | . | . | |
| Month | 1 | -0.00028 | 0.09268 | 66 | -0.00 | 0.9976 | |
| Monthc | 1 | 0 | 0.2191 | 0.7896 | 66 | 0.28 | 0.7823 |
| Monthc | 1 | 1 | -2.5690 | 0.7571 | 66 | -3.39 | 0.0012 |
| Monthc | 1 | 3 | -2.3067 | 0.6865 | 66 | -3.36 | 0.0013 |
| Monthc | 1 | 6 | 1.8726 | 0.7328 | 66 | 2.56 | 0.0129 |
| Monthc | 1 | 9 | -1.2350 | 0.9300 | 66 | -1.33 | 0.1888 |
| Monthc | 1 | 12 | 0.7736 | 1.1992 | 66 | 0.65 | 0.5211 |
| Intercept | 2 | 0 | . | . | . | . | |
| Month | 2 | -0.07571 | 0.09268 | 66 | -0.82 | 0.4169 | |
| Monthc | 2 | 0 | -0.00621 | 0.7896 | 66 | -0.01 | 0.9938 |
| Monthc | 2 | 1 | -2.2126 | 0.7571 | 66 | -2.92 | 0.0048 |
| Monthc | 2 | 3 | 3.1063 | 0.6865 | 66 | 4.53 | <.0001 |
| Monthc | 2 | 6 | 2.0649 | 0.7328 | 66 | 2.82 | 0.0064 |
| Monthc | 2 | 9 | -1.4450 | 0.9300 | 66 | -1.55 | 0.1250 |
| Monthc | 2 | 12 | -2.4405 | 1.1992 | 66 | -2.04 | 0.0459 |
| Intercept | 3 | 0 | . | . | . | . | |
| Month | 3 | 0.07600 | 0.09268 | 66 | 0.82 | 0.4152 | |
| Monthc | 3 | 0 | 1.9574 | 0.7896 | 66 | 2.48 | 0.0157 |
| Monthc | 3 | 1 | -0.8850 | 0.7571 | 66 | -1.17 | 0.2466 |
| Monthc | 3 | 3 | 0.3006 | 0.6865 | 66 | 0.44 | 0.6629 |
| Monthc | 3 | 6 | 0.7972 | 0.7328 | 66 | 1.09 | 0.2806 |
| Monthc | 3 | 9 | 2.0059 | 0.9300 | 66 | 2.16 | 0.0347 |
| Monthc | 3 | 12 | 0.002293 | 1.1992 | 66 | 0.00 | 0.9985 |
Output 77.5.14: Random Coefficients with Nested Errors Analysis (continued)
The test of Month is similar to that from the previous model, although it is no longer significant at the 5% level (Output 77.5.14).
