The MIXED Procedure

PROC MIXED is a generalization of the GLM procedure in the sense that PROC GLM fits standard linear models, and PROC MIXED fits the wider class of mixed linear models. Both procedures have similar CLASS , MODEL , CONTRAST , ESTIMATE , and LSMEANS statements, but their RANDOM and REPEATED statements differ (see the following paragraphs). Both procedures use the non-full-rank model parameterization, although the sorting of classification levels can differ between the two. PROC MIXED computes only Type I–Type III tests of fixed effects, while PROC GLM computes Types I–IV.

The RANDOM statement in PROC MIXED incorporates random effects constituting the 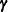vector in the mixed model. However, in PROC GLM, effects specified in the RANDOM statement are still treated as fixed as far as the model fit is concerned, and they serve only to produce corresponding expected mean squares. These expected mean squares lead to the traditional ANOVA estimates of variance components. PROC MIXED computes REML and ML estimates of variance parameters, which are generally preferred to the ANOVA estimates (Searle 1988; Harville 1988; Searle, Casella, and McCulloch 1992). Optionally, PROC MIXED also computes MIVQUE0 estimates, which are similar to ANOVA estimates.

The REPEATED statement in PROC MIXED is used to specify covariance structures for repeated measurements on subjects, while the REPEATED statement in PROC GLM is used to specify various transformations with which to conduct the traditional univariate or multivariate tests. In repeated measures situations, the mixed model approach used in PROC MIXED is more flexible and more widely applicable than either the univariate or multivariate approach. In particular, the mixed model approach provides a larger class of covariance structures and a better mechanism for handling missing values (Wolfinger and Chang 1995).

PROC MIXED subsumes the VARCOMP procedure. PROC MIXED provides a wide variety of covariance structures, while PROC VARCOMP estimates only simple random effects. PROC MIXED carries out several analyses that are absent in PROC VARCOMP, including the estimation and testing of linear combinations of fixed and random effects.

The ARIMA and AUTOREG procedures provide more time series structures than PROC MIXED, although they do not fit variance component models. The CALIS procedure fits general covariance matrices, but the fixed effects structure of the model is formed differently than in PROC MIXED. The LATTICE and NESTED procedures fit special types of mixed linear models that can also be handled in PROC MIXED, although PROC MIXED might run slower because of its more general algorithm. The TSCSREG procedure analyzes time series cross-sectional data, and it fits some structures not available in PROC MIXED.

The GLIMMIX procedure fits generalized linear mixed models (GLMMs). Linear mixed models—where the data are normally distributed, given the random effects—are in the class of GLMMs. The MIXED procedure can estimate covariance parameters with ANOVA methods that are not available in the GLIMMIX procedure (see METHOD= TYPE1, METHOD= TYPE2, and METHOD= TYPE3 in the PROC MIXED statement). Also, PROC MIXED can perform a sampling-based Bayesian analysis through the PRIOR statement, and the procedure supports certain Kronecker-type covariance structures. These features are not available in the GLIMMIX procedure. The GLIMMIX procedure, on the other hand, accommodates nonnormal data and offers a broader array of post-processing features than the MIXED procedure.