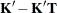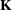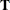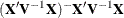The MIXED Procedure
CONTRAST Statement
-
CONTRAST ’label’ <fixed-effect values …> <random-effect values …>, …</ options>;
The CONTRAST statement provides a mechanism for obtaining custom hypothesis tests. It is patterned after the CONTRAST statement in PROC GLM, although it has been extended to include random effects. This enables you to select an appropriate inference space (McLean, Sanders, and Stroup 1991).
You can test the hypothesis 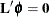 ,
where
,
where 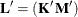 and
and 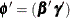 , in several inference spaces. The inference space corresponds to the choice of
, in several inference spaces. The inference space corresponds to the choice of 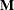 . When
. When 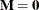 , your inferences apply to the entire population from which the random effects are sampled; this is known as the broad inference space. When all elements of
, your inferences apply to the entire population from which the random effects are sampled; this is known as the broad inference space. When all elements of 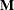 are nonzero, your inferences apply only to the observed levels of the random effects. This is known as the narrow inference space, and you can also choose it by specifying all of the random effects as fixed. The GLM procedure uses the
narrow inference space. Finally, by setting to zero the portions of
are nonzero, your inferences apply only to the observed levels of the random effects. This is known as the narrow inference space, and you can also choose it by specifying all of the random effects as fixed. The GLM procedure uses the
narrow inference space. Finally, by setting to zero the portions of 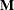 corresponding to selected main effects and interactions, you can choose intermediate inference spaces. The broad inference space is usually the most appropriate, and it is used when you do not specify any random
effects in the CONTRAST statement.
corresponding to selected main effects and interactions, you can choose intermediate inference spaces. The broad inference space is usually the most appropriate, and it is used when you do not specify any random
effects in the CONTRAST statement.
The CONTRAST statement has the following arguments:
- label
-
identifies the contrast in the table. A label is required for every contrast specified. Labels can be up to 200 characters and must be enclosed in quotes.
- fixed-effect
-
identifies an effect that appears in the MODEL statement. The keyword INTERCEPT can be used as an effect when an intercept is fitted in the model. You do not need to include all effects that are in the MODEL statement.
- random-effect
-
identifies an effect that appears in the RANDOM statement. The first random effect must follow a vertical bar (|); however, random effects do not have to be specified.
- values
-
are constants that are elements of the
 matrix associated with the fixed and random effects.
matrix associated with the fixed and random effects.
The rows of 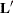 are specified in order and are separated by commas. The rows of the
are specified in order and are separated by commas. The rows of the 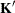 component of
component of 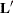 are specified on the left side of the vertical bars (|). These rows test the fixed effects and are, therefore, checked for
estimability. The rows of the
are specified on the left side of the vertical bars (|). These rows test the fixed effects and are, therefore, checked for
estimability. The rows of the 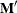 component of
component of 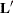 are specified on the right side of the vertical bars. They test the random effects, and no estimability checking is necessary.
are specified on the right side of the vertical bars. They test the random effects, and no estimability checking is necessary.
If PROC MIXED finds the fixed-effects portion of the specified contrast to be nonestimable (see the SINGULAR= option), then it displays a message in the log.
The following CONTRAST statement reproduces the F test for the effect A in the split-plot example (see Example 77.1):
contrast 'A broad'
A 1 -1 0 A*B .5 .5 -.5 -.5 0 0 ,
A 1 0 -1 A*B .5 .5 0 0 -.5 -.5 / df=6;
Note that no random effects are specified in the preceding contrast; thus, the inference space is broad. The resulting F test has two numerator degrees of freedom because 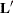 has two rows. The denominator degrees of freedom is, by default, the residual degrees of freedom (9), but the DF=
option changes the denominator degrees of freedom to 6.
has two rows. The denominator degrees of freedom is, by default, the residual degrees of freedom (9), but the DF=
option changes the denominator degrees of freedom to 6.
The following CONTRAST statement reproduces the F test for A when Block and A*Block are considered fixed effects (the narrow inference space):
contrast 'A narrow'
A 1 -1 0
A*B .5 .5 -.5 -.5 0 0 |
A*Block .25 .25 .25 .25
-.25 -.25 -.25 -.25
0 0 0 0 ,
A 1 0 -1
A*B .5 .5 0 0 -.5 -.5 |
A*Block .25 .25 .25 .25
0 0 0 0
-.25 -.25 -.25 -.25 ;
The preceding contrast does not contain coefficients for B and Block, because they cancel out in estimated differences between levels of A. Coefficients for B and Block are necessary to estimate the mean of one of the levels of A in the narrow inference space (see Example 77.1).
If the elements of  are not specified for an effect that contains a specified effect, then the elements of the specified effect are automatically
"filled in" over the levels of the higher-order effect. This feature is designed to preserve estimability for cases where
there are complex higher-order effects. The coefficients for the higher-order effect are determined by equitably distributing
the coefficients of the lower-level effect, as in the construction of least squares means. In addition, if the intercept is
specified, it is distributed over all classification effects that are not contained by any other specified effect. If an effect
is not specified and does not contain any specified effects, then all of its coefficients in
are not specified for an effect that contains a specified effect, then the elements of the specified effect are automatically
"filled in" over the levels of the higher-order effect. This feature is designed to preserve estimability for cases where
there are complex higher-order effects. The coefficients for the higher-order effect are determined by equitably distributing
the coefficients of the lower-level effect, as in the construction of least squares means. In addition, if the intercept is
specified, it is distributed over all classification effects that are not contained by any other specified effect. If an effect
is not specified and does not contain any specified effects, then all of its coefficients in  are set to 0. You can override this behavior by specifying coefficients for the higher-order effect.
are set to 0. You can override this behavior by specifying coefficients for the higher-order effect.
If too many values are specified for an effect, the extra ones are ignored; if too few are specified, the remaining ones are
set to 0. If no random effects are specified, the vertical bar can be omitted; otherwise, it must be present. If a SUBJECT=
effect is used in the RANDOM
statement, then the coefficients specified for the effects in the RANDOM
statement are equitably distributed across the levels of the SUBJECT effect. You can use the E
option to see exactly which  matrix is used.
matrix is used.
The SUBJECT and GROUP options in the CONTRAST statement are useful for the case when a SUBJECT= or GROUP= variable appears in the RANDOM statement, and you want to contrast different subjects or groups. By default, CONTRAST statement coefficients on random effects are distributed equally across subjects and groups.
PROC MIXED handles missing level combinations of classification variables similarly to the way PROC GLM does. Both procedures delete fixed-effects parameters corresponding to missing levels in order to preserve estimability. However, PROC MIXED does not delete missing level combinations for random-effects parameters because linear combinations of the random-effects parameters are always estimable. These conventions can affect the way you specify your CONTRAST coefficients.
The CONTRAST statement computes the statistic
![\[ F = \frac{ \left[\begin{array}{c} \widehat{\bbeta } \\ \widehat{\bgamma } \end{array} \right]'\mb{L}(\mb{L}'\widehat{\mb{C}}\mb{L})^{-1} \mb{L}' \left[\begin{array}{c} \widehat{\bbeta } \\ \widehat{\bgamma } \end{array} \right]}{r} \]](images/statug_mixed0073.png)
where 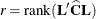 , and approximates its distribution with an F distribution. In this expression,
, and approximates its distribution with an F distribution. In this expression, 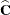 is an estimate of the generalized inverse of the coefficient matrix in the mixed model equations.
For more information about this F statistic, see the section Inference and Test Statistics.
is an estimate of the generalized inverse of the coefficient matrix in the mixed model equations.
For more information about this F statistic, see the section Inference and Test Statistics.
The numerator degrees of freedom in the F approximation are
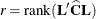 , and the denominator degrees of freedom are taken from the "Tests of Fixed Effects" table and corresponds to the final effect
you list in the CONTRAST statement. You can change the denominator degrees of freedom by using the DF=
option.
, and the denominator degrees of freedom are taken from the "Tests of Fixed Effects" table and corresponds to the final effect
you list in the CONTRAST statement. You can change the denominator degrees of freedom by using the DF=
option.
You can specify the following options in the CONTRAST statement after a slash (/).