The MIXED Procedure
Example 77.6 Line-Source Sprinkler Irrigation
These data appear in Hanks et al. (1980); Johnson, Chaudhuri, and Kanemasu (1983); Stroup (1989b). Three cultivars (Cult) of winter wheat are randomly assigned to rectangular plots within each of three blocks (Block). The nine plots are located side by side, and a line-source sprinkler is placed through the middle. Each plot is subdivided
into twelve subplots—six to the north of the line source, six to the south (Dir). The two plots closest to the line source represent the maximum irrigation level (Irrig=6), the two next-closest plots represent the next-highest level (Irrig=5), and so forth.
This example is a case where both 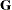 and
and 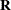 can be modeled. One of Stroup’s models specifies a diagonal
can be modeled. One of Stroup’s models specifies a diagonal 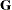 containing the variance components for
containing the variance components for Block, Block*Dir, and Block*Irrig, and a Toeplitz 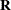 with four bands. The SAS statements to fit this model and carry out some further analyses follow.
with four bands. The SAS statements to fit this model and carry out some further analyses follow.
Caution: This analysis can require considerable CPU time.
data line;
length Cult$ 8;
input Block Cult$ @;
row = _n_;
do Sbplt=1 to 12;
if Sbplt le 6 then do;
Irrig = Sbplt;
Dir = 'North';
end; else do;
Irrig = 13 - Sbplt;
Dir = 'South';
end;
input Y @; output;
end;
datalines;
1 Luke 2.4 2.7 5.6 7.5 7.9 7.1 6.1 7.3 7.4 6.7 3.8 1.8
1 Nugaines 2.2 2.2 4.3 6.3 7.9 7.1 6.2 5.3 5.3 5.2 5.4 2.9
1 Bridger 2.9 3.2 5.1 6.9 6.1 7.5 5.6 6.5 6.6 5.3 4.1 3.1
2 Nugaines 2.4 2.2 4.0 5.8 6.1 6.2 7.0 6.4 6.7 6.4 3.7 2.2
2 Bridger 2.6 3.1 5.7 6.4 7.7 6.8 6.3 6.2 6.6 6.5 4.2 2.7
2 Luke 2.2 2.7 4.3 6.9 6.8 8.0 6.5 7.3 5.9 6.6 3.0 2.0
3 Nugaines 1.8 1.9 3.7 4.9 5.4 5.1 5.7 5.0 5.6 5.1 4.2 2.2
3 Luke 2.1 2.3 3.7 5.8 6.3 6.3 6.5 5.7 5.8 4.5 2.7 2.3
3 Bridger 2.7 2.8 4.0 5.0 5.2 5.2 5.9 6.1 6.0 4.3 3.1 3.1
;
proc mixed;
class Block Cult Dir Irrig;
model Y = Cult|Dir|Irrig@2;
random Block Block*Dir Block*Irrig;
repeated / type=toep(4) sub=Block*Cult r;
lsmeans Cult|Irrig;
estimate 'Bridger vs Luke' Cult 1 -1 0;
estimate 'Linear Irrig' Irrig -5 -3 -1 1 3 5;
estimate 'B vs L x Linear Irrig' Cult*Irrig
-5 -3 -1 1 3 5 5 3 1 -1 -3 -5;
run;
The preceding statements use the bar operator ( | ) and the at sign (@) to specify all two-factor interactions between Cult, Dir, and Irrig as fixed effects.
The RANDOM
statement sets up the 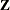 and
and 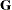 matrices corresponding to the random effects
matrices corresponding to the random effects Block, Block*Dir, and Block*Irrig.
In the REPEATED
statement, the TYPE=TOEP
(4) option sets up the blocks of the 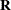 matrix to be Toeplitz with four bands below and including the main diagonal. The subject effect is
matrix to be Toeplitz with four bands below and including the main diagonal. The subject effect is Block*Cult, and it produces nine 12 12 blocks. The R
option requests that the first block of
12 blocks. The R
option requests that the first block of 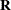 be displayed.
be displayed.
Least squares means (LSMEANS
) are requested for Cult, Irrig, and Cult*Irrig, and a few ESTIMATE
statements are specified to illustrate some linear combinations of the fixed effects.
The results from this analysis are shown in Output 77.6.1.
The "Covariance Structures" row in Output 77.6.1 reveals the two different structures assumed for 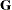 and
and 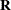 .
.
Output 77.6.1: Model Information in Line-Source Sprinkler Analysis
The levels of each classification variable are listed as a single string in the Values column, regardless of whether the levels are numeric or character (Output 77.6.2).
Output 77.6.2: Class Level Information
Even though there is a SUBJECT= effect in the REPEATED statement, the analysis considers all of the data to be from one subject because there is no corresponding SUBJECT= effect in the RANDOM statement (Output 77.6.3).
Output 77.6.3: Model Dimensions and Number of Observations
The Newton-Raphson algorithm converges successfully in seven iterations (Output 77.6.4).
Output 77.6.4: Iteration History and Convergence Status
The first block of the estimated 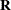 matrix has the TOEP(4) structure, and the observations that are three plots apart exhibit a negative correlation (Output 77.6.5).
matrix has the TOEP(4) structure, and the observations that are three plots apart exhibit a negative correlation (Output 77.6.5).
Output 77.6.5: Estimated R Matrix for the First Subject
| Estimated R Matrix for Block*Cult 1 Bridger | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Row | Col1 | Col2 | Col3 | Col4 | Col5 | Col6 | Col7 | Col8 | Col9 | Col10 | Col11 | Col12 |
| 1 | 0.2850 | 0.007986 | 0.001452 | -0.09253 | ||||||||
| 2 | 0.007986 | 0.2850 | 0.007986 | 0.001452 | -0.09253 | |||||||
| 3 | 0.001452 | 0.007986 | 0.2850 | 0.007986 | 0.001452 | -0.09253 | ||||||
| 4 | -0.09253 | 0.001452 | 0.007986 | 0.2850 | 0.007986 | 0.001452 | -0.09253 | |||||
| 5 | -0.09253 | 0.001452 | 0.007986 | 0.2850 | 0.007986 | 0.001452 | -0.09253 | |||||
| 6 | -0.09253 | 0.001452 | 0.007986 | 0.2850 | 0.007986 | 0.001452 | -0.09253 | |||||
| 7 | -0.09253 | 0.001452 | 0.007986 | 0.2850 | 0.007986 | 0.001452 | -0.09253 | |||||
| 8 | -0.09253 | 0.001452 | 0.007986 | 0.2850 | 0.007986 | 0.001452 | -0.09253 | |||||
| 9 | -0.09253 | 0.001452 | 0.007986 | 0.2850 | 0.007986 | 0.001452 | -0.09253 | |||||
| 10 | -0.09253 | 0.001452 | 0.007986 | 0.2850 | 0.007986 | 0.001452 | ||||||
| 11 | -0.09253 | 0.001452 | 0.007986 | 0.2850 | 0.007986 | |||||||
| 12 | -0.09253 | 0.001452 | 0.007986 | 0.2850 | ||||||||
Output 77.6.6 lists the estimated covariance parameters from both 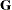 and
and 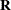 . The first three are the variance components making up the diagonal
. The first three are the variance components making up the diagonal 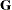 , and the final four make up the Toeplitz structure in the blocks of
, and the final four make up the Toeplitz structure in the blocks of 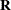 . The Residual row corresponds to the variance of the Toeplitz structure, and it represents the parameter profiled out during
the optimization process.
. The Residual row corresponds to the variance of the Toeplitz structure, and it represents the parameter profiled out during
the optimization process.
Output 77.6.6: Estimated Covariance Parameters
The "–2 Res Log Likelihood" value in Output 77.6.7 is the same as the final value listed in the "Iteration History" table (Output 77.6.4).
Output 77.6.7: Fit Statistics Based on the Residual Log Likelihood
Every fixed effect except for Dir and Cult*Irrig is significant at the 5% level (Output 77.6.8).
Output 77.6.8: Tests for Fixed Effects
The "Estimates" table lists the results from the various linear combinations of fixed effects specified in the ESTIMATE
statements (Output 77.6.9). Bridger is not significantly different from Luke, and Irrig possesses a strong linear component. This strength appears to be influencing the significance of the interaction.
Output 77.6.9: Estimates
The least squares means shown in Output 77.6.10 are useful in comparing the levels of the various fixed effects. For example, it appears that irrigation levels 5 and 6 have virtually the same effect.
Output 77.6.10: Least Squares Means for Cult, Irrig, and Their Interaction
| Least Squares Means | |||||||
|---|---|---|---|---|---|---|---|
| Effect | Cult | Irrig | Estimate | Standard Error |
DF | t Value | Pr > |t| |
| Cult | Bridger | 5.0306 | 0.2874 | 68 | 17.51 | <.0001 | |
| Cult | Luke | 5.0694 | 0.2874 | 68 | 17.64 | <.0001 | |
| Cult | Nugaines | 4.7222 | 0.2874 | 68 | 16.43 | <.0001 | |
| Irrig | 1 | 2.4222 | 0.3220 | 10 | 7.52 | <.0001 | |
| Irrig | 2 | 3.1833 | 0.3220 | 10 | 9.88 | <.0001 | |
| Irrig | 3 | 5.0556 | 0.3220 | 10 | 15.70 | <.0001 | |
| Irrig | 4 | 6.1889 | 0.3220 | 10 | 19.22 | <.0001 | |
| Irrig | 5 | 6.4000 | 0.3140 | 10 | 20.38 | <.0001 | |
| Irrig | 6 | 6.3944 | 0.3227 | 10 | 19.81 | <.0001 | |
| Cult*Irrig | Bridger | 1 | 2.8500 | 0.3679 | 68 | 7.75 | <.0001 |
| Cult*Irrig | Bridger | 2 | 3.4167 | 0.3679 | 68 | 9.29 | <.0001 |
| Cult*Irrig | Bridger | 3 | 5.1500 | 0.3679 | 68 | 14.00 | <.0001 |
| Cult*Irrig | Bridger | 4 | 6.2500 | 0.3679 | 68 | 16.99 | <.0001 |
| Cult*Irrig | Bridger | 5 | 6.3000 | 0.3463 | 68 | 18.19 | <.0001 |
| Cult*Irrig | Bridger | 6 | 6.2167 | 0.3697 | 68 | 16.81 | <.0001 |
| Cult*Irrig | Luke | 1 | 2.1333 | 0.3679 | 68 | 5.80 | <.0001 |
| Cult*Irrig | Luke | 2 | 2.8667 | 0.3679 | 68 | 7.79 | <.0001 |
| Cult*Irrig | Luke | 3 | 5.2333 | 0.3679 | 68 | 14.22 | <.0001 |
| Cult*Irrig | Luke | 4 | 6.5500 | 0.3679 | 68 | 17.80 | <.0001 |
| Cult*Irrig | Luke | 5 | 6.8833 | 0.3463 | 68 | 19.87 | <.0001 |
| Cult*Irrig | Luke | 6 | 6.7500 | 0.3697 | 68 | 18.26 | <.0001 |
| Cult*Irrig | Nugaines | 1 | 2.2833 | 0.3679 | 68 | 6.21 | <.0001 |
| Cult*Irrig | Nugaines | 2 | 3.2667 | 0.3679 | 68 | 8.88 | <.0001 |
| Cult*Irrig | Nugaines | 3 | 4.7833 | 0.3679 | 68 | 13.00 | <.0001 |
| Cult*Irrig | Nugaines | 4 | 5.7667 | 0.3679 | 68 | 15.67 | <.0001 |
| Cult*Irrig | Nugaines | 5 | 6.0167 | 0.3463 | 68 | 17.37 | <.0001 |
| Cult*Irrig | Nugaines | 6 | 6.2167 | 0.3697 | 68 | 16.81 | <.0001 |
An interesting exercise is to fit other variance-covariance models to these data and to compare them to this one by using likelihood ratio tests, Akaike’s information criterion, or Schwarz’s Bayesian information criterion. In particular, some spatial models are worth investigating (Marx and Thompson 1987; Zimmerman and Harville 1991). The following is one example of spatial model statements:
proc mixed; class Block Cult Dir Irrig; model Y = Cult|Dir|Irrig@2; repeated / type=sp(pow)(Row Sbplt) sub=intercept; run;
The TYPE=SP(POW)
(Row Sbplt) option in the REPEATED
statement requests the spatial power structure, with the two defining coordinate variables being Row and Sbplt. The SUBJECT=
INTERCEPT option indicates that the entire data set is to be considered as one subject, thereby modeling 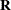 as a dense 108
as a dense 108 108 covariance matrix. See Wolfinger (1993) for further discussion of this example and additional analyses.
108 covariance matrix. See Wolfinger (1993) for further discussion of this example and additional analyses.
