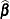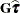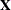-
ABSOLUTE
-
makes the convergence criterion absolute. By default, it is relative
(divided by the current objective function value). See the CONVF
, CONVG
, and CONVH
options in this section for a description of various convergence criteria.
-
ALPHA=number
-
requests that confidence limits be constructed for the covariance
parameter estimates with confidence level 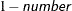 . The value of number must be between 0 and 1; the default is 0.05.
. The value of number must be between 0 and 1; the default is 0.05.
-
ANOVAF
-
The ANOVAF option computes F tests in models with REPEATED
statement and without RANDOM statement by a method similar to that of Brunner, Domhof, and Langer (2002). The method consists of computing special F statistics and adjusting their degrees of freedom. The technique is a generalization of the Greenhouse-Geisser adjustment
in MANOVA models (Greenhouse and Geisser 1959). For more details, see the section F Tests With the ANOVAF Option.
-
ASYCORR
-
produces the asymptotic correlation matrix of the covariance
parameter estimates. It is computed from the corresponding asymptotic covariance matrix (see the description of the ASYCOV
option, which follows). The name of the "Asymptotic Correlation" table is AsyCorr.
-
ASYCOV
-
requests that the asymptotic covariance matrix of the covariance
parameters be displayed. By default, this matrix is the observed inverse Fisher information matrix, which equals 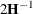 , where
, where 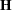 is the Hessian (second derivative) matrix of the objective function. For more information about this matrix, see the section
Covariance Parameter Estimates. When you use the SCORING=
option and PROC MIXED converges without stopping the scoring algorithm, PROC MIXED uses the expected Hessian matrix to compute
the covariance matrix instead of the observed Hessian. The ODS name of the "Asymptotic Covariance" table is AsyCov.
is the Hessian (second derivative) matrix of the objective function. For more information about this matrix, see the section
Covariance Parameter Estimates. When you use the SCORING=
option and PROC MIXED converges without stopping the scoring algorithm, PROC MIXED uses the expected Hessian matrix to compute
the covariance matrix instead of the observed Hessian. The ODS name of the "Asymptotic Covariance" table is AsyCov.
-
CL<=WALD>
-
requests confidence limits for the covariance parameter estimates.
A Satterthwaite approximation is used to construct limits for all parameters that have a lower boundary constraint of zero.
These limits take the form
where 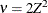 , Z is the Wald statistic
, Z is the Wald statistic 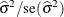 , and the denominators are quantiles of the
, and the denominators are quantiles of the 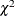 -distribution with
-distribution with  degrees of freedom. See Milliken and Johnson (1992) and Burdick and Graybill (1992) for similar techniques.
degrees of freedom. See Milliken and Johnson (1992) and Burdick and Graybill (1992) for similar techniques.
For all other parameters, Wald Z-scores and normal quantiles are used to construct the limits. Wald limits are also provided for variance components if you
specify the NOBOUND
option. The optional =WALD specification requests Wald limits for all parameters.
The confidence limits are displayed as extra columns in the "Covariance Parameter Estimates" table. The confidence level is
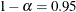 by default; this can be changed with the ALPHA=
option.
by default; this can be changed with the ALPHA=
option.
-
CONVF<=number>
-
requests the relative function convergence criterion with tolerance
number. The relative function convergence criterion is
where 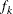 is the value of the objective function at iteration k. To prevent the division by
is the value of the objective function at iteration k. To prevent the division by 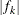 , use the ABSOLUTE
option. The default convergence criterion is CONVH
, and the default tolerance is 1E–8.
, use the ABSOLUTE
option. The default convergence criterion is CONVH
, and the default tolerance is 1E–8.
-
CONVG <=number>
-
requests the relative gradient convergence criterion with tolerance
number. The relative gradient convergence criterion is
where 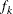 is the value of the objective function, and
is the value of the objective function, and 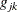 is the jth element of the gradient (first derivative) of the objective function, both at iteration k. To prevent division by
is the jth element of the gradient (first derivative) of the objective function, both at iteration k. To prevent division by 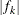 , use the ABSOLUTE
option. The default convergence criterion is CONVH
, and the default tolerance is 1E–8.
, use the ABSOLUTE
option. The default convergence criterion is CONVH
, and the default tolerance is 1E–8.
-
CONVH<=number>
-
requests the relative Hessian convergence criterion with tolerance
number. The relative Hessian convergence criterion is
where 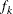 is the value of the objective function,
is the value of the objective function, 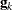 is the gradient (first derivative) of the objective function, and
is the gradient (first derivative) of the objective function, and 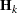 is the Hessian (second derivative) of the objective function, all at iteration k.
is the Hessian (second derivative) of the objective function, all at iteration k.
If 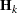 is singular, then PROC MIXED uses the following relative criterion:
is singular, then PROC MIXED uses the following relative criterion:
To prevent the division by 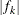 , use the ABSOLUTE
option. The default convergence criterion is CONVH
, and the default tolerance is 1E–8.
, use the ABSOLUTE
option. The default convergence criterion is CONVH
, and the default tolerance is 1E–8.
-
COVTEST
-
produces asymptotic standard errors and Wald Z-tests for the
covariance parameter estimates.
-
DATA=SAS-data-set
-
names the SAS data set to be used by PROC MIXED. The default
is the most recently created data set.
-
DFBW
-
has the same effect as the DDFM=
BW
option in the MODEL
statement.
-
EMPIRICAL
-
computes the estimated variance-covariance matrix of the
fixed-effects parameters by using the asymptotically consistent estimator described in Huber (1967); White (1980); Liang and Zeger (1986); Diggle, Liang, and Zeger (1994). This estimator is commonly referred to as the "sandwich" estimator, and it is computed as follows:
Here, 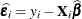 , S is the number of subjects, and matrices with an i subscript are those for the ith subject. You must include the SUBJECT= option in either a RANDOM
or REPEATED
statement for this option to take effect.
, S is the number of subjects, and matrices with an i subscript are those for the ith subject. You must include the SUBJECT= option in either a RANDOM
or REPEATED
statement for this option to take effect.
When you specify the EMPIRICAL option, PROC MIXED adjusts all standard errors and test statistics involving the fixed-effects
parameters. This changes output in the following tables (listed in Table 77.26): Contrast, CorrB, CovB, Diffs, Estimates, InvCovB, LSMeans, Slices, SolutionF, Tests1–Tests3. The OUTP= and OUTPM= data
sets are also affected. Finally, the Satterthwaite and Kenward-Roger degrees of freedom methods are not available if you specify
the EMPIRICAL option.
-
IC
-
displays a table of various information criteria. The criteria
are all in smaller-is-better form, and are described in Table 77.3.
Table 77.3: Information Criteria
|
Criterion
|
Formula
|
Reference
|
|
AIC
|
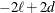
|
Akaike (1974)
|
|
AICC
|
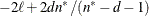
|
Hurvich and Tsai (1989)
|
| |
|
Burnham and Anderson (1998)
|
|
HQIC
|
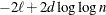 for for 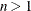
|
Hannan and Quinn (1979)
|
|
BIC
|
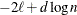 for for 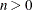
|
Schwarz (1978)
|
|
CAIC
|
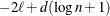 for for 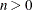
|
Bozdogan (1987)
|
Here 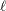 denotes the maximum value of the (possibly restricted) log likelihood, d the dimension of the model, and n the number of observations. In SAS 6 of SAS/STAT software, n equals the number of valid observations for maximum likelihood estimation and
denotes the maximum value of the (possibly restricted) log likelihood, d the dimension of the model, and n the number of observations. In SAS 6 of SAS/STAT software, n equals the number of valid observations for maximum likelihood estimation and 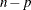 for restricted maximum likelihood estimation, where p equals the rank of
for restricted maximum likelihood estimation, where p equals the rank of 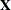 . In later versions, n equals the number of effective subjects as displayed in the "Dimensions" table, unless this value equals 1, in which case
n equals the number of levels of the first random effect you specify in a RANDOM
statement. If the number of effective subjects equals 1 and you have no RANDOM
statements, then n reverts to the SAS 6 values. For AICC (a finite-sample corrected version of AIC),
. In later versions, n equals the number of effective subjects as displayed in the "Dimensions" table, unless this value equals 1, in which case
n equals the number of levels of the first random effect you specify in a RANDOM
statement. If the number of effective subjects equals 1 and you have no RANDOM
statements, then n reverts to the SAS 6 values. For AICC (a finite-sample corrected version of AIC), 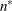 equals the SAS 6 values of n, unless this number is less than d + 2, in which case it equals d + 2. When
equals the SAS 6 values of n, unless this number is less than d + 2, in which case it equals d + 2. When 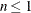 , the value of the HQIC criterion is
, the value of the HQIC criterion is 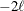 . When n=0, the values of the BIC and CAIC criteria are
. When n=0, the values of the BIC and CAIC criteria are 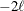 and
and 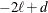 , respectively.
, respectively.
For restricted likelihood estimation, d equals q, the effective number of estimated covariance parameters. In SAS 6, when a parameter estimate lies on a boundary constraint,
then it is still included in the calculation of d, but in later versions it is not. The most common example of this behavior is when a variance component is estimated to equal
zero. For maximum likelihood estimation, d equals 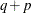 where p is by default the sum of the Type 3 degrees of freedom associated with each fixed effect or the rank of X if you specify
NOTEST
option. The value of d is displayed in the "Information Criteria" table as the value of Parms variable; see Table 77.27.
where p is by default the sum of the Type 3 degrees of freedom associated with each fixed effect or the rank of X if you specify
NOTEST
option. The value of d is displayed in the "Information Criteria" table as the value of Parms variable; see Table 77.27.
The ODS name of the "Information Criteria" table is InfoCrit.
-
INFO
-
is a default option. The creation of the
"Model Information," "Dimensions," and "Number of Observations" tables can be suppressed by using the NOINFO
option.
Note that in SAS 6 this option displays the "Model Information" and "Dimensions" tables.
-
ITDETAILS
-
displays the parameter values at each iteration and enables the
writing of notes to the SAS log pertaining to "infinite likelihood" and "singularities" during Newton-Raphson iterations.
-
LOGNOTE
-
writes periodic notes to the log describing the current status of
computations. It is designed for use with analyses requiring extensive CPU resources.
-
MAXFUNC=number
-
specifies the maximum number of likelihood evaluations in the
optimization process. The default is 150.
-
MAXITER=number
-
specifies the maximum number of iterations. The default is 50.
-
METHOD=REML | ML | MIVQUE0 | TYPE1 | TYPE2 | TYPE3
-
specifies the estimation method for the covariance parameters. The
REML specification performs residual (restricted) maximum likelihood, and it is the default method. The ML specification performs
maximum likelihood, and the MIVQUE0 specification performs minimum variance quadratic unbiased estimation of the covariance
parameters.
The METHOD=TYPEn specifications apply only to variance component models with no SUBJECT=
effects and no REPEATED
statement. An analysis of variance table is included in the output, and the expected mean squares are used to estimate the
variance components (see Chapter 46: The GLM Procedure, for further explanation). The resulting method-of-moment variance component estimates are used in subsequent calculations,
including standard errors computed from ESTIMATE
and LSMEANS
statements. The ODS table names are Type1, Type2, and Type3, respectively.
-
MMEQ
-
requests that the coefficient matrix and the right-hand side of the
mixed model equations be displayed. If 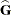 is nonsingular, the coefficient matrix and the right-hand side have the following form:
is nonsingular, the coefficient matrix and the right-hand side have the following form:
If 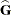 is singular, the coefficient matrix and right-hand side have the following modified form:
is singular, the coefficient matrix and right-hand side have the following modified form:
See the section Estimating Fixed and Random Effects in the Mixed Model for further information about these equations.
-
MMEQSOL
-
requests that a solution to the mixed model equations be produced,
in addition to the inverted coefficients matrix. If 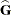 is nonsingular, the formula is the same as the preceding description of the MMEQ
option. If
is nonsingular, the formula is the same as the preceding description of the MMEQ
option. If 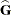 is singular,
is singular, 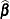 and
and 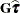 are displayed in addition to the inverse of the modified coefficient matrix.
are displayed in addition to the inverse of the modified coefficient matrix.
See the section Estimating Fixed and Random Effects in the Mixed Model for further information about these equations and solution transformation.
-
NAMELEN<=number>
-
specifies the length to which long effect names are shortened.
The default and minimum value is 20.
-
NOBOUND
-
has the same effect as the NOBOUND
option in the PARMS
statement.
-
NOCLPRINT<=number>
-
suppresses the display of the "Class Level Information" table
if you do not specify number. If you do specify number, only levels with totals that are less than number are listed in the table.
-
NOINFO
-
suppresses the display of the "Model Information,"
"Dimensions," and "Number of Observations" tables.
-
NOITPRINT
-
suppresses the display of the "Iteration History" table.
-
NOPROFILE
-
includes the residual variance as part of the Newton-Raphson
iterations. This option applies only to models that have a residual variance parameter. By default, this parameter is profiled
out of the likelihood calculations, except when you have specified the HOLD=
option in the PARMS
statement.
-
ORD
-
displays ordinates of the relevant distribution in addition to
p-values. The ordinate can be viewed as an approximate odds ratio of hypothesis probabilities.
-
ORDER=DATA | FORMATTED | FREQ | INTERNAL
-
specifies the sort order for the levels of the classification variables (which are specified in the CLASS
statement).
This option applies to the levels for all classification variables, except when you use the (default) ORDER=FORMATTED option
with numeric classification variables that have no explicit format. In that case, the levels of such variables are ordered
by their internal value.
The ORDER= option can take the following values:
|
Value of ORDER=
|
Levels Sorted By
|
|
DATA
|
Order of appearance in the input data set
|
|
FORMATTED
|
External formatted value, except for numeric variables with no explicit format, which are sorted by their unformatted (internal)
value
|
|
FREQ
|
Descending frequency count; levels with the most observations come first in the order
|
|
INTERNAL
|
Unformatted value
|
By default, ORDER=FORMATTED. For ORDER=FORMATTED and ORDER=INTERNAL, the sort order is machine-dependent.
For more information about sort order, see the chapter on the SORT procedure in the
Base SAS Procedures Guide and the discussion of BY-group processing in
SAS Language Reference: Concepts.
-
PLOTS <(global-plot-options )> <=plot-request <(options )>>
PLOTS <(global-plot-options )> <= (plot-request<(options)> <…plot-request<(options)> >)>
-
requests that the MIXED procedure produce statistical graphics via
the Output Delivery System, provided that ODS Graphics is enabled.
ODS Graphics must be enabled before plots can be requested. For example:
ods graphics on;
proc mixed data=heights plots=all;
class Family Gender;
model Height = Gender / residual;
random Family Family*Gender;
run;
ods graphics off;
For more information about enabling and disabling ODS Graphics, see the section Enabling and Disabling ODS Graphics in Chapter 21: Statistical Graphics Using ODS.
For examples of the basic statistical graphics produced by the MIXED procedure and aspects of their computation and interpretation,
see the section ODS Graphics.
The global-plot-options apply to all relevant plots generated by the MIXED procedure. The global-plot-options supported by the MIXED procedure follow.
Global Plot Options
-
OBSNO
-
uses the data set observation number to identify observations in tooltips, provided that the observation number can be determined.
Otherwise, the number displayed in tooltips is the index of the observation as it is used in the analysis within the BY group.
-
ONLY
-
suppresses the default plots. Only the plots specifically requested are produced.
-
UNPACKPANEL
UNPACK
-
displays each graph separately. (By default, some graphs can appear together in a single panel.)
-
MAXPOINTS=NONE | number
-
specifies that plots with elements that require processing more than number points be suppressed. The default is MAXPOINTS=5000. No plots are suppressed if you specify MAXPOINTS=NONE.
Specific Plot Options
The following listing describes the specific plots and their options.
-
ALL
-
requests that all plots appropriate for the particular analysis be produced.
-
BOXPLOT <(boxplot-options)>
-
requests box plots for the effects in your model that consist of classification effects only. Note that these effects can
involve more than one classification variable (interaction and nested effects), but they cannot contain any continuous variables.
By default, the BOXPLOT request produces box plots based on (conditional) raw residuals for the qualifying effects in the
MODEL
, RANDOM
, and REPEATED
statements. See the discussion of the boxplot-options in a later section for information about how to tune your box plot request.
-
DISTANCE<(USEINDEX)>
-
requests a plot of the likelihood or restricted likelihood distance. When influence diagnostics are requested with set selection
according to an effect, the USEINDEX option enables you to replace the formatted tick values on the horizontal axis with integer
indices of the effect levels in order to reduce the space taken up by the horizontal plot axis.
-
INFLUENCEESTPLOT<(options)>
-
requests panels of the deletion estimates in an influence analysis, provided that the INFLUENCE
option is specified in the MODEL
statement. No plots are produced for fixed-effects parameters associated with singular columns in the 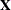 matrix or for covariance parameters associated with singularities in the ASYCOV
matrix. By default, separate panels are produced for the fixed-effects and covariance parameters delete estimates. The FIXED
and RANDOM options enable you to select these specific panels. The UNPACK option produces separate plots for each of the parameter
estimates. The USEINDEX option replaces formatted tick values for the horizontal axis with integer indices.
matrix or for covariance parameters associated with singularities in the ASYCOV
matrix. By default, separate panels are produced for the fixed-effects and covariance parameters delete estimates. The FIXED
and RANDOM options enable you to select these specific panels. The UNPACK option produces separate plots for each of the parameter
estimates. The USEINDEX option replaces formatted tick values for the horizontal axis with integer indices.
-
INFLUENCESTATPANEL<(options)>
-
requests panels of influence statistics. For iterative influence analysis (see the INFLUENCE
option in the MODEL
statement), the panel shows the Cook’s D and CovRatio statistics for fixed-effects and covariance parameters, enabling you to gauge impact on estimates and precision
for both types of estimates. In noniterative analysis, only statistics for the fixed effects are plotted. The UNPACK option
produces separate plots from the elements in the panel. The USEINDEX option replaces formatted tick values for the horizontal
axis with integer indices.
-
RESIDUALPANEL <(residual-plot-options)>
-
requests a panel of raw residuals. By default, the conditional residuals are produced. See the discussion of residual-plot-options in a later section for information about how to tune this panel.
-
STUDENTPANEL <(residual-plot-options)>
-
requests a panel of studentized residuals. By default, the conditional residuals are produced. See the discussion of residual-plot-options in a later section for information about how to tune this panel.
-
PEARSONPANEL <(residual-plot-options)>
-
requests a panel of Pearson residuals. By default, the conditional residuals are produced. See the discussion of residual-plot-options in a later section for information about how to tune this panel.
-
PRESS<(USEINDEX)>
-
requests a plot of PRESS residuals or PRESS statistics. These are based on "leave-one-out" or "leave-set-out" prediction of
the marginal mean. When influence diagnostics are requested with set selection according to an effect, the USEINDEX option
enables you to replace the formatted tick values on the horizontal axis with integer indices of the effect levels in order
to reduce the space taken up by the horizontal plot axis.
-
VCIRYPANEL <(residual-plot-options)>
-
requests a panel of residual graphics based on the scaled residuals. See the VCIRY
option in the MODEL
statement for details about these scaled residuals. Only the UNPACK and BOX options of the residual-plot-options are available for this type of residual panel.
-
NONE
-
suppresses all plots.
Residual Plot Options
The residual-plot-options determine both the composition of the panels and the type of residuals being plotted.
-
BOX
BOXPLOT
-
replaces the inset of summary statistics in the lower-right corner of the panel with a box plot of the residual (the "PROC
GLIMMIX look").
-
CONDITIONAL
BLUP
-
constructs plots from conditional residuals.
-
MARGINAL
NOBLUP
-
constructs plots from marginal residuals.
-
UNPACK
-
produces separate plots from the elements of the panel. The inset statistics are not part of the unpack operation.
Box Plot Options
The boxplot-options determine whether box plots are produced for residuals or for residuals and observed values, and for which model effects
the box plots are constructed. The available boxplot-options are as follows.
-
CONDITIONAL
BLUP
-
constructs box plots from conditional residuals—that is, residuals using the estimated BLUPs of random effects.
-
FIXED
-
produces box plots for all fixed effects (MODEL
statement) consisting entirely of classification variables
-
GROUP
-
produces box plots for all GROUP= effects (RANDOM
and REPEATED
statement) consisting entirely of classification variables
-
MARGINAL
NOBLUP
-
constructs box plots from marginal residuals.
-
NPANEL=number
-
provides the ability to break a box plot into multiple graphics. If number is negative, no balancing of the number of boxes takes place and number is the maximum number of boxes per graphic. If number is positive, the number of boxes per graphic is balanced. For example, suppose variable A has 125 levels, and consider the following statements:
ods graphics on;
proc mixed plots=boxplot(npanel=20);
class A;
model y = A;
run;
The box balancing results in six plots with 18 boxes each and one plot with 17 boxes. If number is zero, and this is the default, all levels of the effect are displayed in a single plot.
-
OBSERVED
-
adds box plots of the observed data for the selected effects.
-
RANDOM
-
produces box plots for all random effects (RANDOM
statement) consisting entirely of classification variables. This does not include effects specified in the GROUP=
or SUBJECT=
options of the RANDOM
statement.
-
REPEATED
-
produces box plots for the repeated effects (REPEATED
statement). This does not include effects specified in the GROUP=
or SUBJECT=
options of the REPEATED
statement.
-
STUDENT
-
constructs box plots from studentized residuals rather than from raw residuals.
-
SUBJECT
-
produces box plots for all SUBJECT= effects (RANDOM
and REPEATED
statement) consisting entirely of classification variables.
-
USEINDEX
-
uses as the horizontal axis label the index of the effect level rather than the formatted value(s). For classification variables
with many levels or model effects that involve multiple classification variables, the formatted values identifying the effect
levels can take up too much space as axis tick values, leading to extensive thinning. The USEINDEX option replaces tick values
constructed from formatted values with the internal level number.
Multiple Plot Requests
You can list a plot request one or more times with different options. For example, the following statements request a panel
of marginal raw residuals, individual plots generated from a panel of the conditional raw residuals, and a panel of marginal
studentized residuals:
ods graphics on;
proc mixed plots(only)=(
ResidualPanel(marginal)
ResidualPanel(unpack conditional)
StudentPanel(marginal box));
The inset of residual statistics is replaced in this last panel by a box plot of the studentized residuals. Similarly, if
you specify the INFLUENCE
option in the MODEL
statement, then the following statements request statistical graphics of fixed-effects deletion estimates (in a panel), covariance
parameter deletion estimates (unpacked in individual plots), and box plots for the SUBJECT= and fixed classification effects
based on residuals and observed values:
ods graphics on / imagefmt=staticmap;
proc mixed plots(only)=(
InfluenceEstPlot(fixed)
InfluenceEstPlot(random unpack)
BoxPlot(observed fixed subject));
The STATICMAP image format enables tooltips that show, for example, values of influence diagnostics associated with a particular
delete estimate.
This concludes the syntax section for the PLOTS=
option in the PROC MIXED
statement.
-
RANKS
-
displays the ranks of design matrices
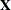 and (
and (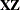 ).
).
-
RATIO
-
produces the ratio of the covariance parameter estimates to
the estimate of the residual variance when the latter exists in the model.
-
RIDGE=number
-
specifies the starting value for the minimum ridge value
used in the Newton-Raphson algorithm. The default is 0.3125.
-
SCORING<=number>
-
requests that Fisher scoring be used in association with the
estimation method up to iteration number, which is 0 by default. When you use the SCORING= option and PROC MIXED converges without stopping the scoring algorithm,
PROC MIXED uses the expected Hessian matrix to compute approximate standard errors for the covariance parameters instead of
the observed Hessian. The output from the ASYCOV
and ASYCORR
options is similarly adjusted.
-
SIGITER
-
is an alias for the NOPROFILE
option.
-
UPDATE
-
is an alias for the LOGNOTE
option.

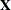
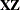
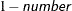
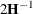
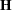
![\[ \frac{\nu \widehat{\sigma }^2}{\chi ^2_{\nu ,1-\alpha /2}} \leq \sigma ^2 \leq \frac{\nu \widehat{\sigma }^2}{\chi ^2_{\nu ,\alpha /2}} \]](images/statug_mixed0029.png)
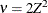
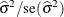
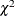

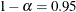
![\[ \frac{|f_ k - f_{k-1}|}{|f_ k|} \leq \Argument{number} \]](images/statug_mixed0035.png)
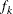
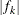
![\[ \frac{\mr{max} _ j |g_{jk}|}{|f_ k|} \leq \Argument{number} \]](images/statug_mixed0038.png)
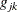
![\[ \frac{{\mb{g}_ k}' \mb{H} ^{-1}_ k{\mb{g}_ k}}{|f_ k|} \leq \Argument{number} \]](images/statug_mixed0040.png)
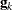
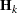
![\[ \frac{\mb{g}_ k'\mb{g}_ k}{|f_ k|} \leq \Argument{number} \]](images/statug_mixed0043.png)
![\[ (\mb{X}’\widehat{\mb{V}}^{-1}\mb{X})^- \left(\sum _{i=1}^ S \mb{X}_ i’\widehat{\mb{V}_ i}^{-1} \widehat{\bepsilon _ i} \widehat{\bepsilon _ i}’ \widehat{\mb{V}_ i}^{-1}\mb{X}_ i \right) (\mb{X}’\widehat{\mb{V}}^{-1}\mb{X})^- \]](images/statug_mixed0044.png)
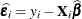
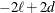
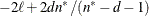
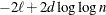
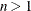
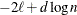
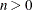
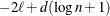
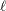
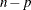
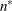
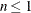
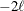
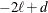
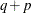
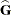
![\[ \left[\begin{array}{lr} \bX ’\widehat{\bR }^{-1}\bX & \bX ’\widehat{\bR }^{-1}\bZ \\*\bZ ’\widehat{\bR }^{-1}\bX & \bZ ’\widehat{\bR }^{-1}\bZ + \widehat{\bG }^{-1} \end{array}\right] \left[\begin{array}{c} \widehat{\bbeta } \\ \widehat{\bgamma } \end{array} \right] = \left[\begin{array}{c} \bX ’\widehat{\bR }^{-1}\mb{y} \\ \bZ ’\widehat{\bR }^{-1}\mb{y} \end{array} \right] \]](images/statug_mixed0061.png)
![\[ \left[\begin{array}{lr} \bX ’\widehat{\bR } ^{-1}\bX & \bX ’\widehat{\bR } ^{-1} \bZ \widehat{\bG } \\*\widehat{\bG }’\bZ ’\widehat{\bR } ^{-1}\bX & \widehat{\bG }’\bZ ’\widehat{\bR } ^{-1}\bZ \widehat{\bG } + \bG \end{array}\right] \left[\begin{array}{c} \widehat{\bbeta } \\ \widehat{\btau } \end{array} \right] = \left[\begin{array}{r} \bX ’\widehat{\bR } ^{-1}\mb{y} \\ \widehat{\bG }’\bZ ’\widehat{\bR } ^{-1}\mb{y} \end{array} \right] \]](images/statug_mixed0062.png)