The MCMC Procedure
-
Overview

-
Getting Started

-
Syntax

-
Details
 How PROC MCMC Works Blocking of Parameters Sampling Methods Tuning the Proposal Distribution Conjugate Sampling Initial Values of the Markov Chains Assignments of Parameters Standard Distributions Usage of Multivariate Distributions Specifying a New Distribution Using Density Functions in the Programming Statements Truncation and Censoring Some Useful SAS Functions Matrix Functions in PROC MCMC Create Design Matrix Modeling Joint Likelihood Regenerating Diagnostics Plots Caterpillar Plot Posterior Predictive Distribution Handling of Missing Data Floating Point Errors and Overflows Handling Error Messages Computational Resources Displayed Output ODS Table Names ODS Graphics
How PROC MCMC Works Blocking of Parameters Sampling Methods Tuning the Proposal Distribution Conjugate Sampling Initial Values of the Markov Chains Assignments of Parameters Standard Distributions Usage of Multivariate Distributions Specifying a New Distribution Using Density Functions in the Programming Statements Truncation and Censoring Some Useful SAS Functions Matrix Functions in PROC MCMC Create Design Matrix Modeling Joint Likelihood Regenerating Diagnostics Plots Caterpillar Plot Posterior Predictive Distribution Handling of Missing Data Floating Point Errors and Overflows Handling Error Messages Computational Resources Displayed Output ODS Table Names ODS Graphics -
Examples
 Simulating Samples From a Known Density Box-Cox Transformation Logistic Regression Model with a Diffuse Prior Logistic Regression Model with Jeffreys’ Prior Poisson Regression Nonlinear Poisson Regression Models Logistic Regression Random-Effects Model Nonlinear Poisson Regression Random-Effects Model Multivariate Normal Random-Effects Model Change Point Models Exponential and Weibull Survival Analysis Time Independent Cox Model Time Dependent Cox Model Piecewise Exponential Frailty Model Normal Regression with Interval Censoring Constrained Analysis Implement a New Sampling Algorithm Using a Transformation to Improve Mixing Gelman-Rubin Diagnostics
Simulating Samples From a Known Density Box-Cox Transformation Logistic Regression Model with a Diffuse Prior Logistic Regression Model with Jeffreys’ Prior Poisson Regression Nonlinear Poisson Regression Models Logistic Regression Random-Effects Model Nonlinear Poisson Regression Random-Effects Model Multivariate Normal Random-Effects Model Change Point Models Exponential and Weibull Survival Analysis Time Independent Cox Model Time Dependent Cox Model Piecewise Exponential Frailty Model Normal Regression with Interval Censoring Constrained Analysis Implement a New Sampling Algorithm Using a Transformation to Improve Mixing Gelman-Rubin Diagnostics - References
Example 54.8 Nonlinear Poisson Regression Random-Effects Model
This example uses the pump failure data of Gaver and O’Muircheartaigh (1987). The number of failures and the time of operation are recorded for 10 pumps. Each of the pumps is classified into one of two groups corresponding to either continuous or intermittent operation. The following statements generate the data set:
title 'Nonlinear Poisson Regression Random-Effects Model'; data pump; input y t group @@; pump = _n_; logtstd = log(t) - 2.4564900; datalines; 5 94.320 1 1 15.720 2 5 62.880 1 14 125.760 1 3 5.240 2 19 31.440 1 1 1.048 2 1 1.048 2 4 2.096 2 22 10.480 2 ;
Each row denotes data for a single pump, and the variable logtstd contains the centered operation times. Letting  denote the number of failures for the
denote the number of failures for the 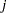 th pump in the
th pump in the  th group, Draper (1996) considers the following hierarchical model for these data:
th group, Draper (1996) considers the following hierarchical model for these data:
 |
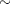 |
 |
|||
 |
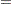 |
 |
The model specifies different intercepts and slopes for each group, and the random effect 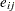 is a mechanism for accounting for overdispersion. You can use noninformative priors on the parameters
is a mechanism for accounting for overdispersion. You can use noninformative priors on the parameters  ,
,  , and
, and 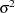 , and normal prior on
, and normal prior on 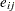 :
:
 |
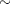 |
 |
|||
 |
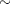 |
 |
|||
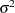 |
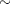 |
 |
|||
 |
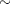 |
 |
The following statements fit this nonlinear hierarchical model and produce Output 54.8.1:
ods graphics on; proc mcmc data=pump outpost=postout seed=248601 nmc=10000 plots=trace stats=none diag=none; ods select tracepanel; parms s2; prior s2 ~ igamma(0.01, scale=0.01); random alpha ~ normal(0, sd=1000) subject=group monitor=(alpha); random beta ~ normal(0, sd=1000) subject=group monitor=(beta); random e ~ normal(0, var=s2) subject=pump; w = alpha + beta * logtstd + e; lambda = exp(w); model y ~ poisson(lambda); run;
The PROC MCMC statement specifies the input data set (Pump), the output data set (Postout), a seed for the random number generator, and an MCMC sample of 10,000. The program requests that only trace plots be produced. The program also requests that posterior calculations and convergence diagnostics tests be disabled. The ODS SELECT statement displays the trace plots, and that is the primary focus.
There is only one model parameter, the variance s2 in the prior distribution for the random effect 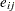 . The three following RANDOM statements specify random intercepts (alpha), random slopes (beta), and observationwise random effect e. The SUBJECT= option indicates the group indices for each random effect. The MONITOR= option selects the random-effects parameters of interest.
. The three following RANDOM statements specify random intercepts (alpha), random slopes (beta), and observationwise random effect e. The SUBJECT= option indicates the group indices for each random effect. The MONITOR= option selects the random-effects parameters of interest.
Next, programming statements construct the mean of the Poisson likelihood, and the MODEL statement specifies the likelihood function for each observation.
Output 54.8.1 shows trace plots for the variance parameter 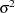 and the random-effects parameters
and the random-effects parameters  and
and  . You can see that the chains are mixing poorly.
. You can see that the chains are mixing poorly.
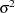 ,
,  , and
, and 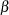 without Hierarchical Centering
without Hierarchical Centering


To improve mixing, you can repeat the same analysis by using a hierarchical centering technique, where instead of using a normal prior centered at 0 on 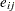 , you center the random effects on the group means:
, you center the random effects on the group means:
 |
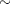 |
 |
|||
 |
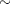 |
 |
Because PROC MCMC does not allow random effects to be in the prior distribution of another random effect, you cannot use the following syntax:
random alpha ~ normal(0, sd=1000) subject=group; random beta ~ normal(0, sd=1000) subject=group; w = alpha + beta * logtstd; random llambda ~ normal(w, var=s2) subject=pump;
You have to allocate arrays for the upper-level random effects  and
and  and treat them as model parameters by declaring them in the PARMS statements. The following program illustrates how to fit a multilevel hierarchical centering random-effects model:
and treat them as model parameters by declaring them in the PARMS statements. The following program illustrates how to fit a multilevel hierarchical centering random-effects model:
proc mcmc data=pump outpost=postout_c seed=248601 nmc=10000 plots=trace; ods select tracepanel postsummaries postintervals; array alpha[2]; array beta[2]; parms (alpha: beta:) 1 s2 1; prior alpha: beta: ~ normal(0, sd=1000); prior s2 ~ igamma(0.01, scale=0.01); w = alpha[group] + beta[group] * logtstd; random llambda ~ normal(w, var = s2) subject=pump; lambda = exp(llambda); model y ~ poisson(lambda); run;
The difference between this program and the previous one is that alpha and beta are no longer declared as random effects in the RANDOM statements. Instead, you use ARRAY statements to allocate two arrays of size 2: one for alpha and one for beta. They are now treated as model parameters. You use the PARMS statement to declare the model parameters, and you use PRIOR statements to specify the prior distribuions. The symbol w is the mean of the normal distribution for the random effect llambda. Note that the data set variable group is used in alpha[group] and beta[group] as a way to select the appropriate intercept and slope for each random effect llambda.
The symbol lambda is the exponential of the corresponding  (llambda), and the MODEL statement gives the response variable y a Poisson likelihood with a mean parameter lambda, in the same manner as you saw previously.
(llambda), and the MODEL statement gives the response variable y a Poisson likelihood with a mean parameter lambda, in the same manner as you saw previously.
The trace plots of 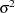 ,
,  , and
, and  are shown in Output 54.8.2. The mixing is significantly improved over the previous model. The posterior summary and interval statistics tables are shown in Output 54.8.1.
are shown in Output 54.8.2. The mixing is significantly improved over the previous model. The posterior summary and interval statistics tables are shown in Output 54.8.1.
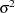 ,
,  , and
, and 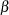 with Hierarchical Centering
with Hierarchical Centering


| Nonlinear Poisson Regression Random-Effects Model |
| Posterior Summaries | ||||||
|---|---|---|---|---|---|---|
| Parameter | N | Mean | Standard Deviation |
Percentiles | ||
| 25% | 50% | 75% | ||||
| alpha1 | 10000 | 2.9155 | 2.4284 | 1.4939 | 2.9239 | 4.1783 |
| alpha2 | 10000 | 1.6013 | 0.8997 | 1.0924 | 1.6570 | 2.1848 |
| beta1 | 10000 | -0.4282 | 1.3216 | -1.1022 | -0.4104 | 0.3000 |
| beta2 | 10000 | 0.5612 | 0.6271 | 0.2086 | 0.5753 | 0.9304 |
| s2 | 10000 | 1.7926 | 2.0767 | 0.7231 | 1.1842 | 2.0505 |
| Posterior Intervals | |||||
|---|---|---|---|---|---|
| Parameter | Alpha | Equal-Tail Interval | HPD Interval | ||
| alpha1 | 0.050 | -2.0883 | 8.2255 | -2.1392 | 7.9537 |
| alpha2 | 0.050 | -0.2379 | 3.1588 | -0.2082 | 3.1653 |
| beta1 | 0.050 | -3.3218 | 2.3148 | -3.0057 | 2.5151 |
| beta2 | 0.050 | -0.6950 | 1.8336 | -0.6555 | 1.8502 |
| s2 | 0.050 | 0.3051 | 7.3173 | 0.1287 | 5.2457 |
You can easily generate a caterpillar plot (Output 54.8.4) of the random-effects parameters by calling the %CATER macro:
%CATER(data=postout_c, var=llambda_:); ods graphics off;
Varying llambda indicates nonconstant dispersion in the Poisson model.
