The MCMC Procedure
-
Overview

-
Getting Started

-
Syntax

-
Details
 How PROC MCMC Works Blocking of Parameters Sampling Methods Tuning the Proposal Distribution Conjugate Sampling Initial Values of the Markov Chains Assignments of Parameters Standard Distributions Usage of Multivariate Distributions Specifying a New Distribution Using Density Functions in the Programming Statements Truncation and Censoring Some Useful SAS Functions Matrix Functions in PROC MCMC Create Design Matrix Modeling Joint Likelihood Regenerating Diagnostics Plots Caterpillar Plot Posterior Predictive Distribution Handling of Missing Data Floating Point Errors and Overflows Handling Error Messages Computational Resources Displayed Output ODS Table Names ODS Graphics
How PROC MCMC Works Blocking of Parameters Sampling Methods Tuning the Proposal Distribution Conjugate Sampling Initial Values of the Markov Chains Assignments of Parameters Standard Distributions Usage of Multivariate Distributions Specifying a New Distribution Using Density Functions in the Programming Statements Truncation and Censoring Some Useful SAS Functions Matrix Functions in PROC MCMC Create Design Matrix Modeling Joint Likelihood Regenerating Diagnostics Plots Caterpillar Plot Posterior Predictive Distribution Handling of Missing Data Floating Point Errors and Overflows Handling Error Messages Computational Resources Displayed Output ODS Table Names ODS Graphics -
Examples
 Simulating Samples From a Known Density Box-Cox Transformation Logistic Regression Model with a Diffuse Prior Logistic Regression Model with Jeffreys’ Prior Poisson Regression Nonlinear Poisson Regression Models Logistic Regression Random-Effects Model Nonlinear Poisson Regression Random-Effects Model Multivariate Normal Random-Effects Model Change Point Models Exponential and Weibull Survival Analysis Time Independent Cox Model Time Dependent Cox Model Piecewise Exponential Frailty Model Normal Regression with Interval Censoring Constrained Analysis Implement a New Sampling Algorithm Using a Transformation to Improve Mixing Gelman-Rubin Diagnostics
Simulating Samples From a Known Density Box-Cox Transformation Logistic Regression Model with a Diffuse Prior Logistic Regression Model with Jeffreys’ Prior Poisson Regression Nonlinear Poisson Regression Models Logistic Regression Random-Effects Model Nonlinear Poisson Regression Random-Effects Model Multivariate Normal Random-Effects Model Change Point Models Exponential and Weibull Survival Analysis Time Independent Cox Model Time Dependent Cox Model Piecewise Exponential Frailty Model Normal Regression with Interval Censoring Constrained Analysis Implement a New Sampling Algorithm Using a Transformation to Improve Mixing Gelman-Rubin Diagnostics - References
| Standard Distributions |
The section Univariate Distributions (Table 54.7 through Table 54.34) lists all univariate distributions that PROC MCMC recognizes. The section Multivariate Distributions (Table 54.35 through Table 54.38) lists all multivariate distributions that PROC MCMC recognizes. With the exception of the multinomial distribution, all these distributions can be used in the MODEL, PRIOR, and HYPERPRIOR statements. The multinomial distribution is supported only in the MODEL statement. The RANDOM statement supports a limited number of distributions; see Table 54.4 for the complete list.
See the section Using Density Functions in the Programming Statements for information about how to use distributions in the programming statements. To specify an arbitrary distribution, you can use the GENERAL and DGENERAL functions. See the section Specifying a New Distribution for more details. See the section Truncation and Censoring for tips about how to work with truncated distributions and censoring data.
Univariate Distributions
PROC specification |
beta( |
Density |
|
Parameter restriction |
|
Range |
|
Mean |
|
Variance |
|
Mode |
|
Random number |
If |
PROC specification |
binary( |
Density |
|
Parameter restriction |
|
Range |
|
Mean |
round |
Variance |
|
Mode |
|
Random number |
Generate |
PROC specification |
binomial( |
Density |
|
Parameter restriction |
|
Range |
|
Mean |
|
Variance |
|
Mode |
|
PROC specification |
cauchy( |
Density |
|
Parameter restriction |
|
Range |
|
Mean |
Does not exist. |
Variance |
Does not exist. |
Mode |
|
Random number |
Generate |
PROC specification |
chisq( |
Density |
|
Parameter restriction |
|
Range |
|
Mean |
|
Variance |
|
Mode |
|
Random number |
|
PROC specification |
expchisq( |
Density |
|
Parameter restriction |
|
Range |
|
Mode |
|
Random number |
Generate |
Relationship to the |
|
PROC specification |
expexpon(scale = |
expexpon(iscale = |
Density |
|
|
Parameter restriction |
|
|
Range |
|
Same |
Mode |
|
|
Random number |
Generate |
|
Relationship to the exponential distribution |
|
|
PROC specification |
expgamma( |
expgamma( |
Density |
|
|
Parameter restriction |
|
|
Range |
|
Same |
Mode |
|
|
Random number |
Generate |
|
Relationship to the |
|
|
PROC specification |
expichisq( |
Density |
|
Parameter restriction |
|
Range |
|
Mode |
|
Random number |
Generate |
Relationship to the |
|
PROC specification |
expigamma( |
expigamma( |
Density |
|
|
Parameter restriction |
|
|
Range |
|
Same |
Mode |
|
|
Random number |
Generate |
|
Relationship to the |
|
|
PROC specification |
expsichisq( |
Density |
|
Parameter restriction |
|
Range |
|
Mode |
|
Random number |
Generate |
Relationship to the |
|
PROC specification |
expon(scale = |
expon(iscale = |
Density |
|
|
Parameter restriction |
|
|
Range |
|
Same |
Mean |
|
|
Variance |
|
|
Mode |
|
|
Random number |
The exponential distribution is a special case of the gamma distribution: |
|
PROC specification |
gamma( |
gamma( |
Density |
|
|
Parameter restriction |
|
|
Range |
|
Same |
Mean |
|
|
Variance |
|
|
Mode |
|
|
Random number |
See (McGrath and Irving; 1973). |
|
PROC specification |
geo( |
Density 1 |
|
Parameter restriction |
|
Range |
|
Mean |
round( |
Variance |
|
Mode |
|
Random number |
Based on samples obtained from a Bernoulli distribution with probability |
PROC specification |
ichisq( |
Density |
|
Parameter restriction |
|
Range |
|
Mean |
|
Variance |
|
Mode |
|
Random number |
Inverse |
PROC specification |
igamma( |
igamma( |
Density |
|
|
Parameter restriction |
|
|
Range |
|
Same |
Mean |
|
|
Variance |
|
|
Mode |
|
|
Random number |
Generate |
|
Relationship to the gamma distribution |
|
|
PROC specification |
laplace( |
laplace( |
Density |
|
|
Parameter restriction |
|
|
Range |
|
Same |
Mean |
|
|
Variance |
|
|
Mode |
|
|
Random number |
Inverse CDF. |
|
PROC specification |
logistic( |
Density |
|
Parameter restriction |
|
Range |
|
Mean |
|
Variance |
|
Mode |
|
Random number |
Inverse CDF method with |
PROC specification |
lognormal( |
lognormal( |
lognormal( |
Density |
|
|
|
Parameter restriction |
|
|
|
Range |
|
Same |
Same |
Mean |
|
|
|
Variance |
|
|
|
Mode |
|
|
|
Random number |
Generate |
||
PROC specification |
negbin( |
Density |
|
Parameter restriction |
|
Range |
|
Mean |
round |
Variance |
|
Mode |
|
Random number |
Generate |
PROC specification |
normal( |
normal( |
normal( |
Density |
|
|
|
Parameter restriction |
|
|
|
Range |
|
Same |
Same |
Mean |
|
Same |
Same |
Variance |
|
|
|
Mode |
|
Same |
Same |
PROC specification |
pareto( |
Density |
|
Parameter restriction |
|
Range |
|
Mean |
|
Variance |
|
Mode |
|
Random number |
Inverse CDF method with |
Useful transformation |
|
PROC specification |
poisson( |
Density |
|
Parameter restriction |
|
Range |
|
Mean |
|
Variance |
|
Mode |
round |
PROC specification |
sichisq( |
Density |
|
Parameter restriction |
|
Range |
|
Mean |
|
Variance |
|
Mode |
|
Random number |
Scaled inverse |
PROC specification |
t( |
t( |
t( |
Density |
|
|
|
Parm restriction |
|
|
|
Range |
|
Same |
Same |
Mean |
|
Same |
Same |
Variance |
|
|
|
Mode |
|
Same |
Same |
Random number |
|
||
PROC specification |
uniform( |
Density |
|
Parameter restriction |
none |
Range |
|
Mean |
|
Variance |
|
Mode |
Does not exist |
Random number |
Mersenne Twister (Matsumoto and Kurita; 1992, 1994; Matsumoto and Nishimura; 1998) |
PROC specification |
wald( |
Density |
|
Parameter restriction |
|
Range |
|
Mean |
|
Variance |
|
Mode |
|
Random number |
Generate |
PROC specification |
weibull( |
Density |
|
Parameter restriction |
|
Range |
|
Mean |
|
Variance |
|
Mode |
|
Random number |
Inverse CDF method with |
Multivariate Distributions
PROC specification |
|
Density |
|
Parameter restriction |
|
Range |
|
Mean |
|
Mode |
|
PROC specification |
|
Density |
|
Parameter restriction |
|
Range |
|
Mean |
|
Mode |
|
PROC specification |
|
Density |
|
Parameter restriction |
|
Range |
|
Mean |
|
Mode |
|
PROC specification |
|
Density |
|
Parameter restriction |
|
Range |
|
Mean |
|
 ,
, 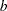 )
) 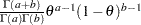
 ,
, 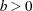
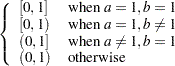
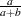
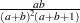
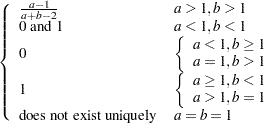
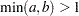 , see
, see 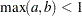 , see
, see  and
and 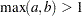 , see
, see 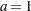 or
or 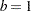 , use the inversion method; if
, use the inversion method; if  , use a uniform random number generator.
, use a uniform random number generator.  )
) 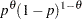
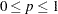
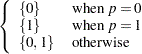
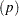
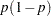
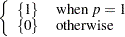
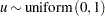 . If
. If 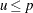 ,
, 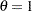 ; else,
; else, 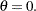
 ,
, 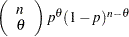
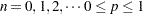
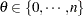
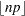

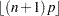
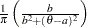
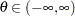

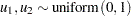 ; let
; let  . Repeat the procedure until
. Repeat the procedure until 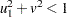 .
. 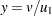 is a draw from the standard Cauchy, and
is a draw from the standard Cauchy, and 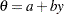
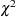 Distribution
Distribution )
) 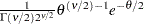
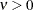
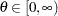 if
if 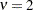 ;
; 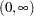 otherwise.
otherwise. 
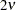
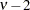 if
if 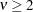 ; does not exist otherwise.
; does not exist otherwise. 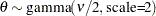 is a draw from the
is a draw from the 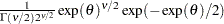
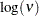
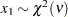 , and
, and 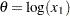 is a draw from the exponential
is a draw from the exponential 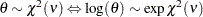
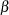 )
) 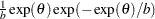

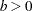
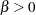
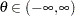

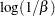
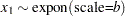 , and
, and 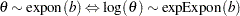
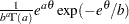
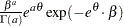
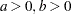
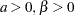
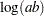
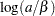
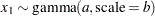 , and
, and 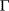 distribution
distribution 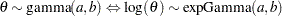
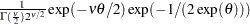
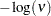
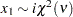 , and
, and 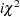 distribution
distribution 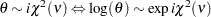

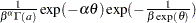
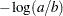
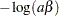
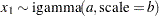 , and
, and 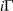 distribution
distribution 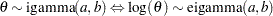
 )
) 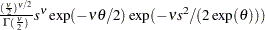
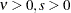
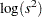
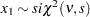 , and
, and 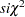 distribution
distribution 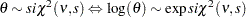
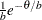
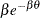
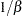
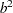
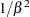
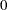
 is a draw from the exponential distribution.
is a draw from the exponential distribution. 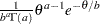
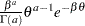
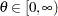 if
if 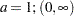 otherwise.
otherwise. 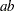

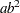
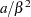
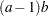 if
if 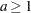
 if
if 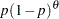
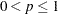
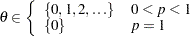
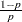 )
) 
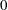
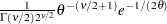
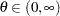
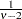 if
if 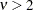
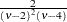 if
if 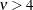
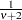
 is a draw from the inverse
is a draw from the inverse 
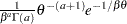
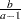 if
if 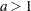
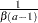 if
if 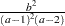
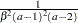
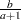

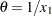 is a draw from the
is a draw from the  distribution.
distribution. 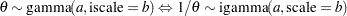
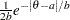
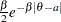
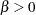
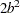
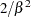
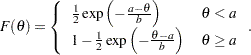
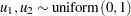 . If
. If  else
else 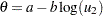 .
.  is a draw from the Laplace distribution.
is a draw from the Laplace distribution. 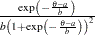
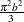
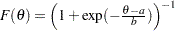 . Generate
. Generate 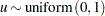 , and
, and 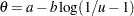 is a draw from the logistic distribution.
is a draw from the logistic distribution. 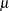 ,
,  )
)  )
) 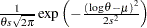
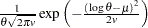
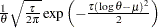
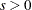

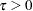
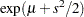

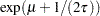
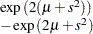
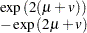
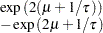

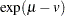
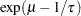
 , and
, and 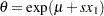 is a draw from the lognormal distribution.
is a draw from the lognormal distribution. 
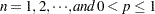
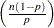
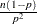
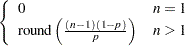
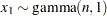 , and
, and 
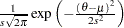
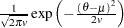
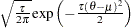
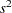
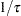
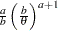
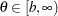
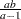 if
if 
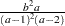
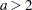
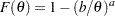 . Generate
. Generate 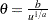 is a draw from the Pareto distribution.
is a draw from the Pareto distribution. 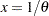 is Beta(
is Beta(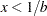 }.
}. 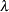 )
) 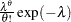
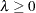
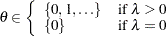
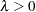
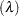
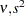 )
) 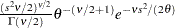
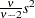 if
if 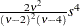 if
if 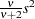
 is a draw from the scaled inverse
is a draw from the scaled inverse 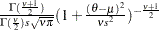
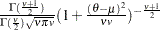
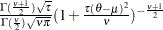
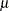 if
if 
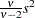 if
if 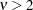
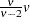 if
if 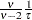 if
if 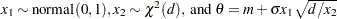 is a draw from the t distribution.
is a draw from the t distribution. 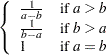
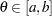
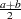

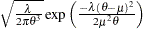
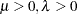
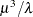
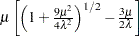
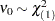 . Let
. Let 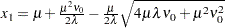 and
and 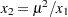 . Perform a Bernoulli trial,
. Perform a Bernoulli trial, 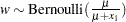 . If
. If 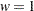 , choose
, choose 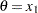 ; otherwise, choose
; otherwise, choose 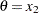
 ,
,  )
) 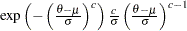
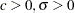
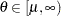 if
if 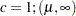 otherwise
otherwise 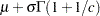
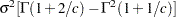
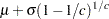 if
if 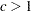
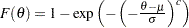 . Generate
. Generate 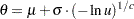 is a draw from the Weibull distribution.
is a draw from the Weibull distribution. 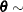 dirich(
dirich( ), where
), where 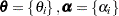 , for
, for 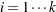
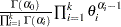 , where
, where 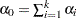
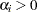
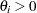 ,
, 
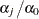
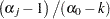
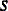 ), both
), both 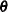 and
and 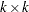 matrics
matrics 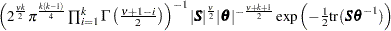
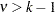
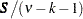
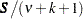
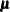 ,
, 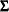 ), where
), where 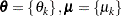 , for
, for  , and
, and 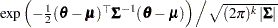
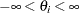
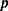 ), where
), where 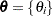 and
and 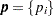 , for
, for 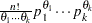 , where
, where 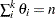
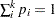 with all
with all 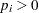
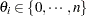 , nonnegative integers
, nonnegative integers 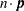
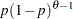 , which counts the total number of trials until the first success.
, which counts the total number of trials until the first success.