The GLIMMIX Procedure

Aspects Common to Adaptive Quadrature and Laplace Approximation

Estimated Precision of Estimates

Denote as 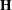$\bH $ the second derivative matrix

\[ \bH = - \frac{\partial ^2 \log \{ L(\bbeta ,\btheta \; \widehat{\bgamma })\} }{\partial [\bbeta ,\btheta ] \partial [\bbeta ',\btheta ']} \]

evaluated at the converged solution of the optimization process. Partition its inverse as

\[ \bH ^{-1} = \left[ \begin{array}{cc} \bC (\bbeta ,\bbeta ) & \bC (\bbeta ,\btheta ) \\ \bC (\btheta ,\bbeta ) & \bC (\btheta ,\btheta ) \end{array} \right] \]

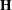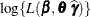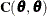For METHOD= LAPLACE and METHOD= QUAD , the GLIMMIX procedure computes $\bH $ by finite forward differences based on the analytic gradient of $\log \{ L(\bbeta ,\btheta \; \widehat{\bgamma })\} $. The partition $\bC (\btheta ,\btheta )$ serves as the asymptotic covariance matrix of the covariance parameter estimates (ASYCOV option in the PROC GLIMMIX statement). The standard errors reported in the "Covariance Parameter Estimates" table are based on the diagonal entries of this partition.

If you request an empirical standard error matrix with the EMPIRICAL option in the PROC GLIMMIX statement, a likelihood-based sandwich estimator is computed based on the subject-specific gradients of the Laplace or quadrature approximation. The sandwich estimator then replaces 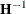$\mb{H}^{-1}$ in calculations following convergence.

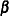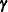To compute the standard errors and prediction standard errors of linear combinations of $\bbeta $ and $\bgamma $, PROC GLIMMIX forms an approximate prediction variance matrix for $[\widehat{\bbeta }, \widehat{\bgamma }]’$ from

\[ \bP = \left[ \begin{array}{cc} \bH ^{-1} & \bH ^{-1} \left( \frac{\partial \widehat{\bgamma }}{\partial [\bbeta ,\btheta ]} \right) \\ \left( \frac{\partial \widehat{\bgamma }}{\partial [\bbeta ',\btheta ']} \right) \bH ^{-1} & \bGamma ^{-1} + \left( \frac{\partial \widehat{\bgamma }}{\partial [\bbeta ',\btheta ']} \right) \bH ^{-1} \left( \frac{\partial \widehat{\bgamma }}{\partial [\bbeta ,\btheta ]} \right) \end{array} \right] \]

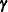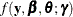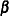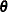where $\bGamma $ is the second derivative matrix from the $\bgamma $ suboptimization that maximizes $f(\mb{y},\bbeta ,\btheta ;\bgamma )$ for given values of $\bbeta $ and $\btheta $. The prediction variance submatrix for the random effects is based on approximating the conditional mean squared error of prediction as in Booth and Hobert (1998). Note that even in the normal linear mixed model, the approximate conditional prediction standard errors are not identical to the prediction standard errors you obtain by inversion of the mixed model equations.

Conditional Fit and Output Statistics

When you estimate the parameters of a mixed model by Laplace approximation or quadrature, the GLIMMIX procedure displays fit statistics related to the marginal distribution as well as the conditional distribution 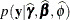$p(\mb{y} | \widehat{\bgamma },\widehat{\bbeta },\widehat{\phi })$. The ODS name of the "Conditional Fit Statistics" table is CondFitStatistics. Because the marginal likelihood is approximated numerically for these methods, statistics based on the marginal distribution are not available. Instead of the generalized Pearson chi-square statistic in the "Fit Statistics" table, PROC GLIMMIX reports the Pearson statistic of the conditional distribution in the "Conditional Fit Statistics" table.

The unavailability of the marginal distribution also affects the set of output statistics that can be produced with METHOD= LAPLACE and METHOD= QUAD . Output statistics and statistical graphics that depend on the marginal variance of the data are not available with these estimation methods.

User-Defined Variance Function

If you provide your own variance function, PROC GLIMMIX generally assumes that the (conditional) distribution of the data is unknown. Laplace or quadrature estimation would then not be possible. When you specify a variance function with METHOD= LAPLACE or METHOD= QUAD , the procedure assumes that the conditional distribution is normal. For example, consider the following statements to fit a mixed model to count data: 

proc glimmix method=laplace;
   class sub;
   _variance_ = _phi_*_mu_;
   model count = x / s link=log;
   random int / sub=sub;
run;

The variance function and the link suggest an overdispersed Poisson model. The Poisson distribution cannot accommodate the extra scale parameter _PHI_, however. In this situation, the GLIMMIX procedure fits a mixed model with random intercepts, log link function, and variance function 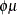$\phi \mu $, assuming that the count variable is normally distributed, given the random effects.

Starting Values

Good starting values for the fixed effects and covariance parameters are important for Laplace and quadrature methods because the process commences with a suboptimization in which the empirical Bayes estimates of the random effects must be obtained before the optimization can get under way. Furthermore, the starting values are important for the adaptive choice of the number of quadrature points.

If you choose METHOD= LAPLACE or METHOD= QUAD and you do not provide starting values for the covariance parameters through the PARMS statement, the GLIMMIX procedure determines starting values in the following steps.

  1. A GLM is fit initially to obtain starting values for the fixed-effects parameters. No output is produced from this stage. The number of initial iterations of this GLM fit can be controlled with the INITITER= option in the PROC GLIMMIX statement. You can suppress this step with the NOINITGLM option in the PROC GLIMMIX statement.

  2. Given the fixed-effects estimates, starting values for the covariance parameters are computed by a MIVQUE0 step (Goodnight 1978a).

  3. For METHOD= QUAD you can follow these steps with several pseudo-likelihood updates to improve on the estimates and to obtain solutions for the random effects. The number of pseudo-likelihood steps is controlled by the INITPL= suboption of METHOD= QUAD .

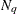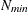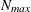  4. For METHOD= QUAD , if you do not specify the number of quadrature points with the suboptions of the METHOD option, the GLIMMIX procedure attempts to determine a sufficient number of points adaptively as follows. Suppose that $N_ q$ denotes the number of nodes in each dimension. 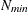If $N_{\mathit{min}}$ and $N_{\mathit{max}}$ denote the values from the QMIN= and QMAX= suboptions, respectively, the sequence for values less than 11 is constructed in increments of 2 starting at $N_{\mathit{min}}$. Values greater than 11 are incremented in steps of r. The default value is r = 10. The default sequence, without specifying the QMIN=, QMAX=, or QFAC= option, is thus 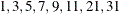$1,3,5,7,9,11,21,31$. If the relative difference of the log-likelihood approximation for two values in the sequence is less than the QTOL=t value (default t = 0.0001), the GLIMMIX procedure uses the lesser value for 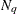$N_ q$ in the subsequent optimization. If the relative difference does not fall below the tolerance t for any two subsequent values in the sequence, no estimation takes place.