The GLIMMIX Procedure
-
Overview

-
Getting Started

-
Syntax
 PROC GLIMMIX StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementCOVTEST StatementEFFECT StatementESTIMATE StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPARMS StatementRANDOM StatementSLICE StatementSTORE StatementWEIGHT StatementProgramming StatementsUser-Defined Link or Variance Function
PROC GLIMMIX StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementCOVTEST StatementEFFECT StatementESTIMATE StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPARMS StatementRANDOM StatementSLICE StatementSTORE StatementWEIGHT StatementProgramming StatementsUser-Defined Link or Variance Function -
Details
 Generalized Linear Models TheoryGeneralized Linear Mixed Models TheoryGLM Mode or GLMM ModeStatistical Inference for Covariance ParametersDegrees of Freedom MethodsEmpirical Covariance ("Sandwich") EstimatorsExploring and Comparing Covariance MatricesProcessing by SubjectsRadial Smoothing Based on Mixed ModelsOdds and Odds Ratio EstimationParameterization of Generalized Linear Mixed ModelsResponse-Level Ordering and ReferencingComparing the GLIMMIX and MIXED ProceduresSingly or Doubly Iterative FittingDefault Estimation TechniquesDefault OutputNotes on Output StatisticsODS Table NamesODS Graphics
Generalized Linear Models TheoryGeneralized Linear Mixed Models TheoryGLM Mode or GLMM ModeStatistical Inference for Covariance ParametersDegrees of Freedom MethodsEmpirical Covariance ("Sandwich") EstimatorsExploring and Comparing Covariance MatricesProcessing by SubjectsRadial Smoothing Based on Mixed ModelsOdds and Odds Ratio EstimationParameterization of Generalized Linear Mixed ModelsResponse-Level Ordering and ReferencingComparing the GLIMMIX and MIXED ProceduresSingly or Doubly Iterative FittingDefault Estimation TechniquesDefault OutputNotes on Output StatisticsODS Table NamesODS Graphics -
Examples
 Binomial Counts in Randomized BlocksMating Experiment with Crossed Random EffectsSmoothing Disease Rates; Standardized Mortality RatiosQuasi-likelihood Estimation for Proportions with Unknown DistributionJoint Modeling of Binary and Count DataRadial Smoothing of Repeated Measures DataIsotonic Contrasts for Ordered AlternativesAdjusted Covariance Matrices of Fixed EffectsTesting Equality of Covariance and Correlation MatricesMultiple Trends Correspond to Multiple Extrema in Profile LikelihoodsMaximum Likelihood in Proportional Odds Model with Random EffectsFitting a Marginal (GEE-Type) ModelResponse Surface Comparisons with Multiplicity AdjustmentsGeneralized Poisson Mixed Model for Overdispersed Count DataComparing Multiple B-SplinesDiallel Experiment with Multimember Random EffectsLinear Inference Based on Summary DataWeighted Multilevel Model for Survey DataQuadrature Method for Multilevel Model
Binomial Counts in Randomized BlocksMating Experiment with Crossed Random EffectsSmoothing Disease Rates; Standardized Mortality RatiosQuasi-likelihood Estimation for Proportions with Unknown DistributionJoint Modeling of Binary and Count DataRadial Smoothing of Repeated Measures DataIsotonic Contrasts for Ordered AlternativesAdjusted Covariance Matrices of Fixed EffectsTesting Equality of Covariance and Correlation MatricesMultiple Trends Correspond to Multiple Extrema in Profile LikelihoodsMaximum Likelihood in Proportional Odds Model with Random EffectsFitting a Marginal (GEE-Type) ModelResponse Surface Comparisons with Multiplicity AdjustmentsGeneralized Poisson Mixed Model for Overdispersed Count DataComparing Multiple B-SplinesDiallel Experiment with Multimember Random EffectsLinear Inference Based on Summary DataWeighted Multilevel Model for Survey DataQuadrature Method for Multilevel Model - References
Example 45.8 Adjusted Covariance Matrices of Fixed Effects
The following data are from Pothoff and Roy (1964) and consist of growth measurements for 11 girls and 16 boys at ages 8, 10, 12, and 14. Some of the observations are suspect (for example, the third observation for person 20); however, all of the data are used here for comparison purposes.
data pr;
input child gender$ y1 y2 y3 y4;
array yy y1-y4;
do time=1 to 4;
age = time*2 + 6;
y = yy{time};
output;
end;
drop y1-y4;
datalines;
1 F 21.0 20.0 21.5 23.0
2 F 21.0 21.5 24.0 25.5
3 F 20.5 24.0 24.5 26.0
4 F 23.5 24.5 25.0 26.5
5 F 21.5 23.0 22.5 23.5
6 F 20.0 21.0 21.0 22.5
7 F 21.5 22.5 23.0 25.0
8 F 23.0 23.0 23.5 24.0
9 F 20.0 21.0 22.0 21.5
10 F 16.5 19.0 19.0 19.5
11 F 24.5 25.0 28.0 28.0
12 M 26.0 25.0 29.0 31.0
13 M 21.5 22.5 23.0 26.5
14 M 23.0 22.5 24.0 27.5
15 M 25.5 27.5 26.5 27.0
16 M 20.0 23.5 22.5 26.0
17 M 24.5 25.5 27.0 28.5
18 M 22.0 22.0 24.5 26.5
19 M 24.0 21.5 24.5 25.5
20 M 23.0 20.5 31.0 26.0
21 M 27.5 28.0 31.0 31.5
22 M 23.0 23.0 23.5 25.0
23 M 21.5 23.5 24.0 28.0
24 M 17.0 24.5 26.0 29.5
25 M 22.5 25.5 25.5 26.0
26 M 23.0 24.5 26.0 30.0
27 M 22.0 21.5 23.5 25.0
;
Jennrich and Schluchter (1986) analyze these data with various models for the fixed effects and the covariance structure. The strategy here is to fit a growth curve model for the boys and girls and to account for subject-to-subject variation through G-side random effects. In addition, serial correlation among the observations within each child is accounted for by a time series process. The data are assumed to be Gaussian, and their –2 restricted log likelihood is minimized to estimate the model parameters.
The following statements fit a mixed model in which a separate growth curve is assumed for each gender:
proc glimmix data=pr; class child gender time; model y = gender age gender*age / covb(details) ddfm=kr; random intercept age / type=chol sub=child; random time / subject=child type=ar(1) residual; ods select ModelInfo CovB CovBModelBased CovBDetails; run;
The growth curve for an individual child differs from the gender-specific trend because of a random intercept and a random slope. The two G-side random effects are assumed to be correlated. Their unstructured covariance matrix is parameterized in terms of the Cholesky root to guarantee a positive (semi-)definite estimate. An AR(1) covariance structure is modeled for the observations over time for each child. Notice the RESIDUAL option in the second RANDOM statement. It identifies this as an R-side random effect.
The DDFM= KR option requests that the covariance matrix of the fixed-effect parameter estimates and denominator degrees of freedom for t and F tests are determined according to Kenward and Roger (1997). This is reflected in the "Model Information" table (Output 45.8.1).
Output 45.8.1: Model Information with DDFM=KR
| Model Information | |
|---|---|
| Data Set | WORK.PR |
| Response Variable | y |
| Response Distribution | Gaussian |
| Link Function | Identity |
| Variance Function | Default |
| Variance Matrix Blocked By | child |
| Estimation Technique | Restricted Maximum Likelihood |
| Degrees of Freedom Method | Kenward-Roger |
| Fixed Effects SE Adjustment | Kenward-Roger |
The COVB option in the MODEL statement requests that the covariance matrix used for inference about fixed effects in this model is displayed; this is the Kenward-Roger-adjusted covariance matrix. The DETAILS suboption requests that the unadjusted covariance matrix is also displayed (Output 45.8.2). In addition, a table of diagnostic measures for the covariance matrices is produced.
Output 45.8.2: Model-Based and Adjusted Covariance Matrix
| Model Based Covariance Matrix for Fixed Effects (Unadjusted) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Effect | gender | Row | Col1 | Col2 | Col3 | Col4 | Col5 | Col6 |
| Intercept | 1 | 0.9969 | -0.9969 | -0.07620 | 0.07620 | |||
| gender | F | 2 | -0.9969 | 2.4470 | 0.07620 | -0.1870 | ||
| gender | M | 3 | ||||||
| age | 4 | -0.07620 | 0.07620 | 0.007581 | -0.00758 | |||
| age*gender | F | 5 | 0.07620 | -0.1870 | -0.00758 | 0.01861 | ||
| age*gender | M | 6 | ||||||
| Diagnostics for Covariance Matrices of Fixed Effects | |||
|---|---|---|---|
| Model-Based | Adjusted | ||
| Dimensions | Rows | 6 | 6 |
| Non-zero entries | 16 | 16 | |
| Summaries | Trace | 3.4701 | 3.3843 |
| Log determinant | -11.95 | -12.17 | |
| Eigenvalues | > 0 | 4 | 4 |
| = 0 | 2 | 2 | |
| max abs | 2.972 | 2.8988 | |
| min abs non-zero | 0.0009 | 0.0008 | |
| Condition number | 3467.8 | 3698.2 | |
| Norms | Frobenius | 3.0124 | 2.9382 |
| Infinity | 3.7072 | 3.6153 | |
| Comparisons | Concordance correlation | 0.9979 | |
| Discrepancy function | 0.0084 | ||
| Frobenius norm of difference | 0.0742 | ||
| Trace(Adjusted Inv(MBased)) | 3.7801 | ||
| Determinant and inversion results apply to the nonsingular partitions of the covariance matrices. | |||
The "Diagnostics for Covariance Matrices" table in Output 45.8.2 consists of several sections. The trace and log determinant of covariance matrices are general scalar summaries that are sometimes used in direct comparisons, or in formulating further statistics, such as the difference of log determinants. The trace simply represents the sum of the variances of all fixed-effects parameters.
The two matrices have the same number of positive and zero eigenvalues; hence they are of the same rank. There are no negative eigenvalues; hence the matrices are positive semi-definite.
The "Comparisons" section of the table provides several statistics that set the matrices in relationship. The statistics enable you to assess the extent to which the adjustment affected the model-based matrix. If the two matrices are identical, the concordance correlation equals 1, the discrepancy function and the Frobenius norm of the differences equal 0, and the trace of the adjusted and the (generalized) inverse of the model-based matrix equals the rank. See the section Exploring and Comparing Covariance Matrices for computational details regarding these statistics. With increasing discrepancy between the matrices, the difference norm and discrepancy function increase, the concordance correlation falls below 1, and the trace deviates from the rank. In this particular example, there is strong agreement between the two matrices; the adjustment to the covariance matrix associated with DDFM= KR is only slight. It is noteworthy, however, that the trace of the adjusted covariance matrix falls short of the trace of the unadjusted one. Indeed, from Output 45.8.2 you can see that the diagonal elements of the adjusted covariance matrices are uniformly smaller than those of the model-based covariance matrix.
Standard error "shrinkage" for the Kenward-Roger covariance adjustment is due to the term 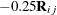 in equation (3) of Kenward and Roger (1997), which is nonzero for covariance structures with second derivatives, such as the TYPE=ANTE(1)
, TYPE=AR(1)
, TYPE=ARH(1)
, TYPE=ARMA(1,1)
, TYPE=CHOL
, TYPE=CSH
, TYPE=FA0(q)
, TYPE=TOEPH
, and TYPE=UNR
structures and all TYPE=SP()
structures.
in equation (3) of Kenward and Roger (1997), which is nonzero for covariance structures with second derivatives, such as the TYPE=ANTE(1)
, TYPE=AR(1)
, TYPE=ARH(1)
, TYPE=ARMA(1,1)
, TYPE=CHOL
, TYPE=CSH
, TYPE=FA0(q)
, TYPE=TOEPH
, and TYPE=UNR
structures and all TYPE=SP()
structures.
For covariance structures that are linear in the parameters, 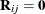 . You can add the FIRSTORDER suboption to the DDFM=
KR option to request that second derivative matrices
. You can add the FIRSTORDER suboption to the DDFM=
KR option to request that second derivative matrices 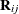 are excluded from computing the covariance matrix adjustment. The resulting covariance adjustment is that of Kackar and Harville
(1984) and Harville and Jeske (1992). This estimator is denoted as
are excluded from computing the covariance matrix adjustment. The resulting covariance adjustment is that of Kackar and Harville
(1984) and Harville and Jeske (1992). This estimator is denoted as 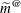 in Harville and Jeske (1992) and is referred to there as the Prasad-Rao estimator after related work by Prasad and Rao (1990). This standard error adjustment is guaranteed to be positive (semi-)definite. The following statements fit the model with
the Kackar-Harville-Jeske estimator and compare model-based and adjusted covariance matrices:
in Harville and Jeske (1992) and is referred to there as the Prasad-Rao estimator after related work by Prasad and Rao (1990). This standard error adjustment is guaranteed to be positive (semi-)definite. The following statements fit the model with
the Kackar-Harville-Jeske estimator and compare model-based and adjusted covariance matrices:
proc glimmix data=pr;
class child gender time;
model y = gender age gender*age / covb(details)
ddfm=kr(firstorder);
random intercept age / type=chol sub=child;
random time / subject=child type=ar(1) residual;
ods select ModelInfo CovB CovBDetails;
run;
The standard error adjustment is reflected in the "Model Information" table (Output 45.8.3).
Output 45.8.3: Model Information with DDFM=KR(FIRSTORDER)
| Model Information | |
|---|---|
| Data Set | WORK.PR |
| Response Variable | y |
| Response Distribution | Gaussian |
| Link Function | Identity |
| Variance Function | Default |
| Variance Matrix Blocked By | child |
| Estimation Technique | Restricted Maximum Likelihood |
| Degrees of Freedom Method | Kenward-Roger |
| Fixed Effects SE Adjustment | Prasad-Rao-Kackar-Harville-Jeske |
Output 45.8.4 displays the adjusted covariance matrix. Notice that the elements of this matrix, in particular the diagonal elements, are larger in absolute value than those of the model-based estimator (Output 45.8.2).
Output 45.8.4: Adjusted Covariance Matrix and Comparison to Model-Based Estimator
| Diagnostics for Covariance Matrices of Fixed Effects | |||
|---|---|---|---|
| Model-Based | Adjusted | ||
| Dimensions | Rows | 6 | 6 |
| Non-zero entries | 16 | 16 | |
| Summaries | Trace | 3.4701 | 3.5234 |
| Log determinant | -11.95 | -11.91 | |
| Eigenvalues | > 0 | 4 | 4 |
| = 0 | 2 | 2 | |
| max abs | 2.972 | 3.0176 | |
| min abs non-zero | 0.0009 | 0.0009 | |
| Condition number | 3467.8 | 3513.4 | |
| Norms | Frobenius | 3.0124 | 3.0587 |
| Infinity | 3.7072 | 3.7647 | |
| Comparisons | Concordance correlation | 0.9999 | |
| Discrepancy function | 0.0003 | ||
| Frobenius norm of difference | 0.0463 | ||
| Trace(Adjusted Inv(MBased)) | 4.0352 | ||
| Determinant and inversion results apply to the nonsingular partitions of the covariance matrices. | |||
The "Comparisons" statistics show that the model-based and adjusted covariance matrix of the fixed-effects parameter estimates are very similar. The concordance correlation is near 1, the discrepancy is near zero, and the trace is very close to the number of positive eigenvalues. This is due to the balanced nature of these repeated measures data. Shrinkage of standard errors, however, can not occur with the Kackar-Harville-Jeske estimator.