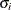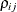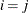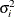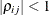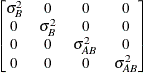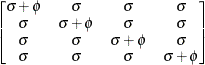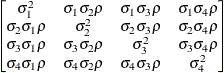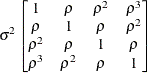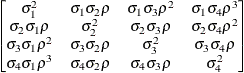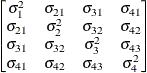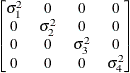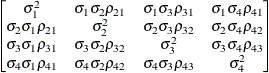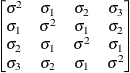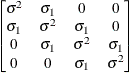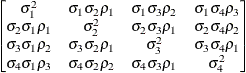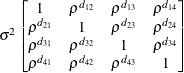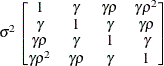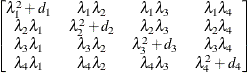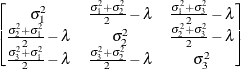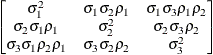-
ANTE(1)
-
specifies a first-order ante-dependence structure
(Kenward 1987; Patel 1991) parameterized in terms of variances and correlation parameters. If t ordered random variables 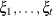 have a first-order ante-dependence structure, then each
have a first-order ante-dependence structure, then each 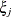 ,
, 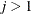 , is independent of all other
, is independent of all other 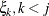 , given
, given 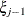 . This Markovian structure is characterized by its inverse variance matrix, which is tridiagonal. Parameterizing an ANTE(1)
structure for a random vector of size t requires 2t – 1 parameters: variances
. This Markovian structure is characterized by its inverse variance matrix, which is tridiagonal. Parameterizing an ANTE(1)
structure for a random vector of size t requires 2t – 1 parameters: variances 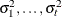 and t – 1 correlation parameters
and t – 1 correlation parameters 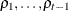 . The covariances among random variables
. The covariances among random variables 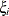 and
and 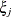 are then constructed as
are then constructed as
PROC GLIMMIX constrains the correlation parameters to satisfy 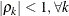 . For variable-order ante-dependence models see Macchiavelli and Arnold (1994).
. For variable-order ante-dependence models see Macchiavelli and Arnold (1994).
-
AR(1)
-
specifies a first-order autoregressive structure,
The values 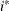 and
and 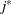 are derived for the ith and jth observations, respectively, and are not necessarily the observation numbers. For example, in the following statements the
values correspond to the class levels for the
are derived for the ith and jth observations, respectively, and are not necessarily the observation numbers. For example, in the following statements the
values correspond to the class levels for the time effect of the ith and jth observation within a particular subject:
proc glimmix;
class time patient;
model y = x x*x;
random time / sub=patient type=ar(1) residual;
run;
PROC GLIMMIX imposes the constraint 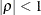 for stationarity.
for stationarity.
-
ARH(1)
-
specifies a heterogeneous first-order autoregressive structure,
with 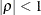 . This covariance structure has the same correlation pattern as the TYPE=AR(1) structure, but the variances are allowed to
differ.
. This covariance structure has the same correlation pattern as the TYPE=AR(1) structure, but the variances are allowed to
differ.
-
ARMA(1,1)
-
specifies the first-order autoregressive moving-average
structure,
Here, 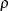 is the autoregressive parameter,
is the autoregressive parameter, 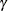 models a moving-average component, and
models a moving-average component, and 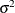 is a scale parameter. In the notation of Fuller (1976, p. 68),
is a scale parameter. In the notation of Fuller (1976, p. 68), 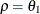 and
and
The example in Table 45.19 and 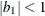 imply that
imply that
where 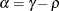 and
and 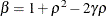 . PROC GLIMMIX imposes the constraints
. PROC GLIMMIX imposes the constraints 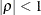 and
and 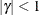 for stationarity, although for some values of
for stationarity, although for some values of 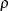 and
and 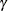 in this region the resulting covariance matrix is not positive definite. When the estimated value of
in this region the resulting covariance matrix is not positive definite. When the estimated value of 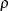 becomes negative, the computed covariance is multiplied by
becomes negative, the computed covariance is multiplied by 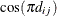 to account for the negativity.
to account for the negativity.
-
CHOL<(q)>
-
specifies an unstructured variance-covariance matrix
parameterized through its Cholesky root. This parameterization ensures that the resulting variance-covariance matrix is at
least positive semidefinite. If all diagonal values are nonzero, it is positive definite. For example, a 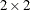 unstructured covariance matrix can be written as
unstructured covariance matrix can be written as
Without imposing constraints on the three parameters, there is no guarantee that the estimated variance matrix is positive
definite. Even if 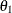 and
and 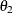 are nonzero, a large value for
are nonzero, a large value for 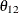 can lead to a negative eigenvalue of
can lead to a negative eigenvalue of ![$\mr{Var}[\bxi ]$](images/statug_glimmix0357.png) . The Cholesky root of a positive definite matrix
. The Cholesky root of a positive definite matrix 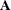 is a lower triangular matrix
is a lower triangular matrix 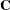 such that
such that 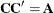 . The Cholesky root of the above
. The Cholesky root of the above 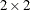 matrix can be written as
matrix can be written as
The elements of the unstructured variance matrix are then simply 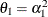 ,
, 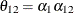 , and
, and 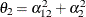 . Similar operations yield the generalization to covariance matrices of higher orders.
. Similar operations yield the generalization to covariance matrices of higher orders.
For example, the following statements model the covariance matrix of each subject as an unstructured matrix:
proc glimmix;
class sub;
model y = x;
random _residual_ / subject=sub type=un;
run;
The next set of statements accomplishes the same, but the estimated  matrix is guaranteed to be nonnegative definite:
matrix is guaranteed to be nonnegative definite:
proc glimmix;
class sub;
model y = x;
random _residual_ / subject=sub type=chol;
run;
The GLIMMIX procedure constrains the diagonal elements of the Cholesky root to be positive. This guarantees a unique solution
when the matrix is positive definite.
The optional order parameter 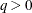 determines how many bands below the diagonal are modeled. Elements in the lower triangular portion of
determines how many bands below the diagonal are modeled. Elements in the lower triangular portion of 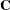 in bands higher than q are set to zero. If you consider the resulting covariance matrix
in bands higher than q are set to zero. If you consider the resulting covariance matrix 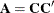 , then the order parameter has the effect of zeroing all off-diagonal elements that are at least q positions away from the diagonal.
, then the order parameter has the effect of zeroing all off-diagonal elements that are at least q positions away from the diagonal.
Because of its good computational and statistical properties, the Cholesky root parameterization is generally recommended
over a completely unstructured covariance matrix (TYPE=UN
). However, it is computationally slightly more involved.
-
CS
-
specifies the compound-symmetry structure, which
has constant variance and constant covariance
The compound symmetry structure arises naturally with nested random effects, such as when subsampling error is nested within
experimental error. The models constructed with the following two sets of GLIMMIX statements have the same marginal variance
matrix, provided  is positive:
is positive:
proc glimmix;
class block A;
model y = block A;
random block*A / type=vc;
run;
proc glimmix;
class block A;
model y = block A;
random _residual_ / subject=block*A
type=cs;
run;
In the first case, the block*A random effect models the G-side experimental error. Because the distribution defaults to the normal, the 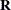 matrix is of form
matrix is of form 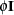 (see Table 45.20), and
(see Table 45.20), and  is the subsampling error variance. The marginal variance for the data from a particular experimental unit is thus
is the subsampling error variance. The marginal variance for the data from a particular experimental unit is thus 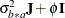 . This matrix is of compound symmetric form.
. This matrix is of compound symmetric form.
Hierarchical random assignments or selections, such as subsampling or split-plot designs, give rise to compound symmetric
covariance structures. This implies exchangeability of the observations on the subunit, leading to constant correlations between
the observations. Compound symmetric structures are thus usually not appropriate for processes where correlations decline
according to some metric, such as spatial and temporal processes.
Note that R-side compound-symmetry structures do not impose any constraint on  . You can thus use an R-side TYPE=CS structure to emulate a variance-component model with unbounded estimate of the variance
component.
. You can thus use an R-side TYPE=CS structure to emulate a variance-component model with unbounded estimate of the variance
component.
-
CSH
-
specifies the heterogeneous compound-symmetry structure, which is an
equi-correlation structure but allows for different variances
-
FA(q)
-
specifies the factor-analytic structure with q factors
(Jennrich and Schluchter 1986). This structure is of the form 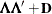 , where
, where 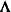 is a
is a 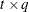 rectangular matrix and
rectangular matrix and 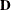 is a
is a 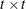 diagonal matrix with t different parameters. When
diagonal matrix with t different parameters. When 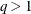 , the elements of
, the elements of 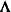 in its upper-right corner (that is, the elements in the ith row and jth column for
in its upper-right corner (that is, the elements in the ith row and jth column for 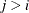 ) are set to zero to fix the rotation of the structure.
) are set to zero to fix the rotation of the structure.
-
FA0(q)
-
specifies a factor-analytic structure with q factors of the
form ![$\mr{Var}[\bxi ] = \bLambda \bLambda ’$](images/statug_glimmix0377.png) , where
, where 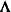 is a
is a 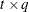 rectangular matrix and t is the dimension of
rectangular matrix and t is the dimension of 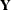 . When
. When 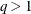 ,
, 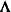 is a lower triangular matrix. When
is a lower triangular matrix. When 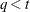 —that is, when the number of factors is less than the dimension of the matrix—this structure is nonnegative definite but not
of full rank. In this situation, you can use it to approximate an unstructured covariance matrix.
—that is, when the number of factors is less than the dimension of the matrix—this structure is nonnegative definite but not
of full rank. In this situation, you can use it to approximate an unstructured covariance matrix.
-
HF
-
specifies a covariance structure that satisfies the general
Huynh-Feldt condition (Huynh and Feldt 1970). For a random vector with t elements, this structure has 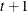 positive parameters and covariances
positive parameters and covariances
A covariance matrix 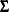 generally satisfies the Huynh-Feldt condition if it can be written as
generally satisfies the Huynh-Feldt condition if it can be written as 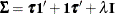 . The preceding parameterization chooses
. The preceding parameterization chooses 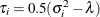 . Several simpler covariance structures give rise to covariance matrices that also satisfy the Huynh-Feldt condition. For
example, TYPE=CS
, TYPE=VC
, and TYPE=UN(1)
are nested within TYPE=HF. You can use the COVTEST
statement to test the HF structure against one of these simpler structures. Note also that the HF structure is nested within
an unstructured covariance matrix.
. Several simpler covariance structures give rise to covariance matrices that also satisfy the Huynh-Feldt condition. For
example, TYPE=CS
, TYPE=VC
, and TYPE=UN(1)
are nested within TYPE=HF. You can use the COVTEST
statement to test the HF structure against one of these simpler structures. Note also that the HF structure is nested within
an unstructured covariance matrix.
The TYPE=HF covariance structure can be sensitive to the choice of starting values and the default MIVQUE(0) starting values
can be poor for this structure; you can supply your own starting values with the PARMS
statement.
-
LIN(q)
-
specifies a general linear covariance structure with q parameters.
This structure consists of a linear combination of known matrices that you input with the LDATA=
option. Suppose that you want to model the covariance of a random vector of length t, and further suppose that 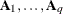 are symmetric
are symmetric 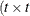 ) matrices constructed from the information in the LDATA=
data set. Then,
) matrices constructed from the information in the LDATA=
data set. Then,
where ![$[\bA _ k]_{ij}$](images/statug_glimmix0386.png) denotes the element in row i, column j of matrix
denotes the element in row i, column j of matrix 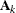 .
.
Linear structures are very flexible and general. You need to exercise caution to ensure that the variance matrix is positive
definite. Note that PROC GLIMMIX does not impose boundary constraints on the parameters 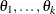 of a general linear covariance structure. For example, if classification variable
of a general linear covariance structure. For example, if classification variable A has 6 levels, the following statements fit a variance component structure for the random effect without boundary constraints:
data ldata;
retain parm 1 value 1;
do row=1 to 6; col=row; output; end;
run;
proc glimmix data=MyData;
class A B;
model Y = B;
random A / type=lin(1) ldata=ldata;
run;
-
PSPLINE<(options)>
-
requests that PROC GLIMMIX form a B-spline basis and fits a
penalized B-spline (P-spline, Eilers and Marx 1996) with random spline coefficients. This covariance structure is available only for G-side random effects and only a single
continuous random effect can be specified with TYPE=PSPLINE. As for TYPE=RSMOOTH, PROC GLIMMIX forms a modified 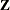 matrix and fits a mixed model in which the random variables associated with the columns of
matrix and fits a mixed model in which the random variables associated with the columns of 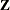 are independent with a common variance. The
are independent with a common variance. The 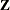 matrix is constructed as follows.
matrix is constructed as follows.
Denote as 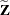 the
the 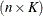 matrix of B-splines of degree d and denote as
matrix of B-splines of degree d and denote as 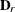 the
the 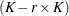 matrix of rth-order differences. For example, for K = 5,
matrix of rth-order differences. For example, for K = 5,
Then, the 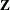 matrix used in fitting the mixed model is the
matrix used in fitting the mixed model is the 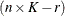 matrix
matrix
The construction of the B-spline knots is controlled with the KNOTMETHOD=
EQUAL(m) option and the DEGREE=d suboption of TYPE=PSPLINE. The total number of knots equals the number m of equally spaced interior knots plus d knots at the low end and 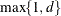 knots at the high end. The number of columns in the B-spline basis equals K = m + d + 1. By default, the interior knots exclude the minimum and maximum of the random-effect values and are based on m – 1 equally spaced intervals. Suppose
knots at the high end. The number of columns in the B-spline basis equals K = m + d + 1. By default, the interior knots exclude the minimum and maximum of the random-effect values and are based on m – 1 equally spaced intervals. Suppose 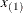 and
and 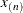 are the smallest and largest random-effect values; then interior knots are placed at
are the smallest and largest random-effect values; then interior knots are placed at
In addition, d evenly spaced exterior knots are placed below 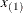 and
and 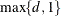 exterior knots are placed above
exterior knots are placed above 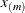 . The exterior knots are evenly spaced and start at
. The exterior knots are evenly spaced and start at 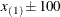 times the machine epsilon. For example, based on the defaults d = 3, r = 3, the following statements lead to 26 total knots and 21 columns in
times the machine epsilon. For example, based on the defaults d = 3, r = 3, the following statements lead to 26 total knots and 21 columns in 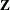 , m = 20, K = m + d + 1 = 24, K – r = 21:
, m = 20, K = m + d + 1 = 24, K – r = 21:
proc glimmix;
model y = x;
random x / type=pspline knotmethod=equal(20);
run;
Details about the computation and properties of B-splines can be found in De Boor (2001). You can extend or limit the range of the knots with the KNOTMIN=
and KNOTMAX=
options. Table 45.18 lists some of the parameters that control this covariance type and their relationships.
Table 45.18: P-Spline Parameters
|
Parameter
|
Description
|
|
d
|
Degree of B-spline, default d = 3
|
|
r
|
Order of differencing in construction of 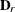 , default r = 3 , default r = 3
|
|
m
|
Number of interior knots, default 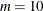
|
|
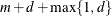
|
Total number of knots
|
|
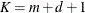
|
Number of columns in B-spline basis
|
|
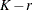
|
Number of columns in 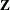
|
You can specify the following options for TYPE=PSPLINE:
- DEGREE=d
-
specifies the degree of the B-spline. The default is d = 3.
- DIFFORDER=r
-
specifies the order of the differencing matrix 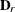 . The default and maximum is r = 3.
. The default and maximum is r = 3.
-
RSMOOTH<(m | NOLOG)>
-
specifies a radial smoother covariance structure for G-side random
effects. This results in an approximate low-rank thin-plate spline where the smoothing parameter is obtained by the estimation
method selected with the METHOD=
option of the PROC GLIMMIX
statement. The smoother is based on the automatic smoother in Ruppert, Wand, and Carroll (2003, Chapter 13.4–13.5), but with a different method of selecting the spline knots. See the section Radial Smoothing Based on Mixed Models for further details about the construction of the smoother and the knot selection.
Radial smoothing is possible in one or more dimensions. A univariate smoother is obtained with a single random effect, while
multiple random effects in a RANDOM statement yield a multivariate smoother. Only continuous random effects are permitted
with this covariance structure. If 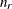 denotes the number of continuous random effects in the RANDOM statement, then the covariance structure of the random effects
denotes the number of continuous random effects in the RANDOM statement, then the covariance structure of the random effects
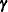 is determined as follows. Suppose that
is determined as follows. Suppose that 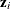 denotes the vector of random effects for the ith observation. Let
denotes the vector of random effects for the ith observation. Let 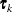 denote the
denote the 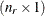 vector of knot coordinates,
vector of knot coordinates, 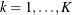 , and K is the total number of knots. The Euclidean distance between the knots is computed as
, and K is the total number of knots. The Euclidean distance between the knots is computed as
and the distance between knots and effects is computed as
The 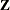 matrix for the GLMM is constructed as
matrix for the GLMM is constructed as
where the 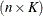 matrix
matrix 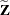 has typical element
has typical element
and the 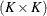 matrix
matrix 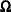 has typical element
has typical element
The exponent in these expressions equals 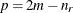 , where the optional value m corresponds to the derivative penalized in the thin-plate spline. A larger value of m will yield a smoother fit. The GLIMMIX procedure requires p > 0 and chooses by default m = 2 if
, where the optional value m corresponds to the derivative penalized in the thin-plate spline. A larger value of m will yield a smoother fit. The GLIMMIX procedure requires p > 0 and chooses by default m = 2 if 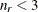 and
and 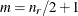 otherwise. The NOLOG option removes the
otherwise. The NOLOG option removes the 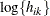 and
and 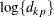 terms from the computation of the
terms from the computation of the 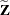 and
and 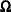 matrices when
matrices when 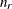 is even; this yields invariance under rescaling of the coordinates.
is even; this yields invariance under rescaling of the coordinates.
Finally, the components of 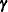 are assumed to have equal variance
are assumed to have equal variance 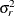 . The "smoothing parameter"
. The "smoothing parameter" 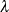 of the low-rank spline is related to the variance components in the model,
of the low-rank spline is related to the variance components in the model, 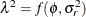 . See Ruppert, Wand, and Carroll (2003) for details. If the conditional distribution does not provide a scale parameter
. See Ruppert, Wand, and Carroll (2003) for details. If the conditional distribution does not provide a scale parameter  , you can add a single R-side residual parameter.
, you can add a single R-side residual parameter.
The knot selection is controlled with the KNOTMETHOD=
option. The GLIMMIX procedure selects knots automatically based on the vertices of a k-d tree or reads knots from a data set that you supply. See the section Radial Smoothing Based on Mixed Models for further details on radial smoothing in the GLIMMIX procedure and its connection to a mixed model formulation.
-
SIMPLE
-
is an alias for TYPE=VC.
-
SP(EXP)(c-list)
-
models an exponential spatial or temporal covariance structure,
where the covariance between two observations depends on a distance metric 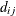 . The c-list contains the names of the numeric variables used as coordinates to determine distance. For a stochastic process in
. The c-list contains the names of the numeric variables used as coordinates to determine distance. For a stochastic process in 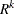 , there are k elements in c-list. If the
, there are k elements in c-list. If the 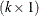 vectors of coordinates for observations i and j are
vectors of coordinates for observations i and j are 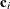 and
and 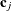 , then PROC GLIMMIX computes the Euclidean distance
, then PROC GLIMMIX computes the Euclidean distance
The covariance between two observations is then
The parameter  is not what is commonly referred to as the range parameter in geostatistical applications. The practical range of a (second-order
stationary) spatial process is the distance
is not what is commonly referred to as the range parameter in geostatistical applications. The practical range of a (second-order
stationary) spatial process is the distance 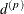 at which the correlations fall below 0.05. For the SP(EXP) structure, this distance is
at which the correlations fall below 0.05. For the SP(EXP) structure, this distance is 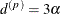 . PROC GLIMMIX constrains
. PROC GLIMMIX constrains  to be positive.
to be positive.
-
SP(GAU)(c-list)
-
models a Gaussian covariance structure,
See TYPE=SP(EXP) for the computation of the distance 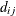 . The parameter
. The parameter  is related to the range of the process as follows. If the practical range
is related to the range of the process as follows. If the practical range 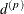 is defined as the distance at which the correlations fall below 0.05, then
is defined as the distance at which the correlations fall below 0.05, then 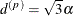 . PROC GLIMMIX constrains
. PROC GLIMMIX constrains  to be positive. See TYPE=SP(EXP) for the computation of the distance
to be positive. See TYPE=SP(EXP) for the computation of the distance 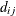 from the variables specified in c-list.
from the variables specified in c-list.
-
SP(MAT)(c-list)
-
models a covariance structure in the Matérn class of covariance
functions (Matérn 1986). The covariance is expressed in the parameterization of Handcock and Stein (1993); Handcock and Wallis (1994); it can be written as
The function 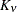 is the modified Bessel function of the second kind of (real) order
is the modified Bessel function of the second kind of (real) order 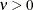 . The smoothness (continuity) of a stochastic process with covariance function in the Matérn class increases with
. The smoothness (continuity) of a stochastic process with covariance function in the Matérn class increases with  . This class thus enables data-driven estimation of the smoothness properties of the process. The covariance is identical
to the exponential model for
. This class thus enables data-driven estimation of the smoothness properties of the process. The covariance is identical
to the exponential model for 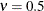 (TYPE=SP(EXP)(c-list)), while for
(TYPE=SP(EXP)(c-list)), while for 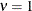 the model advocated by Whittle (1954) results. As
the model advocated by Whittle (1954) results. As 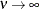 , the model approaches the Gaussian covariance structure (TYPE=SP(GAU)(c-list)).
, the model approaches the Gaussian covariance structure (TYPE=SP(GAU)(c-list)).
Note that the MIXED procedure offers covariance structures in the Matérn class in two parameterizations, TYPE=SP(MATERN) and
TYPE=SP(MATHSW). The TYPE=SP(MAT) in the GLIMMIX procedure is equivalent to TYPE=SP(MATHSW) in the MIXED procedure.
Computation of the function 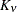 and its derivatives is numerically demanding; fitting models with Matérn covariance structures can be time-consuming. Good
starting values are essential.
and its derivatives is numerically demanding; fitting models with Matérn covariance structures can be time-consuming. Good
starting values are essential.
-
SP(POW)(c-list)
-
models a power covariance structure,
where 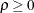 . This is a reparameterization of the exponential structure, TYPE=SP(EXP). Specifically,
. This is a reparameterization of the exponential structure, TYPE=SP(EXP). Specifically, 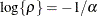 . See TYPE=SP(EXP) for the computation of the distance
. See TYPE=SP(EXP) for the computation of the distance 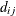 from the variables specified in c-list. When the estimated value of
from the variables specified in c-list. When the estimated value of 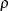 becomes negative, the computed covariance is multiplied by
becomes negative, the computed covariance is multiplied by 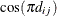 to account for the negativity.
to account for the negativity.
-
SP(POWA)(c-list)
-
models an anisotropic power covariance structure in k dimensions,
provided that the coordinate list c-list has k elements. If 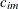 denotes the coordinate for the ith observation of the mth variable in c-list, the covariance between two observations is given by
denotes the coordinate for the ith observation of the mth variable in c-list, the covariance between two observations is given by
Note that for k = 1, TYPE=SP(POWA) is equivalent to TYPE=SP(POW), which is itself a reparameterization of TYPE=SP(EXP). When the estimated
value of 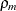 becomes negative, the computed covariance is multiplied by
becomes negative, the computed covariance is multiplied by 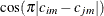 to account for the negativity.
to account for the negativity.
-
SP(SPH)(c-list)
-
models a spherical covariance structure,
The spherical covariance structure has a true range parameter. The covariances between observations are exactly zero when
their distance exceeds  . See TYPE=SP(EXP) for the computation of the distance
. See TYPE=SP(EXP) for the computation of the distance 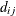 from the variables specified in c-list.
from the variables specified in c-list.
-
TOEP
-
models a Toeplitz covariance structure. This structure can be viewed
as an autoregressive structure with order equal to the dimension of the matrix,
-
TOEP(q)
-
specifies a banded Toeplitz structure,
This can be viewed as a moving-average structure with order equal to q – 1. The specification TYPE=TOEP(1) is the same as 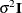 , and it can be useful for specifying the same variance component for several effects.
, and it can be useful for specifying the same variance component for several effects.
-
TOEPH<(q)>
-
models a Toeplitz covariance structure. The correlations of this
structure are banded as the TOEP or TOEP(q) structures, but the variances are allowed to vary:
The correlation parameters satisfy 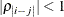 . If you specify the optional value q, the correlation parameters with
. If you specify the optional value q, the correlation parameters with 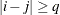 are set to zero, creating a banded correlation structure. The specification TYPE=TOEPH(1) results in a diagonal covariance
matrix with heterogeneous variances.
are set to zero, creating a banded correlation structure. The specification TYPE=TOEPH(1) results in a diagonal covariance
matrix with heterogeneous variances.
-
UN<(q)>
-
specifies a completely general (unstructured) covariance matrix
parameterized directly in terms of variances and covariances,
The variances are constrained to be nonnegative, and the covariances are unconstrained. This structure is not constrained
to be nonnegative definite in order to avoid nonlinear constraints; however, you can use the TYPE=CHOL structure if you want
this constraint to be imposed by a Cholesky factorization. If you specify the order parameter q, then PROC GLIMMIX estimates only the first q bands of the matrix, setting elements in all higher bands equal to 0.
-
UNR<(q)>
-
specifies a completely general (unstructured) covariance matrix
parameterized in terms of variances and correlations,
where 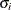 denotes the standard deviation and the correlation
denotes the standard deviation and the correlation 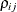 is zero when
is zero when 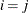 and when
and when 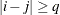 , provided the order parameter q is given. This structure fits the same model as the TYPE=UN(q) option, but with a different parameterization. The ith variance parameter is
, provided the order parameter q is given. This structure fits the same model as the TYPE=UN(q) option, but with a different parameterization. The ith variance parameter is 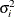 . The parameter
. The parameter 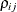 is the correlation between the ith and jth measurements; it satisfies
is the correlation between the ith and jth measurements; it satisfies 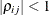 . If you specify the order parameter q, then PROC GLIMMIX estimates only the first q bands of the matrix, setting all higher bands equal to zero.
. If you specify the order parameter q, then PROC GLIMMIX estimates only the first q bands of the matrix, setting all higher bands equal to zero.
-
VC
-
specifies standard variance components and is the default structure
for both G-side and R-side covariance structures. In a G-side covariance structure, a distinct variance component is assigned
to each effect. In an R-side structure TYPE=VC is usually used only to add overdispersion effects or with the GROUP=
option to specify a heterogeneous variance model.


 PROC GLIMMIX StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementCOVTEST StatementEFFECT StatementESTIMATE StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPARMS StatementRANDOM StatementSLICE StatementSTORE StatementWEIGHT StatementProgramming StatementsUser-Defined Link or Variance Function
PROC GLIMMIX StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementCOVTEST StatementEFFECT StatementESTIMATE StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPARMS StatementRANDOM StatementSLICE StatementSTORE StatementWEIGHT StatementProgramming StatementsUser-Defined Link or Variance Function Generalized Linear Models TheoryGeneralized Linear Mixed Models TheoryGLM Mode or GLMM ModeStatistical Inference for Covariance ParametersDegrees of Freedom MethodsEmpirical Covariance ("Sandwich") EstimatorsExploring and Comparing Covariance MatricesProcessing by SubjectsRadial Smoothing Based on Mixed ModelsOdds and Odds Ratio EstimationParameterization of Generalized Linear Mixed ModelsResponse-Level Ordering and ReferencingComparing the GLIMMIX and MIXED ProceduresSingly or Doubly Iterative FittingDefault Estimation TechniquesDefault OutputNotes on Output StatisticsODS Table NamesODS Graphics
Generalized Linear Models TheoryGeneralized Linear Mixed Models TheoryGLM Mode or GLMM ModeStatistical Inference for Covariance ParametersDegrees of Freedom MethodsEmpirical Covariance ("Sandwich") EstimatorsExploring and Comparing Covariance MatricesProcessing by SubjectsRadial Smoothing Based on Mixed ModelsOdds and Odds Ratio EstimationParameterization of Generalized Linear Mixed ModelsResponse-Level Ordering and ReferencingComparing the GLIMMIX and MIXED ProceduresSingly or Doubly Iterative FittingDefault Estimation TechniquesDefault OutputNotes on Output StatisticsODS Table NamesODS Graphics Binomial Counts in Randomized BlocksMating Experiment with Crossed Random EffectsSmoothing Disease Rates; Standardized Mortality RatiosQuasi-likelihood Estimation for Proportions with Unknown DistributionJoint Modeling of Binary and Count DataRadial Smoothing of Repeated Measures DataIsotonic Contrasts for Ordered AlternativesAdjusted Covariance Matrices of Fixed EffectsTesting Equality of Covariance and Correlation MatricesMultiple Trends Correspond to Multiple Extrema in Profile LikelihoodsMaximum Likelihood in Proportional Odds Model with Random EffectsFitting a Marginal (GEE-Type) ModelResponse Surface Comparisons with Multiplicity AdjustmentsGeneralized Poisson Mixed Model for Overdispersed Count DataComparing Multiple B-SplinesDiallel Experiment with Multimember Random EffectsLinear Inference Based on Summary DataWeighted Multilevel Model for Survey DataQuadrature Method for Multilevel Model
Binomial Counts in Randomized BlocksMating Experiment with Crossed Random EffectsSmoothing Disease Rates; Standardized Mortality RatiosQuasi-likelihood Estimation for Proportions with Unknown DistributionJoint Modeling of Binary and Count DataRadial Smoothing of Repeated Measures DataIsotonic Contrasts for Ordered AlternativesAdjusted Covariance Matrices of Fixed EffectsTesting Equality of Covariance and Correlation MatricesMultiple Trends Correspond to Multiple Extrema in Profile LikelihoodsMaximum Likelihood in Proportional Odds Model with Random EffectsFitting a Marginal (GEE-Type) ModelResponse Surface Comparisons with Multiplicity AdjustmentsGeneralized Poisson Mixed Model for Overdispersed Count DataComparing Multiple B-SplinesDiallel Experiment with Multimember Random EffectsLinear Inference Based on Summary DataWeighted Multilevel Model for Survey DataQuadrature Method for Multilevel Model matrix of the mixed model, the random effects in the
matrix of the mixed model, the random effects in the  vector, the structure of
vector, the structure of 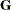 , and the structure of
, and the structure of 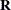 .
.
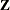 matrix is constructed exactly like the
matrix is constructed exactly like the 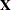 matrix for the fixed effects, and the
matrix for the fixed effects, and the 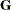 matrix is constructed to correspond to the effects constituting
matrix is constructed to correspond to the effects constituting 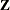 . The structures of
. The structures of 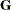 and
and 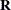 are defined by using the TYPE=
option described on . The random effects can be classification or continuous effects, and multiple RANDOM statements are
possible.
are defined by using the TYPE=
option described on . The random effects can be classification or continuous effects, and multiple RANDOM statements are
possible.
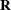 matrix. Basically, the _RESIDUAL_ keyword takes the place of the random-effect if you want to specify
R-side variances and covariance structures. These keywords take precedence over variables in the data set with the same name. If your data or the covariance structure requires that
an effect is specified, you can use the RESIDUAL
option to instruct the GLIMMIX procedure to model the R-side variances and covariances.
matrix. Basically, the _RESIDUAL_ keyword takes the place of the random-effect if you want to specify
R-side variances and covariance structures. These keywords take precedence over variables in the data set with the same name. If your data or the covariance structure requires that
an effect is specified, you can use the RESIDUAL
option to instruct the GLIMMIX procedure to model the R-side variances and covariances.
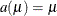 is replaced by
is replaced by 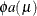 :
:

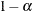
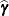
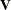
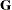
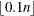
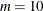
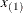
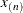
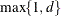
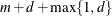
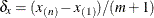
![\[ x_{(1)} + j\delta _ x, \quad j=1,\ldots ,m \]](images/statug_glimmix0311.png)
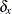
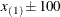
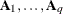
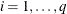
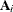
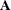
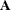
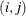
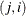
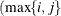
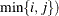
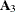
![\[ \left[ \begin{array}{llll} 0 & & & \\ 5 & 0 & & \\ 0 & 0 & 0 & \\ 0 & 0 & 0 & 0 \end{array} \right] \]](images/statug_glimmix0323.png)
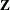
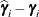
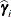
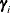
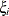
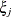
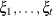
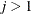
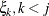
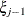
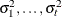
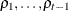
![\[ \mr{Cov}\left[\xi _ i,\xi _ j\right] = \sqrt {\sigma ^2_ i\sigma ^2_ j} \, \prod _{k=i}^{j-1}\rho _ k \]](images/statug_glimmix0335.png)
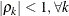
![\[ \mr{Cov}\left[\xi _ i,\xi _ j\right] = \sigma ^2 \rho ^{|i^* - j^*|} \]](images/statug_glimmix0337.png)
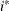
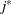
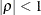
![\[ \mr{Cov}\left[\xi _ i,\xi _ j\right] = \sqrt {\sigma ^2_ i \sigma ^2_ j} \, \rho ^{|i^* - j^*|} \]](images/statug_glimmix0341.png)
![\[ \mr{Cov}\left[\xi _ i,\xi _ j\right] = \left\{ \begin{array}{ll} \sigma ^2 & i=j \\ \sigma ^2 \gamma \rho ^{|i^*-j^*|-1} & i \not= j \end{array} \right. \]](images/statug_glimmix0342.png)
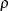
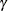
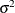
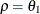
![\[ \gamma = \frac{(1 + b_1\theta _1)(\theta _1 + b_1)}{1 + b^2_1 + 2 b_1 \theta _1} \]](images/statug_glimmix0346.png)
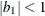
![\[ b_1 = \frac{\beta - \sqrt {\beta ^2 - 4\alpha ^2}}{2\alpha } \]](images/statug_glimmix0348.png)
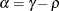
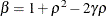
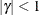
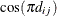
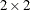
![\[ \mr{Var}[\bxi ] = \left[ \begin{array}{cc} \theta _1 & \theta _{12} \\ \theta _{12} & \theta _2 \end{array} \right] \]](images/statug_glimmix0353.png)
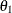
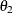
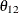
![$\mr{Var}[\bxi ]$](images/statug_glimmix0357.png)
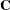
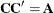
![\[ \mb{C} = \left[ \begin{array}{cc} \alpha _1 & 0 \\ \alpha _{12} & \alpha _2 \end{array} \right] \]](images/statug_glimmix0359.png)
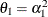
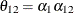
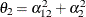
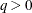
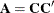
![\[ \mr{Cov}\left[\xi _ i,\xi _ j\right] = \left\{ \begin{array}{lc} \phi + \sigma & i=j \\ \sigma & i \not= j \end{array} \right. \]](images/statug_glimmix0365.png)

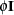

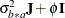
![\[ \mr{Cov}\left[\xi _ i,\xi _ j\right] = \left\{ \begin{array}{lc} \sqrt {\sigma ^2_ i\sigma ^2_ j} & i=j \\ \rho \sqrt {\sigma ^2_ i\sigma ^2_ j} & i \not= j \end{array} \right. \]](images/statug_glimmix0369.png)
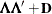
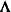
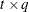
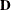
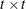
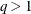
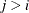
![$\mr{Var}[\bxi ] = \bLambda \bLambda ’$](images/statug_glimmix0377.png)
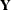
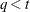
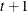
![\[ \mr{Cov}\left[\xi _ i,\xi _ j\right] = \left\{ \begin{array}{ll} \sigma ^2_ i & i = j \\ 0.5(\sigma ^2_ i+\sigma ^2_ j) - \lambda & i \not= j \end{array} \right. \]](images/statug_glimmix0381.png)
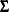
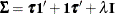
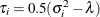
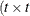
![\[ \mr{Cov}\left[\xi _ i,\xi _ j\right] = \sum _{k=1}^{q} \theta _ k [\bA _ k]_{ij} \]](images/statug_glimmix0385.png)
![$[\bA _ k]_{ij}$](images/statug_glimmix0386.png)
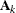
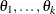
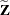
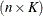
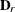
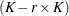
![\begin{align*} \mb{D}_1 & = \left[ \begin{array}{rrrrr} 1 & -1 & 0 & 0 & 0 \\ 0 & 1 & -1 & 0 & 0 \\ 0 & 0 & 1 & -1 & 0 \\ 0 & 0 & 0 & 1 & -1 \end{array} \right] \\ \mb{D}_2 & = \left[ \begin{array}{rrrrr} 1 & -2 & 1 & 0 & 0 \\ 0 & 1 & -2 & 1 & 0 \\ 0 & 0 & 1 & -2 & 1 \end{array}\right] \\ \mb{D}_3 & = \left[ \begin{array}{rrrrr} 1 & -3 & 3 & -1 & 0 \\ 0 & 1 & -3 & 3 & -1 \end{array} \right] \end{align*}](images/statug_glimmix0393.png)
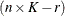
![\[ \mb{Z} = \widetilde{\mb{Z}}(\mb{D}_ r’\mb{D}_ r)^-\mb{D}_ r’ \]](images/statug_glimmix0395.png)
![\[ x_{(1)} + j(x_{(n)} - x_{(1)})/(m+1), \quad j=1,\ldots ,m \]](images/statug_glimmix0397.png)
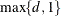
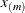
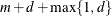
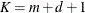
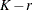
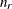
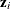
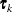
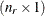
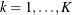
![\[ d_{kp} = ||\btau _ k - \btau _ p|| = \sqrt {\sum _{j=1}^{n_ r} (\tau _{jk}-\tau _{jp})^2} \]](images/statug_glimmix0408.png)
![\[ h_{ik} = ||\mb{z}_ i - \btau _ k|| = \sqrt {\sum _{j=1}^{n_ r} (z_{ij}-\tau _{jk})^2} \]](images/statug_glimmix0409.png)
![\[ \bZ = \widetilde{\bZ }\bOmega ^{-1/2} \]](images/statug_glimmix0410.png)
![\[ [\widetilde{\bZ }]_{ik} = \left\{ \begin{array}{ll} h_{ik}^ p & n_ r \, \, \mr{odd} \\ h_{ik}^ p \, \log \{ h_{ik}\} & n_ r \, \, \mr{even} \end{array} \right. \]](images/statug_glimmix0411.png)
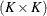
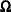
![\[ [\bOmega ]_{kp} = \left\{ \begin{array}{ll} d_{kp}^ p & n_ r \, \, \mr{odd} \\ d_{kp}^ p \log \{ d_{kp}\} & n_ r \, \, \mr{even} \end{array} \right. \]](images/statug_glimmix0414.png)
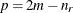
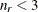
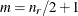
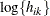
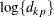
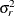
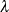
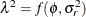
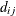
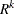
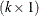
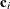
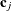
![\[ d_{ij} = ||\mb{c}_ i - \mb{c}_ j|| = \sqrt {\sum _{m=1}^{k}(c_{mi} - c_{mj})^2} \]](images/statug_glimmix0426.png)
![\[ \mr{Cov}\left[\xi _ i,\xi _ j\right] = \sigma ^2 \exp \{ -d_{ij} / \alpha \} \]](images/statug_glimmix0427.png)
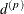
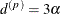
![\[ \mr{Cov}\left[\xi _ i,\xi _ j\right] = \sigma ^2 \exp \{ -d_{ij}^2 / \alpha ^2\} \]](images/statug_glimmix0430.png)
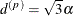
![\[ \mr{Cov}\left[\xi _ i,\xi _ j\right] = \ \sigma ^2\frac{1}{\Gamma (\nu )} \left(\frac{d_{ij}\sqrt {\nu }}{\rho }\right)^{\nu } 2 K_{\nu }\left(\frac{2d_{ij}\sqrt {\nu }}{\rho }\right) \]](images/statug_glimmix0432.png)
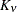
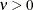

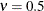
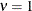
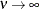
![\[ \mr{Cov}\left[\xi _ i,\xi _ j\right] = \sigma ^2 \rho ^{d_{ij}} \]](images/statug_glimmix0438.png)
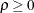
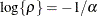
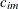
![\[ \mr{Cov}\left[\xi _ i,\xi _ j\right] = \sigma ^2 \rho _1^{|c_{i1} - c_{j1}|} \rho _2^{|c_{i2} - c_{j2}|} \ldots \rho _ k^{|c_{ik} - c_{jk}|} \]](images/statug_glimmix0442.png)
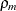
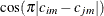
![\[ \mr{Cov}\left[\xi _ i,\xi _ j\right] = \left\{ \begin{array}{ll} \sigma ^2 \left\{ 1 - \frac{3 d_{ij}}{2 \alpha } + \frac{1}{2} \left(\frac{d_{ij}}{\alpha }\right)^3 \right\} & d_{ij} \leq \alpha \\ 0 & d_{ij} > \alpha \end{array} \right. \]](images/statug_glimmix0445.png)
![\[ \mr{Cov}\left[\xi _ i,\xi _ j\right] = \left\{ \begin{array}{ll} \sigma ^2 & i=j \\ \sigma _{|i-j|} & i \not= j \end{array} \right. \]](images/statug_glimmix0446.png)
![\[ \mr{Cov}\left[\xi _ i,\xi _ j\right] = \left\{ \begin{array}{ll} \sigma ^2 & i=j \\ \sigma _{|i-j|} & |i-j| < q \end{array} \right. \]](images/statug_glimmix0447.png)
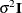
![\[ \mr{Cov}\left[\xi _ i,\xi _ j\right] = \left\{ \begin{array}{ll} \sigma ^2_ i & i = j \\ \rho _{|i-j|} \sqrt {\sigma ^2_ i \sigma ^2_ j} & i \not= j \end{array} \right. \]](images/statug_glimmix0449.png)
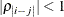
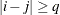
![\[ \mr{Cov}\left[\xi _ i,\xi _ j\right] = \sigma _{ij} \]](images/statug_glimmix0452.png)
![\[ \mr{Cov}\left[\xi _ i,\xi _ j\right] = \sigma _ i\sigma _ j\rho _{ij} \]](images/statug_glimmix0453.png)