The GLIMMIX Procedure
-
Overview

-
Getting Started

-
Syntax
 PROC GLIMMIX StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementCOVTEST StatementEFFECT StatementESTIMATE StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPARMS StatementRANDOM StatementSLICE StatementSTORE StatementWEIGHT StatementProgramming StatementsUser-Defined Link or Variance Function
PROC GLIMMIX StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementCOVTEST StatementEFFECT StatementESTIMATE StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPARMS StatementRANDOM StatementSLICE StatementSTORE StatementWEIGHT StatementProgramming StatementsUser-Defined Link or Variance Function -
Details
 Generalized Linear Models TheoryGeneralized Linear Mixed Models TheoryGLM Mode or GLMM ModeStatistical Inference for Covariance ParametersDegrees of Freedom MethodsEmpirical Covariance ("Sandwich") EstimatorsExploring and Comparing Covariance MatricesProcessing by SubjectsRadial Smoothing Based on Mixed ModelsOdds and Odds Ratio EstimationParameterization of Generalized Linear Mixed ModelsResponse-Level Ordering and ReferencingComparing the GLIMMIX and MIXED ProceduresSingly or Doubly Iterative FittingDefault Estimation TechniquesDefault OutputNotes on Output StatisticsODS Table NamesODS Graphics
Generalized Linear Models TheoryGeneralized Linear Mixed Models TheoryGLM Mode or GLMM ModeStatistical Inference for Covariance ParametersDegrees of Freedom MethodsEmpirical Covariance ("Sandwich") EstimatorsExploring and Comparing Covariance MatricesProcessing by SubjectsRadial Smoothing Based on Mixed ModelsOdds and Odds Ratio EstimationParameterization of Generalized Linear Mixed ModelsResponse-Level Ordering and ReferencingComparing the GLIMMIX and MIXED ProceduresSingly or Doubly Iterative FittingDefault Estimation TechniquesDefault OutputNotes on Output StatisticsODS Table NamesODS Graphics -
Examples
 Binomial Counts in Randomized BlocksMating Experiment with Crossed Random EffectsSmoothing Disease Rates; Standardized Mortality RatiosQuasi-likelihood Estimation for Proportions with Unknown DistributionJoint Modeling of Binary and Count DataRadial Smoothing of Repeated Measures DataIsotonic Contrasts for Ordered AlternativesAdjusted Covariance Matrices of Fixed EffectsTesting Equality of Covariance and Correlation MatricesMultiple Trends Correspond to Multiple Extrema in Profile LikelihoodsMaximum Likelihood in Proportional Odds Model with Random EffectsFitting a Marginal (GEE-Type) ModelResponse Surface Comparisons with Multiplicity AdjustmentsGeneralized Poisson Mixed Model for Overdispersed Count DataComparing Multiple B-SplinesDiallel Experiment with Multimember Random EffectsLinear Inference Based on Summary DataWeighted Multilevel Model for Survey DataQuadrature Method for Multilevel Model
Binomial Counts in Randomized BlocksMating Experiment with Crossed Random EffectsSmoothing Disease Rates; Standardized Mortality RatiosQuasi-likelihood Estimation for Proportions with Unknown DistributionJoint Modeling of Binary and Count DataRadial Smoothing of Repeated Measures DataIsotonic Contrasts for Ordered AlternativesAdjusted Covariance Matrices of Fixed EffectsTesting Equality of Covariance and Correlation MatricesMultiple Trends Correspond to Multiple Extrema in Profile LikelihoodsMaximum Likelihood in Proportional Odds Model with Random EffectsFitting a Marginal (GEE-Type) ModelResponse Surface Comparisons with Multiplicity AdjustmentsGeneralized Poisson Mixed Model for Overdispersed Count DataComparing Multiple B-SplinesDiallel Experiment with Multimember Random EffectsLinear Inference Based on Summary DataWeighted Multilevel Model for Survey DataQuadrature Method for Multilevel Model - References
Example 45.19 Quadrature Method for Multilevel Model
In many fields, data are observed on nested units at multiple levels. For example, in an educational study, classes of students from multiple schools might be assigned to one of two programs. At the end of the program, students take an evaluation test for which they receive a grade of Pass or Fail. Such a study has a three-level structure:
-
Students are the level-1 units.
-
Classes are the level-2 clusters.
-
Schools are the level-3 clusters.
Students are nested within classes, which are further nested within schools.
The following DATA step simulates such data for 500 students from five classes that are selected from 10 schools. The observations
of test results (Grade) are simulated from a logistic model, with the variable Program as a fixed effect and the variables School and Class as random effects. The random effects for School and Class are simulated with variances 16.0 and 4.0, respectively.
data test;
do school = 1 to 10;
schef = rannor(1234)*4;
do class = 1 to 5;
clsef = rannor(2345)*2;
program = ranbin(12345,1,.5);
do student = 1 to 10;
eta = 3 + program + schef + clsef ;
p = 1/(1+exp(-eta));
grade = ranbin(23456,1,p);
output;
end;
end;
end;
run;
The following statements use a three-point adaptive quadrature to estimate this three-level model:
proc glimmix data=test method = quad(qpoints=3); class school class program; model grade = program/s dist=binomial link=logit solution; random int /subject = school; random int /subject = class(school); run;
Output 45.19.1 shows the model information. Note that Gauss-Hermite quadrature is used for likelihood approximation.
Output 45.19.1: Model Information
| Model Information | |
|---|---|
| Data Set | WORK.TEST |
| Response Variable | grade |
| Response Distribution | Binomial |
| Link Function | Logit |
| Variance Function | Default |
| Variance Matrix Blocked By | school |
| Estimation Technique | Maximum Likelihood |
| Likelihood Approximation | Gauss-Hermite Quadrature |
| Degrees of Freedom Method | Containment |
The covariance parameter estimates and the solutions for fixed effects are shown in Output 45.19.2.
Output 45.19.2: Parameter Estimates
For this model, the number of random effects within each school is 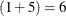 : one for school random intercept and five for random intercepts for classes that are nested within the school. This means
that the marginal log-likelihood computation requires the numerical evaluation of a six-dimensional integral. With the number
of quadrature points set to three by the QPOINTS=3 suboption, this numerical evaluation computes
: one for school random intercept and five for random intercepts for classes that are nested within the school. This means
that the marginal log-likelihood computation requires the numerical evaluation of a six-dimensional integral. With the number
of quadrature points set to three by the QPOINTS=3 suboption, this numerical evaluation computes 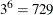 conditional log likelihoods for each observation on each pass through the data.
conditional log likelihoods for each observation on each pass through the data.
The number of conditional log likelihoods increases exponentially with the number of random effects. For example, suppose
that you increase the number of classes from five to ten. Then the number of conditional log-likelihood evaluations becomes
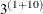 = 177,147 for each observation, where 1 is the number of random school intercepts and 10 is the number of random intercepts
for classes that are nested within each school. In many applications, it is not uncommon to have more than 10 nested units
within a higher-level unit. As the number of nested units increases, the number of nested random effects increases, driving
the exponential growth of the computational requirement.
= 177,147 for each observation, where 1 is the number of random school intercepts and 10 is the number of random intercepts
for classes that are nested within each school. In many applications, it is not uncommon to have more than 10 nested units
within a higher-level unit. As the number of nested units increases, the number of nested random effects increases, driving
the exponential growth of the computational requirement.
To address the intimidating computational demand for dealing with such multilevel models, Pinheiro and Chao (2006) propose a multilevel adaptive quadrature algorithm. You can use the FASTQUAD suboption in the METHOD=QUAD option to invoke this algorithm. The following DATA step simulates the data set for 10 schools:
data test;
do school = 1 to 10;
schef = rannor(1234)*4;
do class = 1 to 10;
clsef = rannor(2345)*2;
program = ranbin(12345,1,.5);
do student = 1 to 10;
eta = 3 + program + schef + clsef ;
p = 1/(1+exp(-eta));
grade = ranbin(23456,1,p);
output;
end;
end;
end;
run;
The following statements use the FASTQUAD suboption to request multilevel quadrature estimation for the model:
proc glimmix data=test method = quad(qpoints=3 fastquad); class school class program; model grade = program/s dist=binomial link=logit solution; random int /subject = school; random int /subject = class(school); run;
The "Model Information" table in Output 45.19.3 shows that multilevel Gauss-Hermite quadrature is used for likelihood approximation.
Output 45.19.3: Model Information
| Model Information | |
|---|---|
| Data Set | WORK.TEST |
| Response Variable | grade |
| Response Distribution | Binomial |
| Link Function | Logit |
| Variance Function | Default |
| Variance Matrix Blocked By | school |
| Estimation Technique | Maximum Likelihood |
| Likelihood Approximation | Multilevel Gauss-Hermite Quadrature |
| Degrees of Freedom Method | Containment |
Output 45.19.3 displays the parameter estimates.
Output 45.19.4: Parameter Estimates
In multilevel quadrature, the number of random effects within each school is 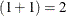 : one for the school random intercept and one for the class random intercept. That is, the number of class random intercepts
does not grow with the number of classes. With three quadrature points, this leads to
: one for the school random intercept and one for the class random intercept. That is, the number of class random intercepts
does not grow with the number of classes. With three quadrature points, this leads to 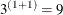 evaluations of conditional log likelihoods for any number of classes in this example. In addition to reducing computational
demand, multilevel adaptive quadrature also reduces memory usage. Both the computational efficiency and the memory-usage efficiency
that the FASTQUAD suboption affords enables you to handle much larger multilevel models.
evaluations of conditional log likelihoods for any number of classes in this example. In addition to reducing computational
demand, multilevel adaptive quadrature also reduces memory usage. Both the computational efficiency and the memory-usage efficiency
that the FASTQUAD suboption affords enables you to handle much larger multilevel models.