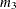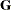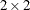-
HOLD=value-list
-
specifies which parameter values PROC GLIMMIX should hold equal to the
specified values. For example, the following statement constrains the first and third covariance parameters to equal 5 and
2, respectively:
parms (5) (3) (2) (3) / hold=1,3;
Covariance or
scale parameters that are held fixed with the HOLD= option are treated as constrained parameters in the optimization. This
is different from evaluating the objective function, gradient, and Hessian matrix at known values of the covariance parameters.
A constrained parameter introduces a singularity in the optimization process. The covariance matrix of the covariance parameters
(see the ASYCOV
option of the PROC GLIMMIX
statement) is then based on the projected Hessian matrix. As a consequence, the variance of parameters subjected to a HOLD=
is zero. Such parameters do not contribute to the computation of denominator degrees of freedom with the DDFM=
KENWARDROGER and DDFM=
SATTERTHWAITE methods, for example. If you want to treat the covariance parameters as known, without imposing constraints
on the optimization, you should use the NOITER
option.
When you place a hold on all parameters (or when you specify the NOITER) option in a GLMM, you might notice that PROC GLIMMIX
continues to produce an iteration history. Unless your model is a linear mixed model, several recomputations of the pseudo-response
might be required in linearization-based methods to achieve agreement between the pseudo-data and the covariance matrix. In
other words, the GLIMMIX procedure continues to update the fixed-effects estimates (and random-effects solutions) until convergence
is achieved.
In certain models, placing a hold on covariance parameters implies that the procedure processes the parameters in the same
order as if the NOPROFILE
were in effect. This can change the order of the covariance parameters when you place a hold on one or more parameters. Models
that are subject to this reordering are those with
R-side covariance structures whose scale parameter could be profiled. This includes the TYPE=CS
, TYPE=SP
, TYPE=AR(1)
, TYPE=TOEP
, and TYPE=ARMA(1,1)
covariance structures.
-
LOWERB=value-list
-
enables you to specify lower boundary constraints for the covariance
or scale parameters. The value-list specification is a list of numbers or missing values (.) separated by commas. You must list the numbers in the same order
that PROC GLIMMIX uses for the value-list in the PARMS statement, and each number corresponds to the lower boundary constraint. A missing value instructs PROC GLIMMIX
to use its default constraint, and if you do not specify numbers for all of the covariance parameters, PROC GLIMMIX assumes
that the remaining ones are missing.
This option is useful, for example, when you want to constrain the 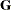 matrix to be positive definite in order to avoid the more computationally intensive algorithms required when
matrix to be positive definite in order to avoid the more computationally intensive algorithms required when 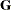 becomes singular. The corresponding statements for a random coefficients model are as follows:
becomes singular. The corresponding statements for a random coefficients model are as follows:
proc glimmix;
class person;
model y = time;
random int time / type=chol sub=person;
parms / lowerb=1e-4,.,1e-4;
run;
Here, the TYPE=CHOL
structure is used in order to specify a Cholesky root parameterization for the 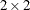 unstructured blocks in
unstructured blocks in 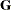 . This parameterization ensures that the
. This parameterization ensures that the 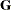 matrix is nonnegative definite, and the PARMS statement then ensures that it is positive definite by constraining the two
diagonal terms to be greater than or equal to 1E–4.
matrix is nonnegative definite, and the PARMS statement then ensures that it is positive definite by constraining the two
diagonal terms to be greater than or equal to 1E–4.
-
NOBOUND
-
requests the removal of boundary constraints on covariance
and scale parameters in mixed models. For example, variance components have a default lower boundary constraint of 0, and
the NOBOUND option allows their estimates to be negative. See the NOBOUND
option in the PROC GLIMMIX
statement for further details.
-
NOITER
-
requests that no optimization of the covariance parameters be
performed. This option has no effect in generalized linear models.
If you specify the NOITER option, PROC GLIMMIX uses the values for the covariance parameters given in the PARMS statement
to perform statistical inferences. Note that the NOITER option is not equivalent to specifying a HOLD=
value for all covariance parameters. If you use the NOITER option, covariance parameters are not constrained in the optimization.
This prevents singularities that might otherwise occur in the optimization process.
If a residual variance is profiled, the parameter estimates can change from the initial values you provide as the residual
variance is recomputed. To prevent an update of the residual variance, combine the NOITER option with the NOPROFILE
option in the PROC GLIMMIX
statements, as in the following code:
proc glimmix noprofile;
class A B C rep mp sp;
model y = A | B | C;
random rep mp sp;
parms (180) (200) (170) (1000) / noiter;
run;
When you specify the NOITER option in a model where parameters are estimated by pseudo-likelihood techniques, you might notice
that the GLIMMIX procedure continues to produce an iteration history. Unless your model is a linear mixed model, several recomputations
of the pseudo-response might be required in linearization-based methods to achieve agreement between the pseudo-data and the
covariance matrix. In other words, the GLIMMIX procedure continues to update the profiled fixed-effects estimates (and random-effects
solutions) until convergence is achieved. To prevent these updates, use the MAXLMMUPDATE=
option in the PROC GLIMMIX
statement. Specifying the NOITER option in the PARMS statement of a GLMM with pseudo-likelihood estimation has the same effect
as choosing TECHNIQUE=NONE in the NLOPTIONS
statement.
If you want to base initial fixed-effects estimates on the results of fitting a generalized linear model, then you can combine
the NOITER option with the TECHNIQUE= option. For example, the following statements determine the starting values for the
fixed effects by fitting a logistic model (without random effects) with the Newton-Raphson algorithm:
proc glimmix startglm inititer=10;
class clinic A;
model y/n = A / link=logit dist=binomial;
random clinic;
parms (0.4) / noiter;
nloptions technique=newrap;
run;
The initial GLM fit stops at convergence or after at most 10 iterations, whichever comes first. The pseudo-data for the linearized
GLMM is computed from the GLM estimates. The variance of the Clinic random effect is held constant at 0.4 during subsequent iterations that update the fixed effects only.
If you also want to combine the GLM fixed-effects estimates with known and fixed covariance parameter values without updating
the fixed effects, you can add the MAXLMMUPDATE
=0 option:
proc glimmix startglm inititer=10 maxlmmupdate=0;
class clinic A;
model y/n = A / link=logit dist=binomial;
random clinic;
parms (0.4) / noiter;
nloptions technique=newrap;
run;
In a GLMM with parameter estimation by METHOD=
LAPLACE
or METHOD=
QUAD
the NOITER option also leads to an iteration history, since the fixed-effects estimates are part of the optimization and
the PARMS statement places restrictions on only the covariance parameters.
Finally, the NOITER option can be useful if you want to obtain minimum variance quadratic unbiased estimates (with 0 priors),
also known as MIVQUE0 estimates (Goodnight 1978a). Because MIVQUE0 estimates are starting values for covariance parameters—unless you provide (value-list) in the PARMS statement—the following statements produce MIVQUE0 mixed model estimates:
proc glimmix noprofile;
class A B;
model y = A;
random int / subject=B;
parms / noiter;
run;
-
PARMSDATA=SAS-data-set
PDATA=SAS-data-set
-
reads in covariance parameter values from a SAS data set. The data
set should contain the numerical variable ESTIMATE or the numerical variables Covp1–Covpq, where q denotes the number of covariance parameters.
If the PARMSDATA= data set contains multiple sets of covariance parameters, the GLIMMIX procedure evaluates the initial objective
function for each set and commences the optimization step by using the set with the lowest function value as the starting
values. For example, the following SAS statements request that the objective function be evaluated for three sets of initial
values:
data data_covp;
input covp1-covp4;
datalines;
180 200 170 1000
170 190 160 900
160 180 150 800
;
proc glimmix;
class A B C rep mainEU smallEU;
model yield = A|B|C;
random rep mainEU smallEU;
parms / pdata=data_covp;
run;
Each set comprises four covariance parameters.
The order of the observations in a data set with the numerical variable Estimate corresponds to the order of the covariance parameters in the "Covariance Parameter Estimates" table. In a GLM, the PARMSDATA=
option can be used to set the starting value for the exponential family
scale parameter. A grid search is not conducted for GLMs if you specify multiple values.
The PARMSDATA= data set must not contain missing values.
If the GLIMMIX procedure is processing the input data set in BY
groups, you can add the BY variables to the PARMSDATA= data set. If this data set is sorted by the BY variables, the GLIMMIX
procedure matches the covariance parameter values to the current BY group. If the PARMSDATA= data set does not contain all
BY variables, the data set is processed in its entirety for every BY group and a message is written to the log. This enables
you to provide a single set of starting values across BY groups, as in the following statements:
data data_covp;
input covp1-covp4;
datalines;
180 200 170 1000
;
proc glimmix;
class A B C rep mainEU smallEU;
model yield = A|B|C;
random rep mainEU smallEU;
parms / pdata=data_covp;
by year;
run;
The same set of starting values is used for each value of the year variable.
-
UPPERB=value-list
-
enables you to specify upper boundary constraints on the covariance
parameters. The value-list specification is a list of numbers or missing values (.) separated by commas. You must list the numbers in the same order
that PROC GLIMMIX uses for the value-list in the PARMS statement, and each number corresponds to the upper boundary constraint. A missing value instructs PROC GLIMMIX
to use its default constraint. If you do not specify numbers for all of the covariance parameters, PROC GLIMMIX assumes that
the remaining ones are missing.


 PROC GLIMMIX StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementCOVTEST StatementEFFECT StatementESTIMATE StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPARMS StatementRANDOM StatementSLICE StatementSTORE StatementWEIGHT StatementProgramming StatementsUser-Defined Link or Variance Function
PROC GLIMMIX StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementCOVTEST StatementEFFECT StatementESTIMATE StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPARMS StatementRANDOM StatementSLICE StatementSTORE StatementWEIGHT StatementProgramming StatementsUser-Defined Link or Variance Function Generalized Linear Models TheoryGeneralized Linear Mixed Models TheoryGLM Mode or GLMM ModeStatistical Inference for Covariance ParametersDegrees of Freedom MethodsEmpirical Covariance ("Sandwich") EstimatorsExploring and Comparing Covariance MatricesProcessing by SubjectsRadial Smoothing Based on Mixed ModelsOdds and Odds Ratio EstimationParameterization of Generalized Linear Mixed ModelsResponse-Level Ordering and ReferencingComparing the GLIMMIX and MIXED ProceduresSingly or Doubly Iterative FittingDefault Estimation TechniquesDefault OutputNotes on Output StatisticsODS Table NamesODS Graphics
Generalized Linear Models TheoryGeneralized Linear Mixed Models TheoryGLM Mode or GLMM ModeStatistical Inference for Covariance ParametersDegrees of Freedom MethodsEmpirical Covariance ("Sandwich") EstimatorsExploring and Comparing Covariance MatricesProcessing by SubjectsRadial Smoothing Based on Mixed ModelsOdds and Odds Ratio EstimationParameterization of Generalized Linear Mixed ModelsResponse-Level Ordering and ReferencingComparing the GLIMMIX and MIXED ProceduresSingly or Doubly Iterative FittingDefault Estimation TechniquesDefault OutputNotes on Output StatisticsODS Table NamesODS Graphics Binomial Counts in Randomized BlocksMating Experiment with Crossed Random EffectsSmoothing Disease Rates; Standardized Mortality RatiosQuasi-likelihood Estimation for Proportions with Unknown DistributionJoint Modeling of Binary and Count DataRadial Smoothing of Repeated Measures DataIsotonic Contrasts for Ordered AlternativesAdjusted Covariance Matrices of Fixed EffectsTesting Equality of Covariance and Correlation MatricesMultiple Trends Correspond to Multiple Extrema in Profile LikelihoodsMaximum Likelihood in Proportional Odds Model with Random EffectsFitting a Marginal (GEE-Type) ModelResponse Surface Comparisons with Multiplicity AdjustmentsGeneralized Poisson Mixed Model for Overdispersed Count DataComparing Multiple B-SplinesDiallel Experiment with Multimember Random EffectsLinear Inference Based on Summary DataWeighted Multilevel Model for Survey DataQuadrature Method for Multilevel Model
Binomial Counts in Randomized BlocksMating Experiment with Crossed Random EffectsSmoothing Disease Rates; Standardized Mortality RatiosQuasi-likelihood Estimation for Proportions with Unknown DistributionJoint Modeling of Binary and Count DataRadial Smoothing of Repeated Measures DataIsotonic Contrasts for Ordered AlternativesAdjusted Covariance Matrices of Fixed EffectsTesting Equality of Covariance and Correlation MatricesMultiple Trends Correspond to Multiple Extrema in Profile LikelihoodsMaximum Likelihood in Proportional Odds Model with Random EffectsFitting a Marginal (GEE-Type) ModelResponse Surface Comparisons with Multiplicity AdjustmentsGeneralized Poisson Mixed Model for Overdispersed Count DataComparing Multiple B-SplinesDiallel Experiment with Multimember Random EffectsLinear Inference Based on Summary DataWeighted Multilevel Model for Survey DataQuadrature Method for Multilevel Model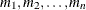
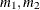 to
to