The GLIMMIX Procedure
-
Overview

-
Getting Started

-
Syntax
 PROC GLIMMIX StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementCOVTEST StatementEFFECT StatementESTIMATE StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPARMS StatementRANDOM StatementSLICE StatementSTORE StatementWEIGHT StatementProgramming StatementsUser-Defined Link or Variance Function
PROC GLIMMIX StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementCOVTEST StatementEFFECT StatementESTIMATE StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPARMS StatementRANDOM StatementSLICE StatementSTORE StatementWEIGHT StatementProgramming StatementsUser-Defined Link or Variance Function -
Details
 Generalized Linear Models TheoryGeneralized Linear Mixed Models TheoryGLM Mode or GLMM ModeStatistical Inference for Covariance ParametersDegrees of Freedom MethodsEmpirical Covariance ("Sandwich") EstimatorsExploring and Comparing Covariance MatricesProcessing by SubjectsRadial Smoothing Based on Mixed ModelsOdds and Odds Ratio EstimationParameterization of Generalized Linear Mixed ModelsResponse-Level Ordering and ReferencingComparing the GLIMMIX and MIXED ProceduresSingly or Doubly Iterative FittingDefault Estimation TechniquesDefault OutputNotes on Output StatisticsODS Table NamesODS Graphics
Generalized Linear Models TheoryGeneralized Linear Mixed Models TheoryGLM Mode or GLMM ModeStatistical Inference for Covariance ParametersDegrees of Freedom MethodsEmpirical Covariance ("Sandwich") EstimatorsExploring and Comparing Covariance MatricesProcessing by SubjectsRadial Smoothing Based on Mixed ModelsOdds and Odds Ratio EstimationParameterization of Generalized Linear Mixed ModelsResponse-Level Ordering and ReferencingComparing the GLIMMIX and MIXED ProceduresSingly or Doubly Iterative FittingDefault Estimation TechniquesDefault OutputNotes on Output StatisticsODS Table NamesODS Graphics -
Examples
 Binomial Counts in Randomized BlocksMating Experiment with Crossed Random EffectsSmoothing Disease Rates; Standardized Mortality RatiosQuasi-likelihood Estimation for Proportions with Unknown DistributionJoint Modeling of Binary and Count DataRadial Smoothing of Repeated Measures DataIsotonic Contrasts for Ordered AlternativesAdjusted Covariance Matrices of Fixed EffectsTesting Equality of Covariance and Correlation MatricesMultiple Trends Correspond to Multiple Extrema in Profile LikelihoodsMaximum Likelihood in Proportional Odds Model with Random EffectsFitting a Marginal (GEE-Type) ModelResponse Surface Comparisons with Multiplicity AdjustmentsGeneralized Poisson Mixed Model for Overdispersed Count DataComparing Multiple B-SplinesDiallel Experiment with Multimember Random EffectsLinear Inference Based on Summary DataWeighted Multilevel Model for Survey DataQuadrature Method for Multilevel Model
Binomial Counts in Randomized BlocksMating Experiment with Crossed Random EffectsSmoothing Disease Rates; Standardized Mortality RatiosQuasi-likelihood Estimation for Proportions with Unknown DistributionJoint Modeling of Binary and Count DataRadial Smoothing of Repeated Measures DataIsotonic Contrasts for Ordered AlternativesAdjusted Covariance Matrices of Fixed EffectsTesting Equality of Covariance and Correlation MatricesMultiple Trends Correspond to Multiple Extrema in Profile LikelihoodsMaximum Likelihood in Proportional Odds Model with Random EffectsFitting a Marginal (GEE-Type) ModelResponse Surface Comparisons with Multiplicity AdjustmentsGeneralized Poisson Mixed Model for Overdispersed Count DataComparing Multiple B-SplinesDiallel Experiment with Multimember Random EffectsLinear Inference Based on Summary DataWeighted Multilevel Model for Survey DataQuadrature Method for Multilevel Model - References
Example 45.16 Diallel Experiment with Multimember Random Effects
Cockerham and Weir (1977) apply variance component models in the analysis of reciprocal crosses. In these experiments, it is of interest to separate genetically determined variation from variation determined by parentage. This example analyzes the data for the diallel experiment in Cockerham and Weir (1977, Appendix C). A diallel is a mating design that consists of all possible crosses of a set of parental lines. It includes reciprocal crossings, but not self-crossings.
The basic model for a cross is 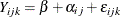 , where
, where 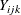 is the observation for offspring k from maternal parent i and paternal parent j. The various models in Cockerham and Weir (1977) are different decompositions of the term
is the observation for offspring k from maternal parent i and paternal parent j. The various models in Cockerham and Weir (1977) are different decompositions of the term 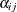 , the total effect that is due to the parents. Their "bio model" (model (c)) decomposes
, the total effect that is due to the parents. Their "bio model" (model (c)) decomposes 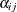 into
into
![\[ \alpha _{ij} = \eta _ i + \eta _ j + \mu _ i + \phi _ j + (\eta \eta )_{ij} + \kappa _{ij} \]](images/statug_glimmix1089.png)
where 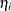 and
and 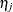 are contributions of the female and male parents, respectively. The term
are contributions of the female and male parents, respectively. The term 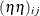 captures the interaction between maternal and paternal effects. In contrast to usual interaction effects, this term must
obey a symmetry because of the reciprocals:
captures the interaction between maternal and paternal effects. In contrast to usual interaction effects, this term must
obey a symmetry because of the reciprocals: 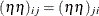 . The terms
. The terms 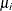 and
and 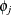 in the decomposition are extranuclear maternal and paternal effects, and the remaining interactions are captured by the
in the decomposition are extranuclear maternal and paternal effects, and the remaining interactions are captured by the 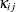 term.
term.
The following DATA step creates a SAS data set for the diallel example in Appendix C of Cockerham and Weir (1977):
data diallel;
label time = 'Flowering time in days';
do p = 1 to 8;
do m = 1 to 8;
if (m ne p) then do;
sym = trim(left(min(m,p))) || ',' || trim(left(max(m,p)));
do block = 1 to 2;
input time @@;
output;
end;
end;
end;
end;
datalines;
14.4 16.2 27.2 30.8 17.2 27.0 18.3 20.2 16.2 16.8 18.6 14.4 16.4 16.0
15.4 16.5 14.8 14.6 18.6 18.6 15.2 15.3 17.0 15.2 14.4 14.8 10.8 13.2
31.8 30.4 21.0 23.0 24.6 25.4 19.2 20.0 29.8 28.4 12.8 14.2 13.0 14.4
16.2 17.8 11.4 13.0 16.8 16.3 12.4 14.2 16.8 14.8 12.6 12.2 9.6 11.2
14.6 18.8 12.2 13.6 15.2 15.4 15.2 13.8 18.0 16.0 10.4 12.2 13.4 20.0
20.2 23.4 14.2 14.0 18.6 14.8 22.2 17.0 14.3 17.3 9.0 10.2 11.8 12.8
14.0 16.6 12.2 9.2 13.6 16.2 13.8 14.4 15.6 15.6 15.6 11.0 13.0 9.8
15.2 17.2 10.0 11.6 17.0 18.2 20.8 20.8 20.0 17.4 17.0 12.6 13.0 9.8
;
The observations represent mean flowering times of Nicotiana rustica (Aztec tobacco) from crosses of inbred varieties grown in two blocks. The variables p and m identify the eight paternal and maternal lines, respectively. The variable sym is used to model the interaction between the parents, subject to the symmetry condition 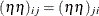 . For example, the first two observations, 14.4 and 16.2 days, represent the observations from blocks 1 and 2 where paternal
line 1 was crossed with maternal line 2.
. For example, the first two observations, 14.4 and 16.2 days, represent the observations from blocks 1 and 2 where paternal
line 1 was crossed with maternal line 2.
The following PROC GLIMMIX statements fit the "bio model" in Cockerham and Weir (1977):
proc glimmix data=diallel outdesign(z)=zmat; class block sym p m; effect line = mm(p m); model time = block; random line sym p m p*m; run;
The EFFECT
statement defines the nuclear parental contributions as a multimember effect based on the CLASS
variables p and m. Each observation has two nonzero entries in the design matrix for the effect that identifies the paternal and maternal lines.
The terms in the RANDOM
statement model the variance components as follows: line 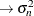 ,
, sym 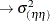 ,
, p 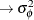 ,
, m 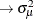 ,
, p*m 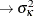 . The OUTDESIGN=
option in the PROC GLIMMIX
statement writes the
. The OUTDESIGN=
option in the PROC GLIMMIX
statement writes the 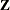 matrix to the SAS data set
matrix to the SAS data set zmat. The EFFECT statement alleviates the need for complex coding, as in Section 2.3 of Saxton (2004).
Output 45.16.1 displays the "Class Level Information" table of the diallel model. Because the interaction terms are symmetric, there are
only 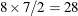 levels for the 8 lines. The estimates of the variance components and the residual variance in Output 45.16.1 agree with the results in Table 7 of Cockerham and Weir (1977).
levels for the 8 lines. The estimates of the variance components and the residual variance in Output 45.16.1 agree with the results in Table 7 of Cockerham and Weir (1977).
Output 45.16.1: Class Levels and Covariance Parameter Estimates in Diallel Example
The following statements print the 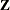 matrix columns that correspond to the multimember
matrix columns that correspond to the multimember line effect for the first 10 observations in block 1 (Output 45.16.2). For each observation there are two nonzero entries, and their column index corresponds to the index of the paternal and
maternal line.
proc print data=zmat(where=(block=1) obs=10); var p m time _z1-_z8; run;
Output 45.16.2: Z Matrix for Line Effect of the First 10 Observations in Block 1
| Obs | p | m | time | _Z1 | _Z2 | _Z3 | _Z4 | _Z5 | _Z6 | _Z7 | _Z8 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 14.4 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 1 | 3 | 27.2 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 5 | 1 | 4 | 17.2 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 7 | 1 | 5 | 18.3 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 9 | 1 | 6 | 16.2 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 11 | 1 | 7 | 18.6 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 13 | 1 | 8 | 16.4 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 15 | 2 | 1 | 15.4 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 17 | 2 | 3 | 14.8 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 19 | 2 | 4 | 18.6 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |