The GLIMMIX Procedure
-
Overview

-
Getting Started

-
Syntax
 PROC GLIMMIX StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementCOVTEST StatementEFFECT StatementESTIMATE StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPARMS StatementRANDOM StatementSLICE StatementSTORE StatementWEIGHT StatementProgramming StatementsUser-Defined Link or Variance Function
PROC GLIMMIX StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementCOVTEST StatementEFFECT StatementESTIMATE StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPARMS StatementRANDOM StatementSLICE StatementSTORE StatementWEIGHT StatementProgramming StatementsUser-Defined Link or Variance Function -
Details
 Generalized Linear Models TheoryGeneralized Linear Mixed Models TheoryGLM Mode or GLMM ModeStatistical Inference for Covariance ParametersDegrees of Freedom MethodsEmpirical Covariance ("Sandwich") EstimatorsExploring and Comparing Covariance MatricesProcessing by SubjectsRadial Smoothing Based on Mixed ModelsOdds and Odds Ratio EstimationParameterization of Generalized Linear Mixed ModelsResponse-Level Ordering and ReferencingComparing the GLIMMIX and MIXED ProceduresSingly or Doubly Iterative FittingDefault Estimation TechniquesDefault OutputNotes on Output StatisticsODS Table NamesODS Graphics
Generalized Linear Models TheoryGeneralized Linear Mixed Models TheoryGLM Mode or GLMM ModeStatistical Inference for Covariance ParametersDegrees of Freedom MethodsEmpirical Covariance ("Sandwich") EstimatorsExploring and Comparing Covariance MatricesProcessing by SubjectsRadial Smoothing Based on Mixed ModelsOdds and Odds Ratio EstimationParameterization of Generalized Linear Mixed ModelsResponse-Level Ordering and ReferencingComparing the GLIMMIX and MIXED ProceduresSingly or Doubly Iterative FittingDefault Estimation TechniquesDefault OutputNotes on Output StatisticsODS Table NamesODS Graphics -
Examples
 Binomial Counts in Randomized BlocksMating Experiment with Crossed Random EffectsSmoothing Disease Rates; Standardized Mortality RatiosQuasi-likelihood Estimation for Proportions with Unknown DistributionJoint Modeling of Binary and Count DataRadial Smoothing of Repeated Measures DataIsotonic Contrasts for Ordered AlternativesAdjusted Covariance Matrices of Fixed EffectsTesting Equality of Covariance and Correlation MatricesMultiple Trends Correspond to Multiple Extrema in Profile LikelihoodsMaximum Likelihood in Proportional Odds Model with Random EffectsFitting a Marginal (GEE-Type) ModelResponse Surface Comparisons with Multiplicity AdjustmentsGeneralized Poisson Mixed Model for Overdispersed Count DataComparing Multiple B-SplinesDiallel Experiment with Multimember Random EffectsLinear Inference Based on Summary DataWeighted Multilevel Model for Survey DataQuadrature Method for Multilevel Model
Binomial Counts in Randomized BlocksMating Experiment with Crossed Random EffectsSmoothing Disease Rates; Standardized Mortality RatiosQuasi-likelihood Estimation for Proportions with Unknown DistributionJoint Modeling of Binary and Count DataRadial Smoothing of Repeated Measures DataIsotonic Contrasts for Ordered AlternativesAdjusted Covariance Matrices of Fixed EffectsTesting Equality of Covariance and Correlation MatricesMultiple Trends Correspond to Multiple Extrema in Profile LikelihoodsMaximum Likelihood in Proportional Odds Model with Random EffectsFitting a Marginal (GEE-Type) ModelResponse Surface Comparisons with Multiplicity AdjustmentsGeneralized Poisson Mixed Model for Overdispersed Count DataComparing Multiple B-SplinesDiallel Experiment with Multimember Random EffectsLinear Inference Based on Summary DataWeighted Multilevel Model for Survey DataQuadrature Method for Multilevel Model - References
ESTIMATE Statement
-
ESTIMATE 'label' contrast-specification <(divisor=n)><, 'label' contrast-specification <(divisor=n)>> <, …> </ options>;
The ESTIMATE statement provides a mechanism for obtaining custom hypothesis tests. As in the CONTRAST statement, the basic element of the ESTIMATE statement is the contrast-specification, which consists of MODEL and G-side random effects and their coefficients. Specifically, a contrast-specification takes the form
< fixed-effect values …> < | random-effect values …>
Based on the contrast-specifications in your ESTIMATE statement, PROC GLIMMIX constructs the matrix ![$\bL ’ = [\bK ’ \bM ’]$](images/statug_glimmix0170.png) , as in the CONTRAST
statement, where
, as in the CONTRAST
statement, where 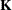 is associated with the fixed effects and
is associated with the fixed effects and 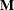 is associated with the G-side random effects. The GLIMMIX procedure supports nonpositional syntax for the coefficients of
fixed effects in the ESTIMATE statement. For details see the section Positional and Nonpositional Syntax for Contrast Coefficients.
is associated with the G-side random effects. The GLIMMIX procedure supports nonpositional syntax for the coefficients of
fixed effects in the ESTIMATE statement. For details see the section Positional and Nonpositional Syntax for Contrast Coefficients.
PROC GLIMMIX then produces for each row 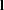 of
of 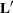 an approximate t test of the hypothesis
an approximate t test of the hypothesis 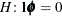 , where
, where ![$\bphi = [\bbeta ’\ \bgamma ’]’$](images/statug_glimmix0174.png) . You can also obtain multiplicity-adjusted p-values and confidence limits for multirow estimates with the ADJUST=
option. The output from multiple ESTIMATE statements is organized as follows. Results from unadjusted estimates are reported
first in a single table, followed by separate tables for each of the adjusted estimates. Results from all ESTIMATE statements
are combined in the "Estimates" ODS table.
. You can also obtain multiplicity-adjusted p-values and confidence limits for multirow estimates with the ADJUST=
option. The output from multiple ESTIMATE statements is organized as follows. Results from unadjusted estimates are reported
first in a single table, followed by separate tables for each of the adjusted estimates. Results from all ESTIMATE statements
are combined in the "Estimates" ODS table.
Note that multirow estimates are permitted. Unlike the CONTRAST statement, you need to specify a 'label' for every row of the multirow estimate, because PROC GLIMMIX produces one test per row. PROC GLIMMIX selects the degrees of freedom to match those displayed in the "Type III Tests of Fixed Effects" table for the final effect you list in the ESTIMATE statement. You can modify the degrees of freedom by using the DF= option. If you select DDFM =NONE and do not modify the degrees of freedom by using the DF= option, PROC GLIMMIX uses infinite degrees of freedom, essentially computing approximate z tests. If PROC GLIMMIX finds the fixed-effects portion of the specified estimate to be nonestimable, then it displays "Non-est" for the estimate entry.
Table 45.7 summarizes the options available in the ESTIMATE statement.
Table 45.7: ESTIMATE Statement Options
|
Option |
Description |
|---|---|
|
Construction and Computation of Estimable Functions |
|
|
Specifies a list of values to divide the coefficients |
|
|
Sets up random-effect contrasts between different groups |
|
|
Tunes the estimability checking difference |
|
|
Sets up random-effect contrasts between different subjects |
|
|
Degrees of Freedom and p-values |
|
|
Determines denominator degrees of freedom when p-values and confidence limits are adjusted for multiple comparisons |
|
|
Determines the method for multiple comparison adjustment of estimates |
|
|
Determines the confidence level ( |
|
|
Assigns a specific value to degrees of freedom for tests and confidence limits |
|
|
Performs one-sided, lower-tailed inference |
|
|
Adjusts multiplicity-corrected p-values further in a step-down fashion |
|
|
Performs one-sided, upper-tailed inference |
|
|
Statistical Output |
|
|
Constructs t-type confidence limits |
|
|
Prints the |
|
|
Generalized Linear Modeling |
|
|
Reports estimates separately for each category for models with nominal data |
|
|
Displays exponentiated estimates |
|
|
Computes and displays estimates and standard errors on the inverse linked scale |
|

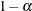


![\[ \frac{1}{1+\exp \{ -(\alpha _1 - \alpha _2)\} } \]](images/statug_glimmix0176.png)
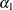
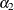
![\[ \pi _1 - \pi _2 = \frac{1}{1+\exp \{ -\beta _0 - \alpha _1\} } - \frac{1}{1+\exp \{ -\beta _0 - \alpha _2\} } \]](images/statug_glimmix0179.png)