The GLIMMIX Procedure
-
Overview

-
Getting Started

-
Syntax
 PROC GLIMMIX StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementCOVTEST StatementEFFECT StatementESTIMATE StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPARMS StatementRANDOM StatementSLICE StatementSTORE StatementWEIGHT StatementProgramming StatementsUser-Defined Link or Variance Function
PROC GLIMMIX StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementCOVTEST StatementEFFECT StatementESTIMATE StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPARMS StatementRANDOM StatementSLICE StatementSTORE StatementWEIGHT StatementProgramming StatementsUser-Defined Link or Variance Function -
Details
 Generalized Linear Models TheoryGeneralized Linear Mixed Models TheoryGLM Mode or GLMM ModeStatistical Inference for Covariance ParametersDegrees of Freedom MethodsEmpirical Covariance ("Sandwich") EstimatorsExploring and Comparing Covariance MatricesProcessing by SubjectsRadial Smoothing Based on Mixed ModelsOdds and Odds Ratio EstimationParameterization of Generalized Linear Mixed ModelsResponse-Level Ordering and ReferencingComparing the GLIMMIX and MIXED ProceduresSingly or Doubly Iterative FittingDefault Estimation TechniquesDefault OutputNotes on Output StatisticsODS Table NamesODS Graphics
Generalized Linear Models TheoryGeneralized Linear Mixed Models TheoryGLM Mode or GLMM ModeStatistical Inference for Covariance ParametersDegrees of Freedom MethodsEmpirical Covariance ("Sandwich") EstimatorsExploring and Comparing Covariance MatricesProcessing by SubjectsRadial Smoothing Based on Mixed ModelsOdds and Odds Ratio EstimationParameterization of Generalized Linear Mixed ModelsResponse-Level Ordering and ReferencingComparing the GLIMMIX and MIXED ProceduresSingly or Doubly Iterative FittingDefault Estimation TechniquesDefault OutputNotes on Output StatisticsODS Table NamesODS Graphics -
Examples
 Binomial Counts in Randomized BlocksMating Experiment with Crossed Random EffectsSmoothing Disease Rates; Standardized Mortality RatiosQuasi-likelihood Estimation for Proportions with Unknown DistributionJoint Modeling of Binary and Count DataRadial Smoothing of Repeated Measures DataIsotonic Contrasts for Ordered AlternativesAdjusted Covariance Matrices of Fixed EffectsTesting Equality of Covariance and Correlation MatricesMultiple Trends Correspond to Multiple Extrema in Profile LikelihoodsMaximum Likelihood in Proportional Odds Model with Random EffectsFitting a Marginal (GEE-Type) ModelResponse Surface Comparisons with Multiplicity AdjustmentsGeneralized Poisson Mixed Model for Overdispersed Count DataComparing Multiple B-SplinesDiallel Experiment with Multimember Random EffectsLinear Inference Based on Summary DataWeighted Multilevel Model for Survey DataQuadrature Method for Multilevel Model
Binomial Counts in Randomized BlocksMating Experiment with Crossed Random EffectsSmoothing Disease Rates; Standardized Mortality RatiosQuasi-likelihood Estimation for Proportions with Unknown DistributionJoint Modeling of Binary and Count DataRadial Smoothing of Repeated Measures DataIsotonic Contrasts for Ordered AlternativesAdjusted Covariance Matrices of Fixed EffectsTesting Equality of Covariance and Correlation MatricesMultiple Trends Correspond to Multiple Extrema in Profile LikelihoodsMaximum Likelihood in Proportional Odds Model with Random EffectsFitting a Marginal (GEE-Type) ModelResponse Surface Comparisons with Multiplicity AdjustmentsGeneralized Poisson Mixed Model for Overdispersed Count DataComparing Multiple B-SplinesDiallel Experiment with Multimember Random EffectsLinear Inference Based on Summary DataWeighted Multilevel Model for Survey DataQuadrature Method for Multilevel Model - References
Comparing the GLIMMIX and MIXED Procedures
The MIXED procedure is subsumed by the GLIMMIX procedure in the following sense:
-
Linear mixed models are a special case in the family of generalized linear mixed models; a linear mixed model is a generalized linear mixed model where the conditional distribution is normal and the link function is the identity function.
-
Most models that can be fit with the MIXED procedure can also be fit with the GLIMMIX procedure.
Despite this overlap in functionality, there are also some important differences between the two procedures. Awareness of these differences enables you to select the most appropriate tool in situations where you have a choice between procedures and to identify situations where a choice does not exist. Furthermore, the %GLIMMIX macro, which fits generalized linear mixed models by linearization methods, essentially calls the MIXED procedure repeatedly. If you are aware of the syntax differences between the procedures, you can easily convert your %GLIMMIX macro statements.
Important functional differences between PROC GLIMMIX and PROC MIXED for linear models and linear mixed models include the following:
-
The MIXED procedure models R-side effects through the REPEATED statement and G-side effects through the RANDOM statement. The GLIMMIX procedure models all random components of the model through the RANDOM statement. You use the _RESIDUAL_ keyword or the RESIDUAL option in the RANDOM statement to model R-side covariance structure in the GLIMMIX procedure. For example, the PROC MIXED statement
repeated / subject=id type=ar(1);
is equivalent to the following RANDOM statement in the GLIMMIX procedure:
random _residual_ / subject=id type=ar(1);
If you need to specify an effect for levelization—for example, because the construction of the
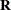 matrix is order-dependent or because you need to account for missing values—the RESIDUAL
option in the RANDOM
statement of the GLIMMIX procedure is used to indicate that you are modeling an R-side covariance nature. For example, the
PROC MIXED statements
matrix is order-dependent or because you need to account for missing values—the RESIDUAL
option in the RANDOM
statement of the GLIMMIX procedure is used to indicate that you are modeling an R-side covariance nature. For example, the
PROC MIXED statements
class time id; repeated time / subject=id type=ar(1);
are equivalent to the following PROC GLIMMIX statements:
class time id; random time / subject=id type=ar(1) residual;
-
There is generally considerable overlap in the covariance structures available through the TYPE= option in the RANDOM statement in PROC GLIMMIX and through the TYPE= options in the RANDOM and REPEATED statements in PROC MIXED. However, the Kronecker-type structures, the geometrically anisotropic spatial structures, and the GDATA= option in the RANDOM statement of the MIXED procedure are currently not supported in the GLIMMIX procedure. The MIXED procedure, on the other hand, does not support TYPE= RSMOOTH and TYPE= PSPLINE .
-
For normal linear mixed models, the (default) METHOD= RSPL in PROC GLIMMIX is identical to the default METHOD=REML in PROC MIXED. Similarly, METHOD= MSPL in PROC GLIMMIX is identical for these models to METHOD=ML in PROC MIXED. The GLIMMIX procedure does not support Type I through Type III (ANOVA) estimation methods for variance component models. Also, the procedure does not have a METHOD=MIVQUE0 option, but you can produce these estimates through the NOITER option in the PARMS statement.
-
The MIXED procedure solves the iterative optimization problem by means of a ridge-stabilized Newton-Raphson algorithm. With the GLIMMIX procedure, you can choose from a variety of optimization methods via the NLOPTIONS statement. The default method for most GLMMs is a quasi-Newton algorithm. A ridge-stabilized Newton-Raphson algorithm, akin to the optimization method in the MIXED procedure, is available in the GLIMMIX procedure through the TECHNIQUE=NRRIDG option in the NLOPTIONS statement. Because of differences in the line-search methods, update methods, and the convergence criteria, you might get slightly different estimates with the two procedures in some instances. The GLIMMIX procedure, for example, monitors several convergence criteria simultaneously.
-
You can produce predicted values, residuals, and confidence limits for predicted values with both procedures. The mechanics are slightly different, however. With the MIXED procedure you use the OUTPM= and OUTP= options in the MODEL statement to write statistics to data sets. With the GLIMMIX procedure you use the OUTPUT statement and indicate with keywords which "flavor" of a statistic to compute.
-
The following GLIMMIX statements are not available in the MIXED procedure: COVTEST , EFFECT , FREQ , LSMESTIMATE , OUTPUT , and programming statements .
-
A sampling-based Bayesian analysis as through the PRIOR statement in the MIXED procedure is not available in the GLIMMIX procedure.
-
In the GLIMMIX procedure, several RANDOM statement options apply to the RANDOM statement in which they are specified. For example, the following statements in the GLIMMIX procedure request that the solution vector be printed for the
AandA*B*Crandom effects and that the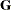 matrix corresponding to the
matrix corresponding to the A*Binteraction random effect be displayed:random a / s; random a*b / G; random a*b*c / alpha=0.04;
Confidence intervals with a 0.96 coverage probability are produced for the solutions of the
A*B*Ceffect. In the MIXED procedure, the S option, for example, when specified in one RANDOM statement, applies to all RANDOM statements. -
If you select nonmissing values in the value-list of the DDF= option in the MODEL statement, PROC GLIMMIX uses these values to override degrees of freedom for this effect that might be determined otherwise. For example, the following statements request that the denominator degrees of freedom for tests and confidence intervals involving the
Aeffect be set to 4:proc glimmix; class block a b; model y = a b a*b / s ddf=4,.,. ddfm=satterthwaite; random block a*block / s; lsmeans a b a*b / diff; run;
In the example, this applies to the "Type III Tests of Fixed Effects," "Least Squares Means," and "Differences of Least Squares Means" tables. In the MIXED procedure, the Satterthwaite approximation overrides the DDF= specification.
-
The DDFM= BETWITHIN degrees-of-freedom method in the GLIMMIX procedure requires that the data be processed by subjects; see the section Processing by Subjects.
-
When you add the response variable to the CLASS statement, PROC GLIMMIX defaults to the multinomial distribution. Adding the response variable to the CLASS statement in PROC MIXED has no effect on the fitted model.
-
The ODS name of the table for the solution of fixed effects is SolutionF in the MIXED procedure. In PROC GLIMMIX, the name of the table that contains fixed-effects solutions is ParameterEstimates. In generalized linear models, this table also contains scale parameters and overdispersion parameters. The MIXED procedure always produces a "Covariance Parameter Estimates" table. The GLIMMIX procedure produces this table only in mixed models or models with nontrivial R-side covariance structure.
-
If you compute predicted values in the GLIMMIX procedure in a model with only R-side random components and missing values for the dependent variable, the predicted values will not be kriging predictions as is the case with the MIXED procedure.