The GLIMMIX Procedure
-
Overview
-
Getting Started
-
SyntaxPROC GLIMMIX StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementCOVTEST StatementEFFECT StatementESTIMATE StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPARMS StatementRANDOM StatementSLICE StatementSTORE StatementWEIGHT StatementProgramming StatementsUser-Defined Link or Variance Function
-
DetailsGeneralized Linear Models TheoryGeneralized Linear Mixed Models TheoryGLM Mode or GLMM ModeStatistical Inference for Covariance ParametersDegrees of Freedom MethodsEmpirical Covariance ("Sandwich") EstimatorsExploring and Comparing Covariance MatricesProcessing by SubjectsRadial Smoothing Based on Mixed ModelsOdds and Odds Ratio EstimationParameterization of Generalized Linear Mixed ModelsResponse-Level Ordering and ReferencingComparing the GLIMMIX and MIXED ProceduresSingly or Doubly Iterative FittingDefault Estimation TechniquesDefault OutputNotes on Output StatisticsODS Table NamesODS Graphics
-
ExamplesBinomial Counts in Randomized BlocksMating Experiment with Crossed Random EffectsSmoothing Disease Rates; Standardized Mortality RatiosQuasi-likelihood Estimation for Proportions with Unknown DistributionJoint Modeling of Binary and Count DataRadial Smoothing of Repeated Measures DataIsotonic Contrasts for Ordered AlternativesAdjusted Covariance Matrices of Fixed EffectsTesting Equality of Covariance and Correlation MatricesMultiple Trends Correspond to Multiple Extrema in Profile LikelihoodsMaximum Likelihood in Proportional Odds Model with Random EffectsFitting a Marginal (GEE-Type) ModelResponse Surface Comparisons with Multiplicity AdjustmentsGeneralized Poisson Mixed Model for Overdispersed Count DataComparing Multiple B-SplinesDiallel Experiment with Multimember Random EffectsLinear Inference Based on Summary DataWeighted Multilevel Model for Survey DataQuadrature Method for Multilevel Model
- References
Implications of the Non-Full-Rank Parameterization
For models with fixed effects involving classification variables, there are more design columns in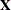 
constructed than there are degrees of freedom for the effect. Thus, there are linear dependencies among the columns of 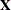. In this event, all of the parameters are not estimable; there is an infinite number of solutions to the mixed model equations.
The GLIMMIX procedure uses a generalized inverse (a 
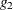-inverse, Pringle and Rayner (1971), to obtain values for the estimates (Searle 1971). The solution values are not displayed unless you specify the SOLUTION
option in the MODEL
statement. The solution has the characteristic that estimates are 0 whenever the design column for that parameter is a linear
combination of previous columns. With this parameterization, hypothesis tests are constructed to test linear functions of
the parameters that are estimable.
Some procedures (such as the CATMOD and LOGISTIC procedures) reparameterize models to full rank by using restrictions on the parameters. PROC GLM, PROC MIXED, and PROC GLIMMIX do not reparameterize, making the hypotheses that are commonly tested more understandable. See Goodnight (1978b) for additional reasons for not reparameterizing.