The GLIMMIX Procedure

From Penalized Splines to Mixed Models

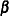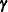The connection between splines and mixed models arises from the similarity of the penalized spline fitting criterion to the minimization problem that yields the mixed model equations and solutions for $\bbeta $ and $\bgamma $. This connection is made explicit in the following paragraphs. An important distinction between classical spline fitting and its mixed model smoothing variant, however, lies in the nature of the spline coefficients. Although they address similar minimization criteria, the solutions for the spline coefficients in the GLIMMIX procedure are the solutions of random effects, not fixed effects. Standard errors of predicted values, for example, account for this source of variation.

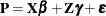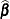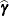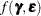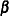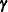Consider the linearized mixed pseudo-model from the section The Pseudo-model, $\bP = \bX \bbeta + \bZ \bgamma + \bepsilon $. One derivation of the mixed model equations, whose solutions are $\widehat{\bbeta }$ and $\widehat{\bgamma }$, is to maximize the joint density of $f(\bgamma ,\bepsilon )$ with respect to $\bbeta $ and $\bgamma $. This is not a true likelihood problem, because 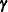$\bgamma $ is not a parameter, but a random vector.

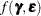In the special case with $\mr{Var}[\bepsilon ] = \phi \bI $ and $\mr{Var}[\bgamma ] = \sigma ^2 \bI $, the maximization of $f(\bgamma ,\bepsilon )$ is equivalent to the minimization of

\[ Q(\bbeta ,\bgamma ) = \phi ^{-1}(\mb{p} - \bX \bbeta - \bZ \bgamma )’ (\mb{p} - \bX \bbeta - \bZ \bgamma ) + \sigma ^{-2} \bgamma ’\bgamma \]

Now consider a linear spline as in Ruppert, Wand, and Carroll (2003, p. 108),

\[ p_ i = \beta _0 + \beta _1 x_ i + \sum _{j=1}^{K} \gamma _ j (x_ i - t_ j)_+ \]

where the 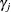$\gamma _ j$ denote the spline coefficients at knots 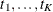$t_1, \ldots , t_ K$. The truncated line function is defined as

\[ (x - t)_+ = \left\{ \begin{array}{ll} x - t & \quad x > t \\ 0 & \quad \mr{ otherwise} \end{array} \right. \]

If you collect the intercept and regressor x into the matrix 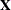$\mb{X}$, and if you collect the truncated line functions into the 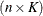$(n \times K)$ matrix 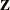$\mb{Z}$, then fitting the linear spline amounts to minimization of the penalized spline criterion

\[ Q^*(\bbeta ,\bgamma ) = (\mb{p} - \mb{X}\bbeta - \mb{Z}\bgamma )’ (\mb{p} - \mb{X}\bbeta - \mb{Z}\bgamma ) + \lambda ^2 \bgamma ’\bgamma \]

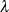where $\lambda $ is the smoothing parameter.

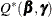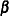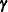Because minimizing $Q^*(\bbeta ,\bgamma )$ with respect to $\bbeta $ and $\bgamma $ is equivalent to minimizing 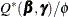$Q^*(\bbeta ,\bgamma )/\phi $, both problems lead to the same solution, and 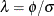$\lambda =\phi /\sigma $ is the smoothing parameter. The mixed model formulation of spline smoothing has the advantage that the smoothing parameter is selected "automatically." It is a function of the covariance parameter estimates, which, in turn, are estimated according to the method you specify with the METHOD= option in the PROC GLIMMIX statement.

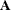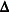To accommodate nonnormal responses and general link functions, the GLIMMIX procedure uses $\mr{Var}[\bepsilon ] = \phi \widetilde{\bDelta }^{-1}\mb{A}\widetilde{\bDelta }^{-1}$, where $\mb{A}$ is the matrix of variance functions and $\bDelta $ is the diagonal matrix of mean derivatives defined earlier. The correspondence between spline smoothing and mixed modeling is then one between a weighted linear mixed model and a weighted spline. 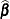In other words, the minimization criterion that yields the estimates $\widehat{\bbeta }$ and solutions 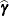$\widehat{\bgamma }$ is then

\[ Q(\bbeta ,\bgamma ) = \phi ^{-1} (\mb{p} - \mb{X}\bbeta - \mb{Z}\bgamma )’ \widetilde{\bDelta }\mb{A}^{-1}\widetilde{\bDelta } (\mb{p} - \mb{X}\bbeta - \mb{Z}\bgamma )’ + \sigma ^{-2}\bgamma ’\bgamma \]

If you choose the TYPE=RSMOOTH covariance structure, PROC GLIMMIX chooses radial basis functions as the spline basis and transforms them to approximate a thin-plate spline as in Chapter 13.4 of Ruppert, Wand, and Carroll (2003). For computational expediency, the number of knots is chosen to be less than the number of data points. Ruppert, Wand, and Carroll (2003) recommend one knot per every four unique regressor values for one-dimensional smoothers. In the multivariate case, general recommendations are more difficult, because the optimal number and placement of knots depend on the spatial configuration of samples. Their recommendation for a bivariate smoother is one knot per four samples, but at least 20 and no more than 150 knots (Ruppert, Wand, and Carroll 2003, p. 257).

The magnitude of the variance component 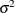$\sigma ^2$ depends on the metric of the random effects. For example, if you apply radial smoothing in time, the variance changes if you measure time in days or minutes. If the solution for the variance component is near zero, then a rescaling of the random effect data can help the optimization problem by moving the solution for the variance component away from the boundary of the parameter space.