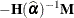The GLIMMIX Procedure
-
Overview

-
Getting Started

-
Syntax
 PROC GLIMMIX StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementCOVTEST StatementEFFECT StatementESTIMATE StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPARMS StatementRANDOM StatementSLICE StatementSTORE StatementWEIGHT StatementProgramming StatementsUser-Defined Link or Variance Function
PROC GLIMMIX StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementCOVTEST StatementEFFECT StatementESTIMATE StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPARMS StatementRANDOM StatementSLICE StatementSTORE StatementWEIGHT StatementProgramming StatementsUser-Defined Link or Variance Function -
Details
 Generalized Linear Models TheoryGeneralized Linear Mixed Models TheoryGLM Mode or GLMM ModeStatistical Inference for Covariance ParametersDegrees of Freedom MethodsEmpirical Covariance ("Sandwich") EstimatorsExploring and Comparing Covariance MatricesProcessing by SubjectsRadial Smoothing Based on Mixed ModelsOdds and Odds Ratio EstimationParameterization of Generalized Linear Mixed ModelsResponse-Level Ordering and ReferencingComparing the GLIMMIX and MIXED ProceduresSingly or Doubly Iterative FittingDefault Estimation TechniquesDefault OutputNotes on Output StatisticsODS Table NamesODS Graphics
Generalized Linear Models TheoryGeneralized Linear Mixed Models TheoryGLM Mode or GLMM ModeStatistical Inference for Covariance ParametersDegrees of Freedom MethodsEmpirical Covariance ("Sandwich") EstimatorsExploring and Comparing Covariance MatricesProcessing by SubjectsRadial Smoothing Based on Mixed ModelsOdds and Odds Ratio EstimationParameterization of Generalized Linear Mixed ModelsResponse-Level Ordering and ReferencingComparing the GLIMMIX and MIXED ProceduresSingly or Doubly Iterative FittingDefault Estimation TechniquesDefault OutputNotes on Output StatisticsODS Table NamesODS Graphics -
Examples
 Binomial Counts in Randomized BlocksMating Experiment with Crossed Random EffectsSmoothing Disease Rates; Standardized Mortality RatiosQuasi-likelihood Estimation for Proportions with Unknown DistributionJoint Modeling of Binary and Count DataRadial Smoothing of Repeated Measures DataIsotonic Contrasts for Ordered AlternativesAdjusted Covariance Matrices of Fixed EffectsTesting Equality of Covariance and Correlation MatricesMultiple Trends Correspond to Multiple Extrema in Profile LikelihoodsMaximum Likelihood in Proportional Odds Model with Random EffectsFitting a Marginal (GEE-Type) ModelResponse Surface Comparisons with Multiplicity AdjustmentsGeneralized Poisson Mixed Model for Overdispersed Count DataComparing Multiple B-SplinesDiallel Experiment with Multimember Random EffectsLinear Inference Based on Summary DataWeighted Multilevel Model for Survey DataQuadrature Method for Multilevel Model
Binomial Counts in Randomized BlocksMating Experiment with Crossed Random EffectsSmoothing Disease Rates; Standardized Mortality RatiosQuasi-likelihood Estimation for Proportions with Unknown DistributionJoint Modeling of Binary and Count DataRadial Smoothing of Repeated Measures DataIsotonic Contrasts for Ordered AlternativesAdjusted Covariance Matrices of Fixed EffectsTesting Equality of Covariance and Correlation MatricesMultiple Trends Correspond to Multiple Extrema in Profile LikelihoodsMaximum Likelihood in Proportional Odds Model with Random EffectsFitting a Marginal (GEE-Type) ModelResponse Surface Comparisons with Multiplicity AdjustmentsGeneralized Poisson Mixed Model for Overdispersed Count DataComparing Multiple B-SplinesDiallel Experiment with Multimember Random EffectsLinear Inference Based on Summary DataWeighted Multilevel Model for Survey DataQuadrature Method for Multilevel Model - References
Design-Adjusted MBN Estimator
Morel (1989) and Morel, Bokossa, and Neerchal (2003) suggested a bias correction of the classical sandwich estimator that rests on an additive correction of the residual crossproducts and a sample size correction. This estimator is available with the EMPIRICAL= MBN option in the PROC GLIMMIX statement. In the notation of the previous section, the residual-based MBN estimator can be written as
![\[ \widehat{\bOmega } \left( \sum _{i=1}^ m \widehat{\mb{D}}_ i’ \widehat{\bSigma }_ i^{-1} \left(c \mb{e}_ i\mb{e}_ i’ + \mb{B}_ i\right) \widehat{\bSigma }_ i^{-1} \widehat{\mb{D}}_ i \right) \widehat{\bOmega } \]](images/statug_glimmix0813.png)
where
-
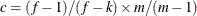 or c = 1 when you specify the EMPIRICAL=
MBN(NODF) option
or c = 1 when you specify the EMPIRICAL=
MBN(NODF) option
-
f is the sum of the frequencies
-
k equals the rank of
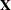
-
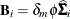
-
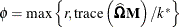
-
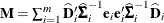
-
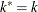 if
if 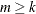 , otherwise
, otherwise 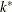 equals the number of nonzero singular values of
equals the number of nonzero singular values of 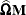
-
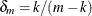 if
if 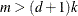 and
and 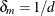 otherwise
otherwise
-
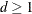 and
and 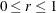 are parameters supplied with the mbn-options of the EMPIRICAL=
MBN(mbn-options) option. The default values are d = 2 and r = 1. When the NODF option is in effect, the factor c is set to 1.
are parameters supplied with the mbn-options of the EMPIRICAL=
MBN(mbn-options) option. The default values are d = 2 and r = 1. When the NODF option is in effect, the factor c is set to 1.
Rearranging terms, the MBN estimator can also be written as an additive adjustment to a sample-size corrected classical sandwich estimator
![\[ c \times \widehat{\bOmega } \left( \sum _{i=1}^ m \widehat{\mb{D}}_ i’ \widehat{\bSigma }_ i^{-1} \mb{e}_ i\mb{e}_ i’ \widehat{\bSigma }_ i^{-1} \widehat{\mb{D}}_ i \right) \widehat{\bOmega } + \delta _ m\phi \widehat{\bOmega } \]](images/statug_glimmix0825.png)
Because 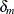 is of order
is of order 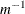 , the additive adjustment to the classical estimator vanishes as the number of independent sampling units (subjects) increases.
The parameter
, the additive adjustment to the classical estimator vanishes as the number of independent sampling units (subjects) increases.
The parameter  is a measure of the design effect (Morel, Bokossa, and Neerchal 2003). Besides good statistical properties in terms of Type I error rates in small-m situations, the MBN estimator also has the desirable property of recovering rank when the number of sampling units is small.
If
is a measure of the design effect (Morel, Bokossa, and Neerchal 2003). Besides good statistical properties in terms of Type I error rates in small-m situations, the MBN estimator also has the desirable property of recovering rank when the number of sampling units is small.
If 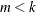 , the "meat" piece of the classical sandwich estimator is essentially a sum of rank one matrices. A small number of subjects
relative to the rank of
, the "meat" piece of the classical sandwich estimator is essentially a sum of rank one matrices. A small number of subjects
relative to the rank of 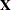 can result in a loss of rank and subsequent loss of numerator degrees of freedom in tests. The additive MBN adjustment counters
the rank exhaustion. You can examine the rank of an adjusted covariance matrix with the COVB(DETAILS)
option in the MODEL
statement.
can result in a loss of rank and subsequent loss of numerator degrees of freedom in tests. The additive MBN adjustment counters
the rank exhaustion. You can examine the rank of an adjusted covariance matrix with the COVB(DETAILS)
option in the MODEL
statement.
When the principle of the MBN estimator is applied to the likelihood-based empirical estimator, you obtain
![\[ \mb{H}(\widehat{\balpha })^{-1} \left( \sum _{i=1}^{m} c \mb{g}_ i(\widehat{\balpha }) \mb{g}_ i(\widehat{\balpha })’ + \mb{B}_ i \right) \mb{H}(\widehat{\balpha })^{-1} \]](images/statug_glimmix0829.png)
where 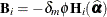 , and
, and 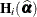 is the second derivative of the log likelihood for the ith sampling unit (subject) evaluated at the vector of parameter estimates,
is the second derivative of the log likelihood for the ith sampling unit (subject) evaluated at the vector of parameter estimates, 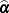 . Also,
. Also, 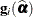 is the first derivative of the log likelihood for the ith sampling unit. This estimator is computed if you request EMPIRICAL
=MBN with METHOD=
LAPLACE
or METHOD=
QUAD
.
is the first derivative of the log likelihood for the ith sampling unit. This estimator is computed if you request EMPIRICAL
=MBN with METHOD=
LAPLACE
or METHOD=
QUAD
.
In terms of adjusting the classical likelihood-based estimator (White 1982), the likelihood MBN estimator can be written as
![\[ c \times \mb{H}(\widehat{\balpha })^{-1} \left( \sum _{i=1}^{m} \mb{g}_ i(\widehat{\balpha }) \mb{g}_ i(\widehat{\balpha })’ \right) \mb{H}(\widehat{\balpha })^{-1} - \delta _ m\phi \mb{H}(\widehat{\balpha })^{-1} \]](images/statug_glimmix0833.png)
The parameter  is determined as
is determined as
-
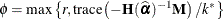
-
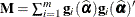
-
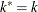 if
if 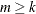 , otherwise
, otherwise 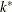 equals the number of nonzero singular values of
equals the number of nonzero singular values of