The OPTGRAPH Procedure

Consider the following road network between a SAS employee’s home in Raleigh, NC, and the SAS headquarters in Cary, NC.

In this road network (graph), the links are the roads and the nodes are intersections between roads. For each road, you assign a link attribute in the variable time_to_travel to describe the number of minutes that it takes to drive from one node to another. The following data were collected using Google Maps (Google 2011), which gives an approximate number of minutes to traverse between two points, based on the length of the road and the typical speed during normal traffic patterns:

data LinkSetInRoadNC10am;
   input start_inter $1-20 end_inter $20-40 miles miles_per_hour;
   datalines;
614CapitalBlvd      Capital/WadeAve      0.6  25
614CapitalBlvd      Capital/US70W        0.6  25
614CapitalBlvd      Capital/US440W       3.0  45
Capital/WadeAve     WadeAve/RaleighExpy  3.0  40
Capital/US70W       US70W/US440W         3.2  60
US70W/US440W        US440W/RaleighExpy   2.7  60
Capital/US440W      US440W/RaleighExpy   6.7  60
US440W/RaleighExpy  RaleighExpy/US40W    3.0  60
WadeAve/RaleighExpy RaleighExpy/US40W    3.0  60
RaleighExpy/US40W   US40W/HarrisonAve    1.3  55
US40W/HarrisonAve   SASCampusDrive       0.5  25
;

data LinkSetInRoadNC10am;
   set LinkSetInRoadNC10am;
   time_to_travel = miles * 1/miles_per_hour * 60;
run;

Using PROC OPTGRAPH, you want to find the route that yields the shortest path between home (614 Capital Blvd) and the SAS headquarters (SAS Campus Drive). This can be done with the SHORTPATH statement as follows:

proc optgraph
   data_links   = LinkSetInRoadNC10am;
   data_links_var
      from      = start_inter
      to        = end_inter
      weight    = time_to_travel;
   shortpath
      out_paths = ShortPath
      source    = "614CapitalBlvd"
      sink      = "SASCampusDrive";
run;

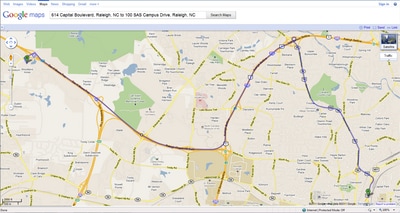
For more information about shortest path algorithms in PROC OPTGRAPH, see the section Shortest Path. Figure 1.2 displays the output data set ShortPath, which shows the best route to take to minimize travel time at 10:00 a.m. This route is also shown in Google Maps in Figure 1.3.

Figure 1.3: Shortest Path for Road Network at 10:00 A.M. in Google Maps

Now suppose that it is rush hour (5:00 p.m.) and the time to traverse the roads has changed because of traffic patterns. You want to find the route that is the shortest path for going home from SAS headquarters under different speed assumptions due to traffic. The following data set lists approximate travel times and speeds for driving in the opposite direction:

data LinkSetInRoadNC5pm;
   input start_inter $1-20 end_inter $20-40 miles miles_per_hour;
   datalines;
614CapitalBlvd      Capital/WadeAve      0.6  25
614CapitalBlvd      Capital/US70W        0.6  25
614CapitalBlvd      Capital/US440W       3.0  45
Capital/WadeAve     WadeAve/RaleighExpy  3.0  25 /*high traffic*/
Capital/US70W       US70W/US440W         3.2  60
US70W/US440W        US440W/RaleighExpy   2.7  60
Capital/US440W      US440W/RaleighExpy   6.7  60
US440W/RaleighExpy  RaleighExpy/US40W    3.0  60
WadeAve/RaleighExpy RaleighExpy/US40W    3.0  60
RaleighExpy/US40W   US40W/HarrisonAve    1.3  55
US40W/HarrisonAve   SASCampusDrive       0.5  25
;

data LinkSetInRoadNC5pm;
   set LinkSetInRoadNC5pm;
   time_to_travel = miles * 1/miles_per_hour * 60;
run;

The following statements are similar to the first PROC OPTGRAPH run, except that they use the data set LinkSetInRoadNC5pm and the SOURCE and SINK option values are reversed:

proc optgraph
   data_links   = LinkSetInRoadNC5pm;
   data_links_var
      from      = start_inter
      to        = end_inter
      weight    = time_to_travel;
   shortpath
      out_paths = ShortPath
      source    = "SASCampusDrive"
      sink      = "614CapitalBlvd";
run;

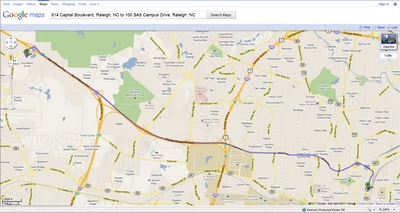
Now, the output data set ShortPath, shown in Figure 1.4, shows the best route for going home. Because the traffic on Wade Avenue is usually heavy at this time of day, the route home is different from the route to work.

This new route is shown in Google Maps in Figure 1.5.

Figure 1.5: Shortest Path for Road Network at 5:00 P.M. in Google Maps