The OPTGRAPH Procedure
- Overview
-
Getting Started

-
Syntax
 Functional SummaryPROC OPTGRAPH StatementBICONCOMP StatementCENTRALITY StatementCLIQUE StatementCOMMUNITY StatementCONCOMP StatementCORE StatementCYCLE StatementDATA_LINKS_VAR StatementDATA_MATRIX_VAR StatementDATA_NODES_VAR StatementEIGENVECTOR StatementLINEAR_ASSIGNMENT StatementMINCOSTFLOW StatementMINCUT StatementMINSPANTREE StatementPERFORMANCE StatementREACH StatementSHORTPATH StatementSUMMARY StatementTRANSITIVE_CLOSURE StatementTSP Statement
Functional SummaryPROC OPTGRAPH StatementBICONCOMP StatementCENTRALITY StatementCLIQUE StatementCOMMUNITY StatementCONCOMP StatementCORE StatementCYCLE StatementDATA_LINKS_VAR StatementDATA_MATRIX_VAR StatementDATA_NODES_VAR StatementEIGENVECTOR StatementLINEAR_ASSIGNMENT StatementMINCOSTFLOW StatementMINCUT StatementMINSPANTREE StatementPERFORMANCE StatementREACH StatementSHORTPATH StatementSUMMARY StatementTRANSITIVE_CLOSURE StatementTSP Statement -
Details
 Graph Input DataMatrix Input DataData Input OrderParallel ProcessingNumeric LimitationsSize LimitationsCommon Notation and AssumptionsBiconnected Components and Articulation PointsCentralityCliqueCommunityConnected ComponentsCore DecompositionCycleEigenvector ProblemLinear Assignment (Matching)Minimum-Cost Network FlowMinimum CutMinimum Spanning TreeReach (Ego) NetworkShortest PathSummaryTransitive ClosureTraveling Salesman ProblemMacro VariablesODS Table Names
Graph Input DataMatrix Input DataData Input OrderParallel ProcessingNumeric LimitationsSize LimitationsCommon Notation and AssumptionsBiconnected Components and Articulation PointsCentralityCliqueCommunityConnected ComponentsCore DecompositionCycleEigenvector ProblemLinear Assignment (Matching)Minimum-Cost Network FlowMinimum CutMinimum Spanning TreeReach (Ego) NetworkShortest PathSummaryTransitive ClosureTraveling Salesman ProblemMacro VariablesODS Table Names -
Examples
 Articulation Points in a Terrorist NetworkInfluence Centrality for Project Groups in a Research DepartmentBetweenness and Closeness Centrality for Computer Network TopologyBetweenness and Closeness Centrality for Project Groups in a Research DepartmentEigenvector Centrality for Word Sense DisambiguationCentrality Metrics for Project Groups in a Research DepartmentCommunity Detection on Zachary’s Karate Club DataRecursive Community Detection on Zachary’s Karate Club DataCycle Detection for Kidney Donor ExchangeLinear Assignment Problem for Minimizing Swim TimesLinear Assignment Problem, Sparse Format versus Dense FormatMinimum Spanning Tree for Computer Network TopologyTransitive Closure for Identification of Circular Dependencies in a Bug Tracking SystemReach Networks for Computation of Market Coverage of a Terrorist NetworkTraveling Salesman Tour through US Capital Cities
Articulation Points in a Terrorist NetworkInfluence Centrality for Project Groups in a Research DepartmentBetweenness and Closeness Centrality for Computer Network TopologyBetweenness and Closeness Centrality for Project Groups in a Research DepartmentEigenvector Centrality for Word Sense DisambiguationCentrality Metrics for Project Groups in a Research DepartmentCommunity Detection on Zachary’s Karate Club DataRecursive Community Detection on Zachary’s Karate Club DataCycle Detection for Kidney Donor ExchangeLinear Assignment Problem for Minimizing Swim TimesLinear Assignment Problem, Sparse Format versus Dense FormatMinimum Spanning Tree for Computer Network TopologyTransitive Closure for Identification of Circular Dependencies in a Bug Tracking SystemReach Networks for Computation of Market Coverage of a Terrorist NetworkTraveling Salesman Tour through US Capital Cities - References
Reach (Ego) Network
The reach network of a graph ![]() is a graph
is a graph ![]() that is defined as the induced subgraph over the set of nodes
that is defined as the induced subgraph over the set of nodes ![]() that are reachable in L steps (or hops) from a set S of nodes, called the source nodes. Reach networks are often referred to as ego networks in the context of social networks, since they focus around the neighbors of one (or more) particular individuals.
that are reachable in L steps (or hops) from a set S of nodes, called the source nodes. Reach networks are often referred to as ego networks in the context of social networks, since they focus around the neighbors of one (or more) particular individuals.
In PROC OPTGRAPH, reach networks can be calculated by using the REACH statement. The options for this statement are described in the section REACH Statement.
The REACH statement reports status information in a macro variable called _OPTGRAPH_REACH_. See the section Macro Variable _OPTGRAPH_REACH_ for more information about this macro variable.
In most cases, the set of source nodes from which to calculate reach are defined in a node subset data set, as described in
the section Node Subset Input Data. The node subset data set can be used to define several sets of sources nodes. Each source node set is used to calculate
the reach networks. The reach network identifier is given in the node subset data set’s reach column. When you use the EACH_SOURCE option, every node in the original graph’s node set N is used to find a reach network from each node separately.
Output Data Sets
Depending on the options selected, the reach network algorithm produces output data sets as described in the following sections.
OUT_NODES= Data Set
This data set describes the nodes in each reach network that are found from each set of source nodes. The data set contains the following columns:
-
node: node label for each node in each reach network -
reach: reach network identifier (which defines the set of source nodes that was used)
OUT_LINKS= Data Set
This data set describes the links in each reach network that are found from each set of source nodes. Output of the reach network links can sometimes be more costly computationally, relative to calculating only the nodes or counts in the reach networks. This option does not work when you use the BY_CLUSTER option. The data set contains the following columns:
-
from: the from node label for each link in each reach network -
to: the to node label for each link in each reach network -
reach: reach network identifier (which defines the set of source nodes that was used)
OUT_COUNTS= Data Set
This data set describes the number of nodes in each reach network for each set of sources nodes. The data set contains the following columns:
-
node: node label for each node in the source node sets -
reach: reach network identifier (which defines the set of source nodes that was used) -
count: the number of nodes reachable using outgoing links from the source nodes -
count_not: the number of nodes not reachable using outgoing links from the source nodes
If the graph is directed and you use the DIGRAPH option, then the OUT_COUNTS= data set contains the following additional columns:
-
count_in: the number of nodes reachable using incoming links from the source node -
count_out: the number of nodes reachable using outgoing links from the source node (equivalent tocount) -
count_in_or_out: the number of nodes reachable using incoming or outgoing links (but not both) from the source node -
count_in_and_out: the number of nodes reachable using both incoming and outgoing links from the source node
If node weights are present, the OUT_COUNTS= data set contains the following additional columns:
-
count_wt: the sum of the weights of the nodes reachable using outgoing links from the source node -
count_not_wt: the sum of the weights of the nodes not reachable from the source node -
count_in_wt: the sum of the weights of the nodes reachable using incoming links from the source node -
count_out_wt: the sum of the weights of the nodes reachable using outgoing links from the source node -
count_in_or_out_wt: the sum of the weights of the nodes reachable using incoming or outgoing links (but not both) from the source node -
count_in_and_out_wt: the sum of the weights of the nodes reachable using both incoming and outgoing links from the source node
When you want to calculate hop limits of 1 and 2 on the same graph, you can use the OUT_COUNTS1= and OUT_COUNTS2= options to do this in one call. This option works only when the EACH_SOURCE and BY_CLUSTER options are specified.
Reach Network of a Simple Directed Graph
This section illustrates the use of the reach networks algorithm on the simple directed graph G that is shown in Figure 1.91.
Figure 1.91: Simple Directed Graph G
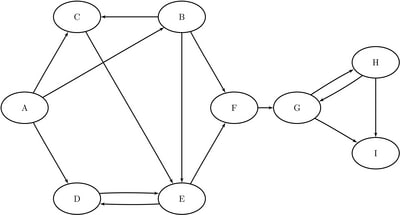
The directed graph G can be represented using the following links data set LinkSetIn:
data LinkSetIn; input from $ to $ @@; datalines; A B A C A D B C B E B F C E D E E D E F F G G H G I H G H I ;
Consider two sets of source nodes, ![]() and
and ![]() . These can be defined separately in two node subset data sets as follows:
. These can be defined separately in two node subset data sets as follows:
data NodeSubSetIn1; input node $ reach; datalines; A 1 G 1 ; data NodeSubSetIn2; input node $ reach; datalines; B 1 ;
For the first set of source nodes, you can use the following statements to calculate the reach network with a hop limit of 1:
proc optgraph
graph_direction = directed
data_links = LinkSetIn
data_nodes_sub = NodeSubSetIn1;
reach
out_nodes = ReachNodes1
out_links = ReachLinks1
out_counts = ReachCounts1
maxreach = 1;
run;
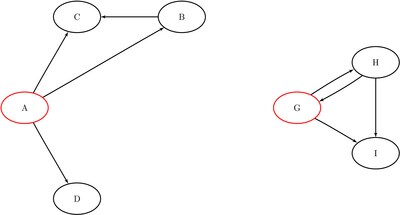
The data sets ReachNodes1, ReachLinks1, and ReachCounts1 now contain the nodes, links, and counts of the reach network, respectively, that come from ![]() .
.
Figure 1.92: Reach Network for ![]() with Hop Limit of 1
with Hop Limit of 1
The results are displayed graphically in Figure 1.93.
Figure 1.93: Reach Network for ![]() with Hop Limit of 1
with Hop Limit of 1
For the second set of source nodes, you can use the following statements to calculate the reach network with a hop limit of 2:
proc optgraph
graph_direction = directed
data_links = LinkSetIn
data_nodes_sub = NodeSubSetIn2;
reach
out_nodes = ReachNodes2
out_links = ReachLinks2
out_counts = ReachCounts2
maxreach = 2;
run;
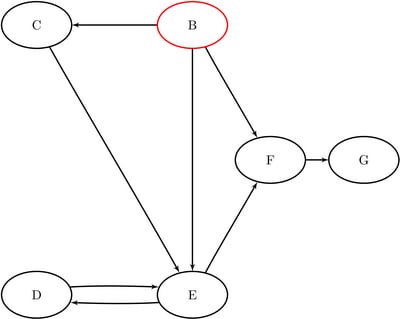
The data sets ReachNodes2, ReachLinks2, and ReachCounts2 now contain the nodes, links, and counts of the reach network, respectively, that come from ![]() .
.
Figure 1.94: Reach Network for ![]() with Hop Limit of 2
with Hop Limit of 2
The results are displayed graphically in Figure 1.95.
Figure 1.95: Reach Network for ![]() with Hop Limit of 2
with Hop Limit of 2
Processing Multiple Reach Networks in One Pass
You can process a set of reach networks from one graph in one pass using one node subset data set. The MAXREACH= option applies
to all of the reach networks requested. If the node subset data set column reach is set to 0 or missing (.), then the node is not processed. If the column reach is set to a value greater than 0, then the node is processed with other nodes by using the same marker.
Consider again the graph shown in Figure 1.91, now with source node sets ![]() and
and ![]() . These source node sets can be defined together as follows:
. These source node sets can be defined together as follows:
data NodeSubSetIn; input node $ reach; datalines; A 2 C 1 H 2 ;
You can use the following statements to process the two one-hop-limit reach networks in one pass:
proc optgraph
graph_direction = directed
data_links = LinkSetIn
data_nodes_sub = NodeSubSetIn;
reach
out_nodes = ReachNodes
out_links = ReachLinks
out_counts = ReachCounts
maxreach = 1;
run;
The data sets ReachNodes, ReachLinks, and ReachCounts now contain the nodes, links, and counts of the reach networks, respectively, that come from ![]() and
and ![]() .
.
Figure 1.96: Reach Networks for ![]() and
and ![]() with Hop Limit of 1
with Hop Limit of 1
Processing Reach Networks by Cluster
Similar to the usage for centrality described in the section Processing by Cluster, you can use the BY_CLUSTER
option in the REACH statement to process a number of induced subgraphs of a graph with only one call to PROC OPTGRAPH. In
this section, you want to work on the subgraphs that are induced by node subsets ![]() and
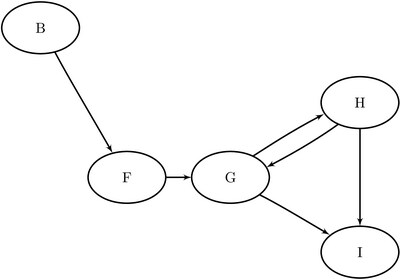
and ![]() for the directed graph shown in Figure 1.91. The induced subgraphs are shown graphically in Figure 1.97 and Figure 1.98.
for the directed graph shown in Figure 1.91. The induced subgraphs are shown graphically in Figure 1.97 and Figure 1.98.
Figure 1.97: Induced Subgraph for ![]()
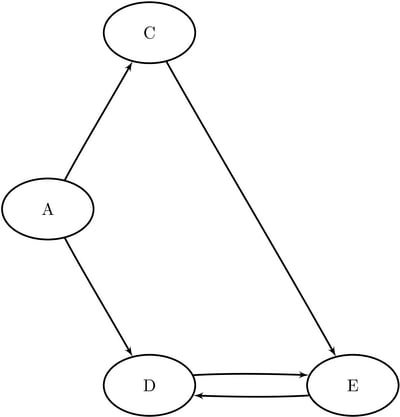
Figure 1.98: Induced Subgraph for ![]()
Define the subgraphs in the nodes data set by using the cluster variable as follows:
data NodeSetIn; input node $ cluster @@; datalines; A 0 B 1 C 0 D 0 E 0 F 1 G 1 H 1 I 1 ;
In the node subset data set, define the source nodes set ![]() by using the
by using the reach variable as follows:
data NodeSubSetIn; input node $ reach; datalines; B 1 C 1 ;
To process the two-hop-limit reach network for each induced subgraph, you can use the following statements:
proc optgraph
graph_direction = directed
data_links = LinkSetIn
data_nodes = NodeSetIn
data_nodes_sub = NodeSubSetIn;
performance
nthreads = 2;
reach
by_cluster
out_nodes = ReachNodes
out_counts = ReachCounts
maxreach = 2;
run;
Notice in this example that you can process each subgraph in parallel by using the NTHREADS= option in the PERFORMANCE statement.
The data sets ReachNodes and ReachCounts now contain the nodes and counts of the reach networks, respectively, that come from S for each induced subgraph.
Figure 1.99: Reach Networks for ![]() with Hop Limit of 2 for Induced Subgraphs
with Hop Limit of 2 for Induced Subgraphs
Notice that since you are operating on the induced subgraphs (not the original graph), node B cannot reach nodes C and E because they are not in its induced subgraph.
Processing Multiple Reach Networks in One Pass by Cluster
You can also process several reach networks in one pass while looking over decomposed subgraphs. Consider the same original graph and subgraphs from the section Processing Reach Networks by Cluster. Now, suppose you want the one-hop-limit reach network where each original node is its own source node subset. Define nine source sets by using the node subset data set as follows:
data NodeSubSetIn; input node $ reach @@; datalines; A 1 B 2 C 3 D 4 E 5 F 6 G 7 H 8 I 9 ;
Then, to calculate the reach networks (including the directed graph counts) for each source node set on the induced subgraphs, use the following statements:
proc optgraph
graph_direction = directed
data_links = LinkSetIn
data_nodes = NodeSetIn
data_nodes_sub = NodeSubSetIn;
performance
nthreads = 2;
reach
by_cluster
digraph
out_nodes = ReachNodes
out_counts = ReachCounts
maxreach = 1;
run;
Notice that you can do the same thing using the EACH_SOURCE option. In this case, you do not need the subset data set.
proc optgraph
graph_direction = directed
data_links = LinkSetIn
data_nodes = NodeSetIn;
performance
nthreads = 2;
reach
each_source
by_cluster
digraph
out_nodes = ReachNodes
out_counts = ReachCounts
maxreach = 1;
run;
The resulting data sets ReachNodes and ReachCounts are displayed in Figure 1.100.
Figure 1.100: Reach Networks for Each Source for Induced Subgraphs with a Node Hop Limit of 1
Processing Each Source Reach Network for Hop Limits of Both 1 and 2 in One Pass by Cluster
In this section, suppose you want to calculate the one-hop- and two-hop-limit reach counts on the same graph for each source node on a set of induced subgraphs. You can do this in one pass by using the OUT_COUNTS1= and OUT_COUNTS2= options, as follows:
proc optgraph
graph_direction = directed
data_links = LinkSetIn
data_nodes = NodeSetIn;
performance
nthreads = 2;
reach
each_source
by_cluster
out_counts1 = ReachCounts1
out_counts2 = ReachCounts2;
run;
The resulting data sets ReachCounts1 and ReachCounts1 are displayed in Figure 1.101.
Figure 1.101: Reach Counts for Each Source Node for Induced Subgraphs with a Hop Limit of 1 and 2
For a more detailed example, see Reach Networks for Computation of Market Coverage of a Terrorist Network.