The OPTGRAPH Procedure

A clique of a graph is an induced subgraph that is a complete graph. Every node in a clique is connected to every other node in that clique. A maximal clique is a clique that is not a subset of the nodes of any larger clique. That is, it is a set C of nodes such that every pair of nodes in C is connected by a link and every node not in C is missing a link to at least one node in C. The number of maximal cliques in a particular graph can be very large and can grow exponentially with every node added. Finding cliques in graphs has applications in numerous industries including bioinformatics, social networks, electrical engineering, and chemistry.

You can find the maximal cliques of an input graph by invoking the CLIQUE statement. The options for this statement are described in the section CLIQUE Statement. The clique algorithm works only with undirected graphs.

The results for the clique algorithm are written to the output data set that is specified in the OUT= option in the CLIQUE statement. Each node of each clique is listed in the output data set along with the variable clique to identify the clique to which it belongs. A node can appear multiple times in this data set if it belongs to multiple cliques.

The clique algorithm reports status information in a macro variable called _OPTGRAPH_CLIQUE_. See the section Macro Variable _OPTGRAPH_CLIQUE_ for more information about this macro variable.

The algorithm that PROC OPTGRAPH uses to compute maximal cliques is a variant of the Bron-Kerbosch algorithm (Bron and Kerbosch 1973; Harley 2003). Enumerating all maximal cliques is NP-hard, so this algorithm typically does not scale to very large graphs.

Maximal Cliques of a Simple Undirected Graph

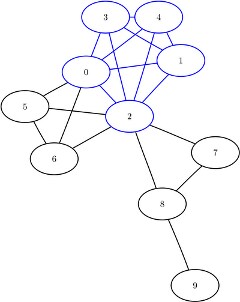
This section illustrates the use of the clique algorithm on the simple undirected graph G that is shown in Figure 1.46.

Figure 1.46: A Simple Undirected Graph G

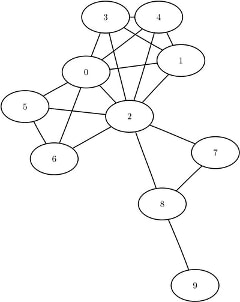
The undirected graph G can be represented by the following links data set LinkSetIn:

data LinkSetIn;
   input from to @@;
   datalines;
0 1  0 2  0 3  0 4  0 5
0 6  1 2  1 3  1 4  2 3
2 4  2 5  2 6  2 7  2 8
3 4  5 6  7 8  8 9
;

The following statements calculate the maximal cliques, output the results in the data set Cliques, and use the SQL procedure as a convenient way to create a table CliqueSizes of clique sizes:

proc optgraph
   data_links = LinkSetIn;
   clique
      out     = Cliques;
run;

proc sql;
   create table CliqueSizes as
   select clique, count(*) as size
   from Cliques
   group by clique
   order by size desc;
quit;

The data set Cliques now contains the maximal cliques of the input graph; it is shown in Figure 1.47.

Figure 1.47: Maximal Cliques of a Simple Undirected Graph

clique	node
1	0
1	2
1	1
1	3
1	4
2	0
2	2
2	5
2	6
3	2
3	8
3	7
4	8
4	9

In addition, the data set CliqueSizes contains the number of nodes in each clique; it is shown in Figure 1.48.

Figure 1.48: Sizes of Maximal Cliques of a Simple Undirected Graph

clique	size
1	5
2	4
3	3
4	2

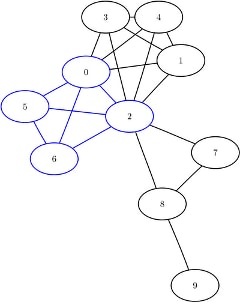
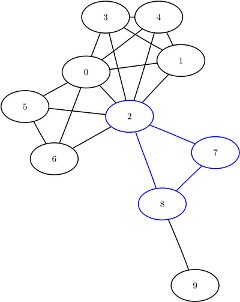
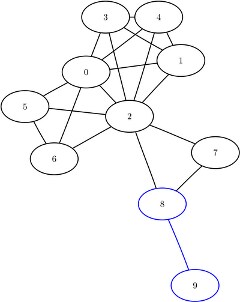
The maximal cliques are shown graphically in Figure 1.49 and Figure 1.50.

Figure 1.49: Maximal Cliques and

Figure 1.50: Maximal Cliques and