The OPTGRAPH Procedure
- Overview
-
Getting Started

-
Syntax
 Functional SummaryPROC OPTGRAPH StatementBICONCOMP StatementCENTRALITY StatementCLIQUE StatementCOMMUNITY StatementCONCOMP StatementCORE StatementCYCLE StatementDATA_LINKS_VAR StatementDATA_MATRIX_VAR StatementDATA_NODES_VAR StatementEIGENVECTOR StatementLINEAR_ASSIGNMENT StatementMINCOSTFLOW StatementMINCUT StatementMINSPANTREE StatementPERFORMANCE StatementREACH StatementSHORTPATH StatementSUMMARY StatementTRANSITIVE_CLOSURE StatementTSP Statement
Functional SummaryPROC OPTGRAPH StatementBICONCOMP StatementCENTRALITY StatementCLIQUE StatementCOMMUNITY StatementCONCOMP StatementCORE StatementCYCLE StatementDATA_LINKS_VAR StatementDATA_MATRIX_VAR StatementDATA_NODES_VAR StatementEIGENVECTOR StatementLINEAR_ASSIGNMENT StatementMINCOSTFLOW StatementMINCUT StatementMINSPANTREE StatementPERFORMANCE StatementREACH StatementSHORTPATH StatementSUMMARY StatementTRANSITIVE_CLOSURE StatementTSP Statement -
Details
 Graph Input DataMatrix Input DataData Input OrderParallel ProcessingNumeric LimitationsSize LimitationsCommon Notation and AssumptionsBiconnected Components and Articulation PointsCentralityCliqueCommunityConnected ComponentsCore DecompositionCycleEigenvector ProblemLinear Assignment (Matching)Minimum-Cost Network FlowMinimum CutMinimum Spanning TreeReach (Ego) NetworkShortest PathSummaryTransitive ClosureTraveling Salesman ProblemMacro VariablesODS Table Names
Graph Input DataMatrix Input DataData Input OrderParallel ProcessingNumeric LimitationsSize LimitationsCommon Notation and AssumptionsBiconnected Components and Articulation PointsCentralityCliqueCommunityConnected ComponentsCore DecompositionCycleEigenvector ProblemLinear Assignment (Matching)Minimum-Cost Network FlowMinimum CutMinimum Spanning TreeReach (Ego) NetworkShortest PathSummaryTransitive ClosureTraveling Salesman ProblemMacro VariablesODS Table Names -
Examples
 Articulation Points in a Terrorist NetworkInfluence Centrality for Project Groups in a Research DepartmentBetweenness and Closeness Centrality for Computer Network TopologyBetweenness and Closeness Centrality for Project Groups in a Research DepartmentEigenvector Centrality for Word Sense DisambiguationCentrality Metrics for Project Groups in a Research DepartmentCommunity Detection on Zachary’s Karate Club DataRecursive Community Detection on Zachary’s Karate Club DataCycle Detection for Kidney Donor ExchangeLinear Assignment Problem for Minimizing Swim TimesLinear Assignment Problem, Sparse Format versus Dense FormatMinimum Spanning Tree for Computer Network TopologyTransitive Closure for Identification of Circular Dependencies in a Bug Tracking SystemReach Networks for Computation of Market Coverage of a Terrorist NetworkTraveling Salesman Tour through US Capital Cities
Articulation Points in a Terrorist NetworkInfluence Centrality for Project Groups in a Research DepartmentBetweenness and Closeness Centrality for Computer Network TopologyBetweenness and Closeness Centrality for Project Groups in a Research DepartmentEigenvector Centrality for Word Sense DisambiguationCentrality Metrics for Project Groups in a Research DepartmentCommunity Detection on Zachary’s Karate Club DataRecursive Community Detection on Zachary’s Karate Club DataCycle Detection for Kidney Donor ExchangeLinear Assignment Problem for Minimizing Swim TimesLinear Assignment Problem, Sparse Format versus Dense FormatMinimum Spanning Tree for Computer Network TopologyTransitive Closure for Identification of Circular Dependencies in a Bug Tracking SystemReach Networks for Computation of Market Coverage of a Terrorist NetworkTraveling Salesman Tour through US Capital Cities - References
Graph Input Data
This section describes how to input a graph for analysis by PROC OPTGRAPH. Let ![]() define a graph with a set N of nodes and a set A of links.
define a graph with a set N of nodes and a set A of links.
Consider the directed graph shown in Figure 1.8.
Figure 1.8: A Simple Directed Graph
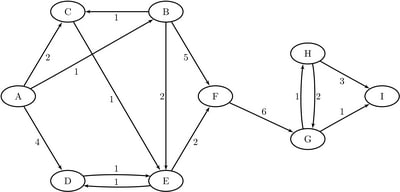
Notice that each node and link has associated attributes: a node label and a link weight.
Link Input Data
The DATA_LINKS= option in the PROC OPTGRAPH statement defines the data set that contains the list of links in the graph. A link is represented as a pair of nodes, which are defined by using either numeric or character labels. The links data set is expected to contain some combination of the following possible variables:
-
from: the from node (this variable can be numeric or character) -
to: the to node (this variable can be numeric or character) -
weight: the link weight (this variable must be numeric) -
weight2: the auxiliary link weight (this variable must be numeric) -
lower: the link flow lower bound (this variable must be numeric) -
upper: the link flow upper bound (this variable must be numeric)
As described in the GRAPH_DIRECTION= option, if the graph is undirected, the from and to labels are interchangeable. If the weights are not given for algorithms that call for link weights, they are all assumed to be 1.
The data set variable names can have any values that you want. If you use nonstandard names, you must identify the variables by using the DATA_LINKS_VAR statement, as described in the section DATA_LINKS_VAR Statement.
For example, the following two data sets identify the same graph:
data LinkSetInA; input from $ to $ weight; datalines; A B 1 A C 2 A D 4 ; data LinkSetInB; input source_node $ sink_node $ value; datalines; A B 1 A C 2 A D 4 ;
These data sets can be presented to PROC OPTGRAPH by using the following equivalent statements:
proc optgraph
data_links = LinkSetInA;
run;
proc optgraph
data_links = LinkSetInB;
data_links_var
from = source_node
to = sink_node
weight = value;
run;
The directed graph G shown in Figure 1.8 can be represented by the following links data set LinkSetIn:
data LinkSetIn; input from $ to $ weight @@; datalines; A B 1 A C 2 A D 4 B C 1 B E 2 B F 5 C E 1 D E 1 E D 1 E F 2 F G 6 G H 1 G I 1 H G 2 H I 3 ;
The following statements read in this graph, declare it as a directed graph, and output the resulting links and nodes data sets. These statements do not run any algorithms, so the resulting output contains only the input graph.
proc optgraph graph_direction = directed data_links = LinkSetIn out_nodes = NodeSetOut out_links = LinkSetOut; run;
The data set NodeSetOut, shown in Figure 1.9, now contains the nodes that are read from the input link data set. The variable node shows the label associated with each node.
The data set LinkSetOut, shown in Figure 1.10, contains the links that were read from the input link data set. The variables from and to show the associated node labels.
Figure 1.10: Link Data Set of a Simple Directed Graph
If you define this graph as undirected, then reciprocal links (for example, ![]() and
and ![]() ) are treated as the same link, and duplicates are removed. PROC OPTGRAPH takes the first occurrence of the link and ignores
the others. By default, GRAPH_DIRECTION=UNDIRECTED, so you can just remove this option to declare the graph as undirected.
) are treated as the same link, and duplicates are removed. PROC OPTGRAPH takes the first occurrence of the link and ignores
the others. By default, GRAPH_DIRECTION=UNDIRECTED, so you can just remove this option to declare the graph as undirected.
proc optgraph data_links = LinkSetIn out_nodes = NodeSetOut out_links = LinkSetOut; run;
The progress of the procedure is shown in Figure 1.11. The log now shows the links (and their observation identifiers) that were declared as duplicates and removed.
Figure 1.11: PROC OPTGRAPH Log: Link Data Set of a Simple Undirected Graph
| NOTE: ------------------------------------------------------------------------------------------ |
| NOTE: Running OPTGRAPH version 14.1. |
| NOTE: ------------------------------------------------------------------------------------------ |
| NOTE: The OPTGRAPH procedure is executing in single-machine mode. |
| NOTE: ------------------------------------------------------------------------------------------ |
| NOTE: Data input used 0.01 (cpu: 0.00) seconds. |
| WARNING: Link (E,D) in observation 9 of the DATA_LINKS= data set is a duplicate and is ignored. |
| WARNING: Link (H,G) in observation 14 of the DATA_LINKS= data set is a duplicate and is ignored. |
| NOTE: The number of nodes in the input graph is 9. |
| NOTE: The number of links in the input graph is 13. |
| NOTE: ------------------------------------------------------------------------------------------ |
| NOTE: Data output used 0.00 (cpu: 0.00) seconds. |
| NOTE: ------------------------------------------------------------------------------------------ |
| NOTE: The data set WORK.NODESETOUT has 9 observations and 1 variables. |
| NOTE: The data set WORK.LINKSETOUT has 13 observations and 3 variables. |
The data set NodeSetOut is equivalent to the one shown in Figure 1.9. However, the new links data set LinkSetOut shown in Figure 1.12 contains two fewer links than before, because duplicates are removed.
Figure 1.12: Link Data Set of a Simple Undirected Graph
Certain algorithms can perform more efficiently when you specify GRAPH_INTERNAL_FORMAT=THIN in the PROC OPTGRAPH statement. However, when you specify this option, PROC OPTGRAPH does not remove duplicate links. Instead, you should use appropriate DATA steps to clean your data before calling PROC OPTGRAPH.
Node Input Data
The DATA_NODES= option in the PROC OPTGRAPH statement defines the data set that contains the list of nodes in the graph. This data set is used to define clusters (subgraphs) or to assign node weights.
The nodes data set is expected to contain some combination of the following possible variables:
-
node: the node label (this variable can be numeric or character) -
cluster: the node cluster identifier (this variable must be numeric) -
weight: the node weight (this variable must be numeric) -
weight2: the auxiliary node weight (this variable must be numeric)
The variable cluster is used to define clusters (subgraphs) for decomposing the input graph into subgraphs for processing. This is useful for
the algorithms specified in the CENTRALITY, REACH, and SUMMARY statements. The use of the variable cluster is explained in more detail in the section Processing by Cluster.
You can specify any values that you want for the data set variable names. If you use nonstandard names, you must identify the variables by using the DATA_NODES_VAR statement, as described in the section DATA_NODES_VAR Statement.
The data set that is specified in the DATA_LINKS= option defines the set of nodes that are incident to some link. If the graph contains a node that has no links (called a singleton node), then this node must be defined in the DATA_NODES data set. The following is an example of a graph with three links but four nodes, including a singleton node D:
data NodeSetIn; input label $ @@; datalines; A B C D ; data LinkSetInS; input from $ to $ weight; datalines; A B 1 A C 2 B C 1 ;
If you specify duplicate entries in the node data set, PROC OPTGRAPH takes the first occurrence of the node and ignores the others. A warning is printed to the log.
Node Subset Input Data
For some algorithms, you might want to process only a subset of the nodes that appear in the input graph. You can accomplish this by using the DATA_NODES_SUB= option in the PROC OPTGRAPH statement. You can use the node subset data set in conjunction with the SHORTPATH or REACH statement. (See the sections Shortest Path and Reach (Ego) Network, respectively.) The node subset data set is expected to contain some combination of the following variables:
-
node: the node label (this variable can be numeric or character) -
source: whether to process this node as a source node in shortest path algorithms (this variable must be numeric) -
sink: whether to process this node as a sink node in shortest path algorithms (this variable must be numeric) -
reach: for the reach algorithm, the index of the source subgraph for processing (this variable must be numeric)
Table 1.53 shows how PROC OPTGRAPH processes nodes for each algorithm type. The missing indicator (.) can also be used in place of 0 to designate that a node is not to be processed.
Table 1.53: Determining How to Process a Node
|
Algorithm Type |
Variable Designations |
Example Shown In: |
|---|---|---|
|
Shortest path |
A value of 0 for the |
The section Shortest Path |
|
Reach |
A value of 0 for the |
The section Reach (Ego) Network |
A representative example of a node subset data set that might be used with the graph in Figure 1.8 is as follows:
data NodeSubSetIn; input node $ reach source sink; datalines; A 1 1 . F 2 . 1 E 2 1 . ;
The data set NodeSubSetIn indicates that you want to process the following:
-
the reach network from the subgraph defined by node A
-
the reach network from the subgraph defined by nodes F and E
-
the shortest paths for the source-sink pairs in
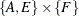
Standardized Labels
For large scale graphs, the processing stage that reads the nodes and links into memory can be time consuming. Under the following assumptions, you can use the STANDARDIZED_LABELS option in the PROC OPTGRAPH statement to greatly speed up this stage:
-
The link data set variables
fromandtoare numeric type -
The node and node subset data set variable
nodeis numeric type -
The node labels start from 0 and are consecutive nonnegative integers.
Consider the following links data set that uses numeric labels:
data LinkSetIn; input from to weight; datalines; 0 1 1 3 0 2 1 5 1 ;
Using default settings, the following statements echo back link and node data sets that contain three links and four nodes, respectively.
proc optgraph data_links = LinkSetIn out_nodes = NodeSetOut out_links = LinkSetOut; run;
The log is shown in Figure 1.13.
Figure 1.13: PROC OPTGRAPH Log: A Simple Undirected Graph
| NOTE: ------------------------------------------------------------------------------------------ |
| NOTE: Running OPTGRAPH version 14.1. |
| NOTE: ------------------------------------------------------------------------------------------ |
| NOTE: The OPTGRAPH procedure is executing in single-machine mode. |
| NOTE: ------------------------------------------------------------------------------------------ |
| NOTE: Data input used 0.01 (cpu: 0.00) seconds. |
| NOTE: The number of nodes in the input graph is 4. |
| NOTE: The number of links in the input graph is 3. |
| NOTE: ------------------------------------------------------------------------------------------ |
| NOTE: Data output used 0.00 (cpu: 0.00) seconds. |
| NOTE: ------------------------------------------------------------------------------------------ |
| NOTE: The data set WORK.NODESETOUT has 4 observations and 1 variables. |
| NOTE: The data set WORK.LINKSETOUT has 3 observations and 3 variables. |
The data set NodeSetOut, shown in Figure 1.14, contains the unique numeric node labels, ![]() .
.
Using standardized labels, the same input data set defines a graph with six (not four) nodes.
proc optgraph standardized_labels data_links = LinkSetIn out_nodes = NodeSetOut out_links = LinkSetOut; run;
The log that results from using standardized labels is shown in Figure 1.15.
Figure 1.15: PROC OPTGRAPH Log: A Simple Undirected Graph Using Standardized Labels
| NOTE: ------------------------------------------------------------------------------------------ |
| NOTE: Running OPTGRAPH version 14.1. |
| NOTE: ------------------------------------------------------------------------------------------ |
| NOTE: The OPTGRAPH procedure is executing in single-machine mode. |
| NOTE: ------------------------------------------------------------------------------------------ |
| NOTE: Data input used 0.00 (cpu: 0.00) seconds. |
| NOTE: The number of nodes in the input graph is 6. |
| NOTE: The number of links in the input graph is 3. |
| NOTE: The number of singleton nodes in the input graph is 2. |
| NOTE: ------------------------------------------------------------------------------------------ |
| NOTE: Data output used 0.00 (cpu: 0.00) seconds. |
| NOTE: ------------------------------------------------------------------------------------------ |
| NOTE: The data set WORK.NODESETOUT has 6 observations and 1 variables. |
| NOTE: The data set WORK.LINKSETOUT has 3 observations and 3 variables. |
The data set NodeSetOut, shown in Figure 1.16, now contains all node labels from 0 to 5, based on the assumptions when using the STANDARDIZED_LABELS option.
When using standardized labels, the DATA_NODES= input order (which can be arbitrary) is not preserved in the OUT_NODES= output data set. Instead, the order is ascending, starting from zero.