The OPTGRAPH Procedure

Core Decomposition

Subsections:

An alternative to community detection for detecting cohesive subgroups is a method for extracting k-cores, known as core decomposition. Although this method is generally not as powerful as community detection for extracting a detailed community structure, it can give a coarse approximation of cohesive structure at a very low computational cost. Let $G=(N,A)$ define a graph with nodes N and links A, and let $G_ S = (S,A_ S)$ be an induced subgraph on nodes S. The subgraph $G_ S$ is a k-core if and only if for every node $v \in S$, the degree of v is greater than or equal to k and $G_ S$ is the maximum subgraph with this property. By definition, the cores are nested. That is, if $G_{S_ k}$ is a k-core of size k, then $G_{S_{k+1}}$ is contained in $G_{S_ k}$.

In PROC OPTGRAPH, you can invoke core decomposition by using the CORE statement. The options for this statement are described in the section CORE Statement.

The results for the core decomposition algorithm are given in the output node data set that is specified in the OUT_NODES= option in the PROC OPTGRAPH statement. For each node in the node data set, the variable core_out identifies its core number, the highest-order core that contains this node. The core identifiers are numbered sequentially starting from 0.

The core decomposition algorithm reports status information in a macro variable called _OPTGRAPH_CORE_. See the section Macro Variable _OPTGRAPH_CORE_ for more information about this macro variable.

The algorithm used for core decomposition is based on the work presented in Batagelj and Zaversnik 2003. This algorithm runs in time $O(|A|)$ and therefore should scale to very large graphs.

Core Decomposition of a Simple Undirected Graph

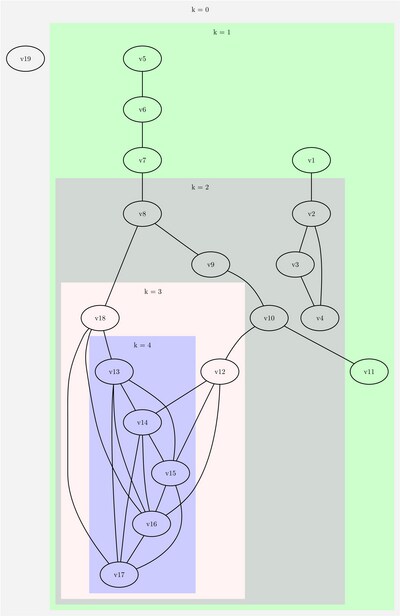
This section illustrates the use of the core decomposition algorithm on the simple undirected graph G that is shown in Figure 1.63.

Figure 1.63: Simple Undirected Graph

Simple Undirected Graph


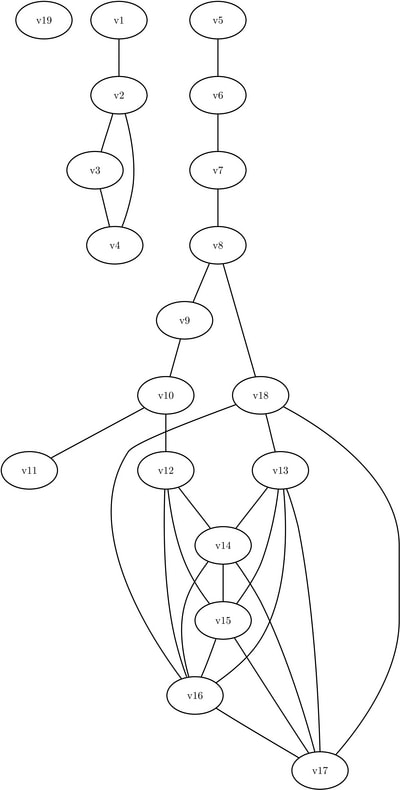
The undirected graph G can be represented using the following nodes data set NodeSetIn and links data set LinkSetIn: 

data NodeSetIn;
   input node $ @@;
   datalines;
v1    v2   v3   v4   v5
v6    v7   v8   v9  v10
v11  v12  v13  v14  v15
v16  v17  v18  v19
;

data LinkSetIn;
   input from $ to $ @@;
   datalines;
v1   v2   v5  v6   v6  v7   v7  v8  v10 v11
v2   v3   v3  v4   v2  v4   v8  v9   v9 v10
v8  v18  v10 v12  v13 v14  v13 v15  v13 v16
v13 v17  v14 v15  v14 v16  v14 v17  v15 v16
v15 v17  v16 v17  v18 v13  v18 v17  v18 v16
v12 v14  v12 v15  v12 v16
;

The following statements calculate the core decomposition and output the results in the data set NodeSetOut: 

proc optgraph
   data_nodes = NodeSetIn
   data_links = LinkSetIn
   out_nodes  = NodeSetOut;
   core;
run;

The node data set NodeSetOut contains the core number (variable core_out) for each node and is shown in Figure 1.64.

Figure 1.64: Core Decomposition of a Simple Undirected Graph

node core_out
v19 0
v1 1
v5 1
v6 1
v7 1
v11 1
v2 2
v3 2
v4 2
v8 2
v9 2
v10 2
v12 3
v18 3
v13 4
v14 4
v15 4
v16 4
v17 4 




               

               


               
Figure 1.65 shows the graph layered by its core number. 
               

               
  

               

                  
Figure 1.65: Core Decomposition

                  

                     
Core Decomposition