The OPTGRAPH Procedure

This example looks at the problem of assigning swimmers to strokes based on their best times. However, in this case certain swimmers are not eligible to perform certain strokes. A missing (.) value in the data matrix identifies an ineligible assignment. For example:

data RelayTimesMatrix;
   input name $ sex $ back breast fly free;
   datalines;
Sue     F   .  36.7 28.3 36.1
Karen   F 34.6    .    . 26.2
Jan     F 31.3    . 27.1    .
Andrea  F 28.6    . 29.1    .
Carol   F 32.9    . 26.6    .
;

Recall that the linear assignment problem can also be interpreted as the minimum-weight matching in a bipartite graph. The eligible assignments define links between the rows (swimmers) and the columns (strokes), as in Figure 1.149.

Figure 1.149: Bipartite Graph for Linear Assignment Problem

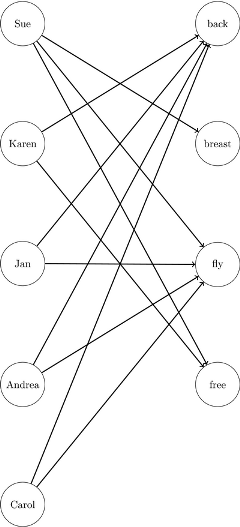
You can represent the same data in RelayTimesMatrix by using a links data set as follows:

data RelayTimesLinks;
   input name $ attr $ cost;
   datalines;
Sue     breast 36.7
Sue     fly    28.3
Sue     free   36.1
Karen   back   34.6
Karen   free   26.2
Jan     back   31.3
Jan     fly    27.1
Andrea  back   28.6
Andrea  fly    29.1
Carol   back   32.9
Carol   fly    26.6
;

This graph must be bipartite (such that S and T are disjoint). If it is not, PROC OPTGRAPH returns an error.

Now, you can use either input format to solve the same problem, as follows:

proc optgraph
   data_matrix = RelayTimesMatrix;
   linear_assignment
      out      = LinearAssignMatrix
      weight   = (back--free)
      id       = (name sex);
run;

proc optgraph
   graph_direction = directed
   data_links      = RelayTimesLinks;
   data_links_var
      from         = name
      to           = attr
      weight       = cost;
   linear_assignment
      out          = LinearAssignLinks;
run;

When you use the graph input format, the LINEAR_ASSIGNMENT options WEIGHT= and ID= are not used directly.

The data sets LinearAssignMatrix and LinearAssignLinks now contain the optimal assignments, as shown in Output 1.11.1 and Output 1.11.2.

The optimal assignments are shown graphically in Figure 1.150.

Figure 1.150: Optimal Assignments for Swim Times

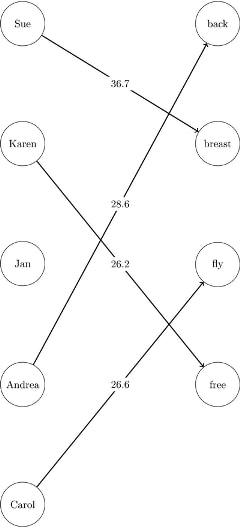
For large problems where a number of links are forbidden, the sparse format can be faster and can save a great deal of memory. Consider an example that uses the format of the DATA_MATRIX= option with 15,000 columns () and 4,000 rows (). To store the dense matrix in memory, PROC OPTGRAPH needs to allocate approximately MB. If the data have mostly ineligible links, then the sparse (graph) format that uses the DATA_LINKS= option is much more efficient with respect to memory. For example, if the data have only 5% of the eligible links (), then the dense storage would still need 457 MB. The sparse storage for the same example needs approximately MB. If the problem is fully dense (all links are eligible), then the dense format that uses the DATA_MATRIX= option is the most efficient.