The OPTGRAPH Procedure

In many languages, numerous words are polysemous (they carry more than one meaning). A common task in information retrieval is to assign the correct meaning to a polysemous word within a given context. Take the word "bass" as an example. It can mean either a type of fish (as in the sentence "I went fishing for some sea bass") or tones of low frequency (as in the sentence "The bass part of the song is very moving").

The following example from Mihalcea 2005 shows how eigenvector centrality can be used to disambiguate the word sense in the sentence "The church bells no longer ring on Sundays." The following senses of words can be drawn from a dictionary:

Using one of the similarity metrics defined in Sinha and Mihalcea 2007, you can generate a graph in which the nodes correspond to the word senses given above and the weights are determined by the similarity metric. The resulting graph is shown in Figure 1.143.

Figure 1.143: Eigenvector Centrality for Word Sense Disambiguation

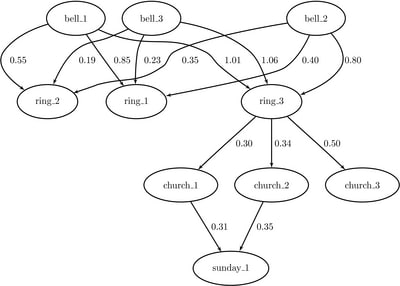
To identify the correct senses, you run eigenvector centrality on the graph and select the highest ranking sense for each word:

data LinkSetIn;
   input from $ to $ weight;
   datalines;
bell_1   ring_1   0.85
bell_1   ring_2   0.55
bell_1   ring_3   1.01
bell_2   ring_1   0.40
bell_2   ring_2   0.35
bell_2   ring_3   0.80
bell_3   ring_1   0.23
bell_3   ring_2   0.19
bell_3   ring_3   1.06
ring_3   church_1 0.30
ring_3   church_2 0.34
ring_3   church_3 0.50
church_1 sunday_1 0.31
church_2 sunday_1 0.35
;

proc optgraph
   data_links = LinkSetIn
   out_nodes  = NodeSetOut;
   centrality
      eigen   = weight;
run;

data NodeSetOut;
   length word $8 sense $1;
   set NodeSetOut;
   word  = scan(node,1,'_');
   sense = scan(node,2,'_');
run;

proc sort
   data = NodeSetOut
   out  = WordSenses;
   by word descending centr_eigen_wt;
run;

data WordSenses;
   set WordSenses(drop=centr_eigen_wt);
   by word;
   if first.word then output;
run;

The eigenvector scores and the implied word sense are shown in Output 1.5.1.