The SSM Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 State Space Model and NotationTypes of Sequence DataOverview of Model Specification SyntaxFiltering, Smoothing, Likelihood, and Structural Break DetectionEstimation of User-Specified Linear Combination of State ElementsContrasting PROC SSM with Other SAS Procedures Predefined Trend ModelsPredefined Structural ModelsCovariance ParameterizationMissing ValuesComputational IssuesDisplayed OutputODS Table NamesODS Graph NamesOUT= Data Set
State Space Model and NotationTypes of Sequence DataOverview of Model Specification SyntaxFiltering, Smoothing, Likelihood, and Structural Break DetectionEstimation of User-Specified Linear Combination of State ElementsContrasting PROC SSM with Other SAS Procedures Predefined Trend ModelsPredefined Structural ModelsCovariance ParameterizationMissing ValuesComputational IssuesDisplayed OutputODS Table NamesODS Graph NamesOUT= Data Set -
Examples
 Bivariate Basic Structural Model Panel Data: Random-Effects and Autoregressive ModelsBackcasting, Forecasting, and InterpolationLongitudinal Data: Smoothing of Repeated MeasuresA User-Defined Trend ModelModel with Multiple ARIMA ComponentsDynamic Factor ModelingDiagnostic Plots and Structural Break AnalysisLongitudinal Data: Variable Bandwidth SmoothingA Transfer Function Model for the Gas Furnace DataPanel Data: Dynamic Panel Model for the Cigar DataMultivariate Modeling: Long-Term Temperature TrendsBivariate Model: Sales of Mink and Muskrat FursFactor Model: Now-Casting the US EconomyLongitudinal Data: Lung Function Analysis
Bivariate Basic Structural Model Panel Data: Random-Effects and Autoregressive ModelsBackcasting, Forecasting, and InterpolationLongitudinal Data: Smoothing of Repeated MeasuresA User-Defined Trend ModelModel with Multiple ARIMA ComponentsDynamic Factor ModelingDiagnostic Plots and Structural Break AnalysisLongitudinal Data: Variable Bandwidth SmoothingA Transfer Function Model for the Gas Furnace DataPanel Data: Dynamic Panel Model for the Cigar DataMultivariate Modeling: Long-Term Temperature TrendsBivariate Model: Sales of Mink and Muskrat FursFactor Model: Now-Casting the US EconomyLongitudinal Data: Lung Function Analysis - References
The STATE statement specifies a subsection of ![]() , the overall state vector at time t (for more information, see the section State Space Model and Notation). Consider the state equations that define the state space model:
, the overall state vector at time t (for more information, see the section State Space Model and Notation). Consider the state equations that define the state space model:
You can specify multiple STATE statements, each specifying a separate subsection. It is assumed that the subsections that
are specified by using different STATE statements are mutually independent. This independence assumption implies a block-diagonal
structure for the transition matrices ![]() and the disturbance covariances
and the disturbance covariances ![]() for all
for all ![]() . An appropriate block structure also applies to
. An appropriate block structure also applies to ![]() and
and ![]() . The options in the STATE statement provide complete control over the description of the relevant blocks of
. The options in the STATE statement provide complete control over the description of the relevant blocks of ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . The argument dim (a positive integer in name (dim)) specifies the nominal dimension of this subsection. In most situations, the nominal dimension and the actual dimension
of the state subsection are the same. However, when you specify the TYPE=
option, the actual dimension of the state subsection can be different from the nominal dimension. The TYPE=
option simplifies the state specification task for some commonly needed models.
. The argument dim (a positive integer in name (dim)) specifies the nominal dimension of this subsection. In most situations, the nominal dimension and the actual dimension
of the state subsection are the same. However, when you specify the TYPE=
option, the actual dimension of the state subsection can be different from the nominal dimension. The TYPE=
option simplifies the state specification task for some commonly needed models.
Note: The T
, COV
, W
, and COV1
options, described later in this section, specify the relevant blocks of ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , respectively. The structure of these matrix blocks is described in a similar way in the option descriptions. For example,
the specification COV(I) corresponds to the identity form, COV(D) corresponds to the diagonal form, and COV(G) corresponds
to the general form of the
, respectively. The structure of these matrix blocks is described in a similar way in the option descriptions. For example,
the specification COV(I) corresponds to the identity form, COV(D) corresponds to the diagonal form, and COV(G) corresponds
to the general form of the ![]() block.
block.
You can use the following options in the STATE statement to specify the system matrices ![]() ,
, ![]() ,
, ![]() , and
, and ![]() and to request printing of their estimates when they contain unknown parameters. You can also request the checking of unexpected
changes—structural breaks—in the evolution of this state subsection by using the CHECKBREAK
option.
and to request printing of their estimates when they contain unknown parameters. You can also request the checking of unexpected
changes—structural breaks—in the evolution of this state subsection by using the CHECKBREAK
option.
- A1(nd)
-
specifies that the last nd elements of the state subsection be treated as diffuse. This becomes the dimension of the relevant subsection of the diffuse vector
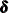 . The
. The 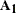 block is created by using appropriate columns of the identity matrix. The value of nd must lie between 1 and the nominal dimension, dim. The absence of this option signifies that this subsection of
block is created by using appropriate columns of the identity matrix. The value of nd must lie between 1 and the nominal dimension, dim. The absence of this option signifies that this subsection of 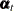 is nondiffuse. If both the COV1
and A1 options are specified, the last nd rows and columns of the matrix specified in the COV1 option are taken to be 0. This option cannot be used together with the
RANK= option of the COV1
option.
is nondiffuse. If both the COV1
and A1 options are specified, the last nd rows and columns of the matrix specified in the COV1 option are taken to be 0. This option cannot be used together with the
RANK= option of the COV1
option.
- CHECKBREAK<( ELEMENTWISE | OVERALL)>
-
turns on the checking of breaks for this state subsection. The ELEMENTWISE suboption requests the elementwise checking of any unexpected change in the state subsection as it evolves from one time point to the next. The OVERALL suboption requests a similar check for the entire state subsection—that is, in this case the change is measured as a multidimensional change. The ELEMENTWISE suboption is the default. Unless the PRINT=BREAKDETAIL option is specified, only a summary of the most significant breaks is produced. If the PRINT=BREAKDETAIL is specified, tables that contain the break significance statistics at every distinct time point are produced—one for the ELEMENTWISE suboption and one for the OVERALL suboption. For more information about the structural break detection process, see the section Structural Breaks in the State Evolution. For an example of the use of the CHECKBREAK option, see Example 27.8.
-
COV( D ) <= (var1 var2 ...) | (number1 number2 ...)>
COV( G ) <= (var1 var2 ...) | (number1 number2 ...)>
COV( I ) <= (variable) | (number)>
COV( RANK=integer ) -
specifies the relevant block of the disturbance covariance
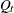 (for
(for 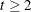 ) in the transition equation. As with the T
option, the absence of this option signifies that this Q-block consists of only zeros. The structure of the Q-block is also
similarly specified. However, the following differences exist:
) in the transition equation. As with the T
option, the absence of this option signifies that this Q-block consists of only zeros. The structure of the Q-block is also
similarly specified. However, the following differences exist:
-
The list that is specified to form the covariance must result in a symmetric, positive semidefinite matrix. For an example, see Example 27.5.
-
You can specify a rank constraint on the Q-block by specifying COV(RANK=integer), where the specified integer must lie between 1 and dim. A rank constraint is permissible only for the general form and only when its elements are not specified by using a list.
-
The convention of treating unset variables as structural zeros, which is used in specifying sparsity of the T-block, is not used in the Q-block specification. Whenever you explicitly specify the entries of the Q-block by specifying a list of variables in parentheses, all variables in the list must evaluate to nonmissing values.
The following examples illustrate different ways of specifying a Q-block. It is assumed that dim = 2.
-
COV(G) specifies a general-form Q-block, which contributes
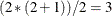 unspecified elements to the parameter vector
unspecified elements to the parameter vector 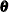 .
.
-
COV(RANK=1) specifies a rank-one Q-block.
-
-
COV1( D ) <= (var1 var2 ...) | (number1 number2 ...)>
COV1( G ) <= (var1 var2 ...) | (number1 number2 ...)>
COV1( I ) <= (variable) | (number)>
COV1( RANK=integer ) -
specifies the relevant block of the initial state covariance
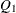 . The different options in this case have the same meaning as the options of the COV
option. However, the following differences exist:
. The different options in this case have the same meaning as the options of the COV
option. However, the following differences exist:
-
If the elements of
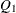 are specified by a list of variables in parentheses, then these variables must evaluate to constant values. In particular,
they can depend on parameters that are specified by the PARMS statements; however, they cannot depend on any of the input
data columns.
are specified by a list of variables in parentheses, then these variables must evaluate to constant values. In particular,
they can depend on parameters that are specified by the PARMS statements; however, they cannot depend on any of the input
data columns.
-
If the initial condition is partially diffuse (that is, the diffuse dimension nd specified in the A1 option is nonzero), the last nd rows and columns of the matrix specified in COV1 are taken to be zero. Moreover, if the elements of
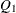 are specified by a list, its number of elements must correspond to a matrix of dimension (dim – nd).
are specified by a list, its number of elements must correspond to a matrix of dimension (dim – nd).
-
-
PRINT=AR | BREAKDETAIL | COV | COV1 | MA | T
PRINT=(<AR> <BREAKDETAIL> <COV> <COV1> <MA> <T> ) -
requests printing of the respective system matrices and the printing of the break statistics at each distinct time point. You can specify PRINT=AR or PRINT=MA only if you specify the TYPE=VARMA option. If any of these matrices are time-varying, the matrix that corresponds to the first time instance is printed. For the BREAKDETAIL suboption to have any effect, the CHECKBREAK option must be turned on. If TYPE= option is used, the result of PRINT=COV can be different than the matrix supplied in the COV= option.
- SINPUT = (var1 var2 ...) | (number1 number2 ...)
-
specifies the relevant dim-dimensional block of the state input vector
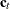 . The absence of this option signifies that this block of the
. The absence of this option signifies that this block of the 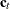 vector consists of only zeros. If the elements of
vector consists of only zeros. If the elements of 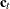 are specified by a list of variables in parentheses, then these variables must be independent of unknown parameters. In particular,
they cannot be functions of parameters that are defined by the PARMS statements.
are specified by a list of variables in parentheses, then these variables must be independent of unknown parameters. In particular,
they cannot be functions of parameters that are defined by the PARMS statements.
-
T( D ) <= (var1 var2 ...) | (number1 number2 ...)>
T( G ) <= (var1 var2 ...) | (number1 number2 ...)>
T( I ) <= (variable) | (number)> -
specifies the relevant block of the transition matrix
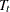 . The absence of this option signifies that this block consists of only zeros. You can specify the structure of the T-block
by specifying T(I) for the identity form, T(D) for the diagonal form, and T(G) for a general unstructured form. In addition,
you can explicitly specify the entries of the T-block by specifying a list of numbers in parentheses, or by specifying in
parentheses a list of variables that are defined by using the programming statements. The unspecified elements of the T-block
are included in the list of parameters to be estimated from the data. If the elements of the T-block are supplied by a list
in parentheses, the number of elements in the list depends on its structure. For the diagonal form, the list must contain
exactly dim elements. In the case of the identity form—T(I)—the block is already fully specified; however, a specification T(I)=(variable) is understood to mean that the identity block is scaled by the specified variable (or a number). In the general case—T(G)—the list must consist of
. The absence of this option signifies that this block consists of only zeros. You can specify the structure of the T-block
by specifying T(I) for the identity form, T(D) for the diagonal form, and T(G) for a general unstructured form. In addition,
you can explicitly specify the entries of the T-block by specifying a list of numbers in parentheses, or by specifying in
parentheses a list of variables that are defined by using the programming statements. The unspecified elements of the T-block
are included in the list of parameters to be estimated from the data. If the elements of the T-block are supplied by a list
in parentheses, the number of elements in the list depends on its structure. For the diagonal form, the list must contain
exactly dim elements. In the case of the identity form—T(I)—the block is already fully specified; however, a specification T(I)=(variable) is understood to mean that the identity block is scaled by the specified variable (or a number). In the general case—T(G)—the list must consist of 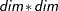 elements, specified in a rowwise fashion. An inappropriate number of elements in the list results in a syntax error.
elements, specified in a rowwise fashion. An inappropriate number of elements in the list results in a syntax error.
The following examples illustrate different ways of specifying the transition matrix. It is assumed that dim = 2.
-
T(I) specifies that the T-block is a two-dimensional identity matrix.
-
T(D) specifies that the T-block is a two-dimensional diagonal matrix. The two unspecified diagonal entries become part of the parameter vector
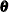 .
.
-
T(D)=(1.1 2) fully specifies the two-dimensional diagonal T-block.
-
T(D)=(
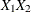 ) specifies a two-dimensional diagonal T-block where the diagonal elements are dynamically calculated based on the values
of the variables
) specifies a two-dimensional diagonal T-block where the diagonal elements are dynamically calculated based on the values
of the variables 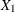 and
and 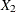 . In this case the T-block can change with time if
. In this case the T-block can change with time if 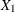 or
or 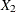 changes with time.
changes with time.
-
T(G) specifies a general form T-block (with
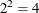 unspecified elements).
unspecified elements).
-
T(G)=(
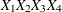 ) specifies a general form T-block where the first row is formed by
) specifies a general form T-block where the first row is formed by 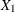 and
and 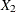 , and the second row is formed by
, and the second row is formed by 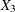 and
and 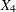 .
.
In practice the transition matrix is often sparse—that is, many of its elements are 0. The algorithms in the SSM procedure exploit this sparsity structure for computational efficiency. Whenever you explicitly specify the entries of the T-block by specifying a list of variables in parentheses, you can leave the variables that correspond to the zero elements unset. These unset variables are treated as structural zeros by the SSM procedure. The section Sparse Transition Matrix Specification further explains how to use this sparsity convention.
-
-
TYPE=WN
TYPE=RW
TYPE=LL (SLOPECOV(I | D | G) <= (var1, var2, ...) | (number1, number2, ...)> )
TYPE=LL (SLOPECOV( RANK=integer) )
TYPE=SEASON (LENGTH=integer <DROPH=number-list> <KEEPH=number-list> )
TYPE=CYCLE <( <CT> <RHO=variable | number> <PERIOD=variable | number> )>
TYPE=VARMA ( <p <(I | D)> =integer> <q<(D)>=integer> ) -
specifies a state subsection that corresponds to the specified type. You can specify either a number or a variable for the RHO= and PERIOD= suboptions. When TYPE=VARMA, the autoregressive and moving average orders can be at most 1 (
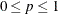 and
and 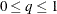 ). Moreover, by using the D and I flags with the order specification, you can impose additional structure on the autoregressive
and moving average coefficient matrices—for example, specifying TYPE=VARMA(P=1) implies a VAR(1) model with general autoregressive
coefficient matrix, whereas specifying TYPE=VARMA(P(D)=1) implies a VAR(1) model with diagonal autoregressive coefficient
matrix. If you specify the TYPE= option, the T
, COV1
, SINPUT
, and A1
options are not needed. In fact they are ignored, since the transition matrix
). Moreover, by using the D and I flags with the order specification, you can impose additional structure on the autoregressive
and moving average coefficient matrices—for example, specifying TYPE=VARMA(P=1) implies a VAR(1) model with general autoregressive
coefficient matrix, whereas specifying TYPE=VARMA(P(D)=1) implies a VAR(1) model with diagonal autoregressive coefficient
matrix. If you specify the TYPE= option, the T
, COV1
, SINPUT
, and A1
options are not needed. In fact they are ignored, since the transition matrix 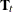 and the matrices in the initial condition (
and the matrices in the initial condition (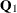 and
and 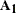 ) are implicitly defined by the choice of the type. However, the COV
and W
options can be useful. In fact, the specification of the COV
option does play a key role in the eventual form of
) are implicitly defined by the choice of the type. However, the COV
and W
options can be useful. In fact, the specification of the COV
option does play a key role in the eventual form of 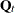 —the covariance of the disturbance term in the transition equation. For the types LL, CYCLE, SEASON, and VARMA, the dimension
of the resulting state subsection is a certain multiple of dim, the nominal dimension in the STATE statement. For example, the following specification results in a state subsection, named
—the covariance of the disturbance term in the transition equation. For the types LL, CYCLE, SEASON, and VARMA, the dimension
of the resulting state subsection is a certain multiple of dim, the nominal dimension in the STATE statement. For example, the following specification results in a state subsection, named
cycleState, of dimension 2*dim:state cycleState(dim) cov(g) type=cycle;The name
cycleStatecorresponds to the state underlying a dim-dimensional cycle component. All of these special state types require that the data be regular (replication is permissible); the only exception is TYPE=CYCLE(CT), which defines a continuous-time cycle and is applicable to any data type. Table 27.2 summarizes some of this information for easy reference. For more information about these state types, see the section Predefined Structural Models.The TYPE=LL specification results in a state that corresponds to a multivariate local linear trend. It is governed by two covariance matrices: the COV option specifies the covariance that corresponds to the level equation, and the SLOPECOV suboption specifies the covariance used in the slope equation. The form of the SLOPECOV suboption is exactly the same as that of the COV option.
The TYPE=CYCLE option results in a state that corresponds to a (stochastic) cycle. By default, this cycle is assumed to be for the regular data type. If TYPE=CYCLE(CT), the resulting cycle is applicable to any data type. The CT option is available only for dim = 1; that is, only a univariate cycle is available for the irregular data type. The cycle specification depends on a covariance matrix and two numbers: the damping factor RHO and the cycle period PERIOD. The covariance can be specified by the COV option. The damping factor is specified by the RHO= suboption; its value must lie between 0.0 and 1.0. The cycle period can be specified by the PERIOD= suboption. If the CT suboption is not included, the period value must be larger than 2.0. On the other hand, if the CT suboption is included, its value must be strictly positive. If these parameters are not specified, they are estimated from the data.
The TYPE=SEASON(LENGTH=integer) specifies a multivariate trigonometric season that contains the full set of harmonics (for more information, see Multivariate Season). In some cases, you might want to drop some of the harmonics from this complete set to obtain a more parsimonious trigonometric season specification. You can use the DROPH= (to drop) or KEEPH= (to keep) suboption to control the harmonics that are included in the season specification as follows:
-
TYPE=SEASON(
-
LENGTH=integer
-
<DROPH=number-list | n TO m BY p>
-
<KEEPH=number-list | n TO m BY p>
-
)
The DROPH= and KEEPH= lists can include any integer between 1 and LENGTH/2 if the season length is even and any integer between 1 and (LENGTH – 1)/2 if the season length is odd. For example, the following specification results in a specification of a trigonometric season with a season length 12 that consists of only the first four harmonics
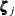 ,
, 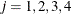 :
:
type=season(length=12 DROPH=5 6) ...;The last two high-frequency harmonics,
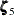 and
and 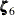 , are dropped. The DROPH= suboption cannot be used with the KEEPH= suboption.
, are dropped. The DROPH= suboption cannot be used with the KEEPH= suboption.
Table 27.2: Summary of Predefined State Types
Type
Description
Parameters
State Dimension
WN
dim-variate white noise
dim
RW
dim-variate random walk
dim
LL
dim-variate local linear
COV , SLOPECOV
2*dim
SEASON(LENGTH=length)
dim-variate season
(length–1)*dim
CYCLE
dim-variate cycle
COV , RHO, PERIOD
2*dim
VARMA(P=p Q=q)
dim-variate VARMA(p, q)
COV , AR, MA
dim*max( p, q+1)
-
-
W( D )= (var1 var2 ...)
W( G )= (var1 var2 ...)
W( I )= (variable) -
specifies the relevant block of the design matrix
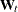 in the transition equation. The W-block is of dimension
in the transition equation. The W-block is of dimension 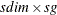 , where sdim denotes the actual dimension of the state subsection (which can be the same as dim, the nominal dimension, or different if the TYPE=
option is used) and sg denotes the desired size of the subsection of the overall state regression vector
, where sdim denotes the actual dimension of the state subsection (which can be the same as dim, the nominal dimension, or different if the TYPE=
option is used) and sg denotes the desired size of the subsection of the overall state regression vector 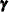 . As with the T
option, the absence of this option signifies that this W-block consists of only zeros. The structure of the W-block is also
similarly specified. The number of variables supplied in the W(G)= list option must be a multiple of sdim. For example, if sdim = 4 and the W(G)= list contains 8 variables, then the implied size of
. As with the T
option, the absence of this option signifies that this W-block consists of only zeros. The structure of the W-block is also
similarly specified. The number of variables supplied in the W(G)= list option must be a multiple of sdim. For example, if sdim = 4 and the W(G)= list contains 8 variables, then the implied size of 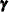 subsection is 2. If the W(D)= or W(I)= option is used, then the W-block is assumed to be an
subsection is 2. If the W(D)= or W(I)= option is used, then the W-block is assumed to be an 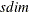 -dimensional diagonal matrix and the W(D)= list must contain exactly sdim variables. For examples of the use of this option, see Example 27.8, Example 27.10, and Example 27.11.
-dimensional diagonal matrix and the W(D)= list must contain exactly sdim variables. For examples of the use of this option, see Example 27.8, Example 27.10, and Example 27.11.