The SSM Procedure

Example 27.7 Dynamic Factor Modeling

This example shows how you can fit the dynamic Nelson-Siegel (DNS) factor model discussed in Koopman, Mallee, and van der Wel (2010). The following DATA step creates the yield-curve data set, Dns, that is used in this article. The data are monthly bond yields that were recorded between the start of 1970 to the end of 2000 for 17 bonds of different maturities; the maturities range from three months to 10 years (120 months). The variable date contains the observation date, yield contains the bond yield, maturity contains the associated bond maturity, and mtype contains an index (ranging from 1 to 17) that sequentially labels bonds of increasing maturity. The data have been extended for two more years by adding missing yields for the years 2001 and 2002, which causes the SSM procedure to produce model forecasts for this span.

data Dns;
input date : date. yield maturity mtype;
format date date.;
datalines;
1-Jan-70    8.019    3    1
1-Jan-70    8.091    6    2
1-Jan-70    8.108    9    3

   ... more lines ...

In addition, suppose you are interested in extrapolating the fitted model to predict the yield of a hypothetical bond that has a maturity of 42 months and is not traded on the general exchange. The following DATA step creates the necessary missing values for this new bond, which is assigned the index of 18—that is, the value of mtype is 18.

data tmp1;
   set dns(keep=date);
   by date;
   if first.date then do;
       yield = .;
       maturity = 42;
       mtype = 18;
       output;
   end;
run;

 proc append data=tmp1 base=dns; run;
 proc sort data=dns;
 by date;
 run;

Suppose that $\theta _{t}(\tau )$ denotes the (idealized) yield at time t that is associated with a bond of maturity $\tau$ (in months). Even if time is not measured continuously and the bonds of only certain maturities are traded, $\theta _{t}(\tau )$ is treated as a smooth function of two continuous variables, time t and maturity $\tau$ . Koopman, Mallee, and van der Wel (2010) discuss a variety of models for $\theta _{t}(\tau )$ , which is called the yield surface. One of these models depends on a positive, time-varying, scalar parameter $\lambda _{t}$ and a time-varying three-dimensional vector parameter $\pmb {\beta }_{t}$ . This model can be described as follows:

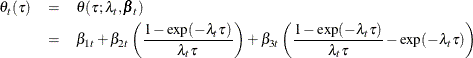
$\begin{eqnarray*} \theta _{t}(\tau ) & = & \theta (\tau ; \lambda _{t}, \pmb {\beta }_{t}) \nonumber \\ & = & \beta _{1t} + \beta _{2t} \left( \frac{1 - \exp (-\lambda _{t} \tau )}{\lambda _{t} \tau } \right) + \beta _{3t} \left( \frac{1 - \exp (-\lambda _{t} \tau )}{\lambda _{t} \tau } - \exp (-\lambda _{t} \tau ) \right) \nonumber \end{eqnarray*}$

This model is a dynamic version of a static model discussed in Nelson and Siegel (1987), where $\lambda _{t}$ and $\pmb {\beta }_{t}$ are time invariant. For fixed time period t, the three terms in this model have relatively simple interpretation. The first term $\beta _{1t}$ can be thought of as the overall yield level because it does not depend on $\tau$ , the bond maturity. It can also be thought of as the long term yield because as $\tau \uparrow \infty$ the other two terms vanish; the coefficients of both $\beta _{2t}$ and $\beta _{3t}$ converge to 0 as $\tau \uparrow \infty$ (recall that $\lambda _{t}$ is positive). Next, note that as $\tau \downarrow 0$ the coefficient of $\beta _{2t}$ in the second term converges to 1 while that of $\beta _{3t}$ in the third term converges to 0; therefore the second term can be thought of as a correction to the overall yield that is associated with the short term bonds. Finally, note that the coefficient of $\beta _{3t}$ in the third term is a unimodal function of $\tau$ that decays monotonically to 0 as $\tau \downarrow 0$ and as $\tau \uparrow \infty$ ; therefore the third term is associated with the medium term bond yields. It is postulated that the observed yield, denoted by $y_{t}(\tau )$ , is a noisy version of this unobserved (true) yield $\theta _{t}(\tau )$ . The observed yield can be modeled as

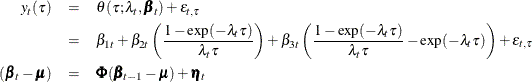
$\begin{eqnarray*} y_{t}(\tau ) & = & \theta (\tau ; \lambda _{t}, \pmb {\beta }_{t}) + \epsilon _{t, \tau } \nonumber \\ & = & \beta _{1t} + \beta _{2t} \left( \frac{1 - \exp (-\lambda _{t} \tau )}{\lambda _{t} \tau } \right) + \beta _{3t} \left( \frac{1 - \exp (-\lambda _{t} \tau )}{\lambda _{t} \tau } - \exp (-\lambda _{t} \tau ) \right) + \epsilon _{t, \tau } \nonumber \\ (\pmb {\beta }_{t} - \pmb {\mu }) & = & \pmb {\Phi } (\pmb {\beta }_{t-1} - \pmb {\mu }) + \pmb {\eta }_{t} \nonumber \end{eqnarray*}$

where $\epsilon _{t, \tau }$ are zero-mean, independent, Gaussian variables with variance $\sigma ^{2}_{\tau }$ , and $\pmb {\eta }_{t}$ is a three-dimensional, Gaussian white noise. That is, $\pmb {\beta }_{t}$ is a VAR(1) process with mean vector $\pmb {\mu }$ . The remainder of this example explains how to use the SSM procedure to fit this model to the yield data in the Dns data set.

Suppose that variables Z1, Z2, and Z3 are defined as the coefficients of $\beta _{1t}$ , $\beta _{2t}$ , and $\beta _{3t}$ , respectively. That is,

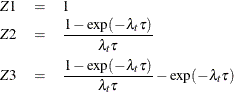
$\begin{eqnarray*} Z1 & = & 1 \nonumber \\ Z2 & = & \frac{1 - \exp (-\lambda _{t} \tau )}{\lambda _{t} \tau } \nonumber \\ Z3 & = & \frac{1 - \exp (-\lambda _{t} \tau )}{\lambda _{t} \tau } - \exp (-\lambda _{t} \tau ) \nonumber \end{eqnarray*}$

In this case,

$\theta _{t}(\tau ) = Z1* \beta _{1t} + Z2* \beta _{2t} + Z3* \beta _{3t}$

Let $\pmb {\zeta }_{t} = \pmb {\beta }_{t} - \pmb {\mu }$ . Then $\pmb {\zeta }_{t}$ is a zero-mean VAR(1) process and $\pmb {\beta }_{t} = \pmb {\zeta }_{t} + \pmb {\mu }$ . In particular,

$\begin{eqnarray*} \theta _{t}(\tau ) & = & Z1*\beta _{1t} + Z2*\beta _{2t} + Z3*\beta _{3t} \nonumber \\ & = & Z1* \zeta _{1t} + Z2* \zeta _{2t} + Z3* \zeta _{3t} + Z1* \mu _{1} + Z2* \mu _{2} + Z3* \mu _{3} \nonumber \end{eqnarray*}$

This shows that the model for $y_{t}(\tau )$ can be cast into a state space form with the following observation equation:

$y_{t}(\tau ) = \mb{Z} \pmb {\zeta }_{t} + \mb{Z} \pmb {\mu } + \epsilon _{t, \tau }$

The underlying six-dimensional state vector $\pmb {\alpha }_{t}$ is formed by joining the two independent subvectors, $\pmb {\zeta }_{t}$ (which is a zero-mean, VAR(1) process) and the constant mean vector $\pmb {\mu }$ . That is, $\pmb {\alpha }_{t} = ( \zeta _{1t} \; \zeta _{2t} \; \zeta _{3t} \; \mu _{1} \; \mu _{2} \; \mu _{3})^{'}$ .

Note that the variables Z2 and Z3 depend on the time varying parameter $\lambda _{t}$ , which is unknown. $\lambda _{t}$ is assumed to be a smooth and positive function of time t. In what follows $\lambda _{t}$ is represented as an exponential of a cubic spline—a B-spline— in time with four evenly spaced interior knots between January 1970 and December 2002. A cubic spline with four interior knots can be represented as a sum of seven (number of knots + spline degree + 1) B-spline basis functions, $c_{1t}, c_{2t}, \ldots , c_{7t}$ , for example. More specifically, $\lambda _{t}$ can be expressed as

$\lambda _{t} = \exp ( v1*c_{1t} + \ldots + v7*c_{7t} )$

for some parameters $v1, v2, \ldots , v7$ and the B-spline basis functions (of time) $c_{1t}, c_{2t}, \ldots , c_{7t}$ . Thus, the variables Z2 and Z3 become known functions of time, except for the parameters $v1, v2, \ldots , v7$ , which are estimated from the data. The following statements augment the Dns data set with the B-spline basis columns in two steps. First a data set that contains the basis columns, c1–c7, is created by using the BSPLINE function in the IML procedure. This data set is then merged with the Dns data set.

 proc iml;
    use dns;
    read all var {date} into x;
    bsp = bspline(x, 2, ., 4);
    create spline var{c1 c2 c3 c4 c5 c6 c7};
    append from bsp;
 quit;
 data dns;
    merge dns spline;
 run;

The following statements use the SSM procedure to perform the model fitting and forecasting calculations. The variance of the observation equation disturbance for the hypothetical bond (mtype = 18) is taken to be the average of the neighboring bonds (mtype = 10 and 11), whose maturities are 36 and 48 months, respectively.

  proc ssm data=Dns optimizer(technique=dbldog maxiter=400);
       id date interval=month;

      /* Time-varying parameter lambda */
      parms v1-v7;
      lambda = exp(v1*c1 + v2*c2 + v3*c3 + v4*c4
           + v5*c5 + v6*c6 + v7*c7);

      /* Observation equation disturbance -- separate variance for each maturity */
      parms sigma1-sigma17 / lower=1.e-4;
      array s_array(17) sigma1-sigma17;
       do i=1 to 17;
          if (mtype=i) then sigma = s_array[i];
       end;
       if (mtype=18) then sigma = (sigma10+sigma11)/2;
       irregular wn variance=sigma;

       /* Variables Z1, Z2, Z3 needed in the observation equation */
       Z1= 1.0;
       tmp = lambda*maturity;
       Z2 = (1-exp(-tmp))/tmp;
       Z3 = ( 1-exp(-tmp)-tmp*exp(-tmp) )/tmp;

        /* Zero-mean VAR(1) factor zeta and the associated component */
       state zeta(3) type=VARMA(p(d)=1) cov(g) print=(cov ar);
       comp zetaComp = (Z1-Z3)*zeta;

       /* Constant mean vector mu and the associated component */
        state mu(3) type=rw;
        comp muComp = (Z1-Z3)*mu;

        /* Observation equation */
        model yield = muComp zetaComp wn;

        /* Various components defined only for output purposes  */
        eval yieldSurface = muComp + zetaComp;

        comp zeta1 = zeta[1];
        comp zeta2 = zeta[2];
        comp zeta3 = zeta[3];
        comp mu1 = mu[1];
        comp mu2 = mu[2];
        comp mu3 = mu[3];

        comp z2zeta = (Z2)*zeta[2];
        comp z3zeta = (Z3)*zeta[3];
        comp z2Mu =  (Z2)*mu[2];
        comp z3Mu =  (Z3)*mu[3];

        eval beta1 = mu1 + zeta1;
        eval beta2 = mu2 + zeta2;
        eval beta3 = mu3 + zeta3;

        eval shortTem = z2zeta + z2Mu;
        eval medTerm = z3zeta + z3Mu;

        /* output the component estimates and the forecasts */
        output out=dnsFor pdv;
    run;

The DBLDOG optimization technique is used for parameter estimation since it is computationally more efficient in this example. The transition matrix, $\pmb {\Phi }$ , in the VAR(1) specification of $\pmb {zeta}$ is taken to be diagonal (TYPE=VARMA(P(D)=1)) because the use of more general square matrix did not improve the model fit significantly. The mean vector $\pmb {mu}$ (recall that $\pmb {beta}_{t} = \pmb {zeta}_{t} + \pmb {mu}$ ) is specified as a three-dimensional random walk with zero disturbance covariance (signified by the absence of COV= option). The model specification part of the program ends with the MODEL statement; the subsequent COMP and EVAL statements define some useful linear combinations of the underlying state. Their estimates are computed after the model fit is completed and are output to the output data set dnsFor. The dnsFor data set also contains all the program variables and the parameters defined in the PARMS statement because the OUTPUT statement contains the PDV option.

Output 27.7.1 shows the estimated mean vector ( $\pmb {\mu }$ ). It shows that the mean long-term yield is 7.64. Output 27.7.2 shows the estimates of v1–v7 (used for defining time-varying $\lambda _{t}$ ) and the maturity specific observation variances. Output 27.7.3 shows the estimate of the VAR(1) transition matrix $\pmb {\Phi }$ , and Output 27.7.4 shows the associated disturbance covariance matrix $\pmb {\Sigma }$ . The model fit summary is shown in Output 27.7.5.

Output 27.7.1: Estimate of the Mean Vector ( $\pmb {\mu }$ )

The SSM Procedure

Estimates of Fixed State Effects
State	Element Index	Estimate	Standard Error	t Value	Pr > \|t\|
mu	1	7.639	1.356	5.63	<.0001
mu	2	-1.319	0.777	-1.70	0.0895
mu	3	-0.309	0.268	-1.16	0.2481

Output 27.7.2: Estimates of v1–v7 and Observation Variances

Estimates of Named Parameters
Parameter	Estimate	Standard Error
v1	-1.19587	0.304003
v2	-2.93679	0.111440
v3	-1.88709	0.068972
v4	-2.31371	0.079116
v5	-3.21875	0.105575
v6	-1.66055	0.315692
v7	-4.60122	1.548096
sigma1	0.05406	0.004708
sigma2	0.00349	0.000865
sigma3	0.00869	0.000752
sigma4	0.01093	0.000901
sigma5	0.00865	0.000757
sigma6	0.00603	0.000571
sigma7	0.00519	0.000491
sigma8	0.00542	0.000497
sigma9	0.00562	0.000500
sigma10	0.00639	0.000559
sigma11	0.01032	0.000848
sigma12	0.00742	0.000676
sigma13	0.01106	0.000947
sigma14	0.01194	0.001051
sigma15	0.01244	0.001162
sigma16	0.02140	0.001842
sigma17	0.02746	0.002295

Output 27.7.3: Transition Matrix, $\pmb {\Phi }$ , Associated with $\pmb {\zeta }$

AR Coefficient Matrix for zeta
	Col1	Col2	Col3
Row1	0.98982	0	0
Row2	0	0.962457	0
Row3	0	0	0.803017

Output 27.7.4: Estimated Disturbance Covariance of $\pmb {\zeta }$

Disturbance Covariance for zeta
	Col1	Col2	Col3
Row1	0.108107	-0.02618	0.087107
Row2	-0.02618	0.360656	0.008928
Row3	0.087107	0.008928	1.072137

Output 27.7.5: Likelihood Computation Summary for the DNS Factor Model

Likelihood Computation Summary
Statistic	Value
Nonmissing Response Values Used	6324
Estimated Parameters	33
Initialized Diffuse State Elements	3
Normalized Residual Sum of Squares	6320.907
Diffuse Log Likelihood	3548.9546
Profile Log Likelihood	3547.4952

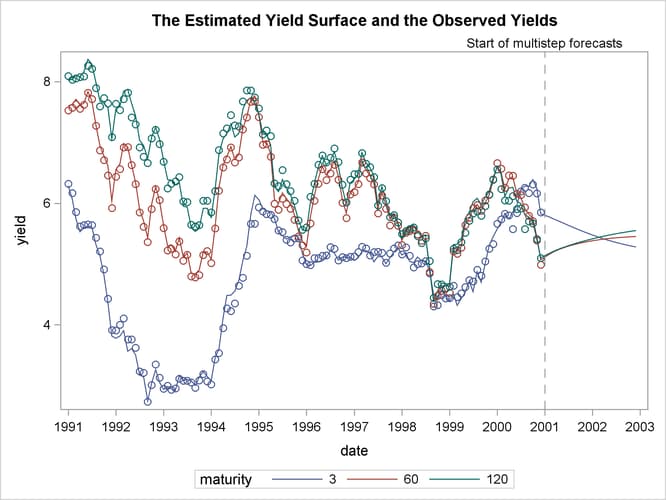
The following statements produce the time series plots of the smoothed estimate of the idealized bond yield ( $\theta _{t}(\tau )$ ) for bonds with maturities 30, 60, and 120 months (shown in Output 27.7.6). To simplify the display, the plots exclude the time span prior to 1991.

 proc sgplot data= dnsFor;
     title "The Estimated Yield Surface and the Observed Yields ";
     where maturity in (3 60 120) and date >= '31dec1990'd;
     series x=date y=smoothed_yieldSurface / group=maturity;
     scatter x=date y=yield / group=maturity;
     refline '31dec2000'd / axis=x lineattrs=GraphReference(pattern = Dash)
         name="RefLine"   label="Start of multistep forecasts";
 run;

Output 27.7.6: Smoothed Estimate of $\theta _{t}(\tau )$ for $\tau =3, 60, 120$

Smoothed Estimate of θt() for =3, 60, 120

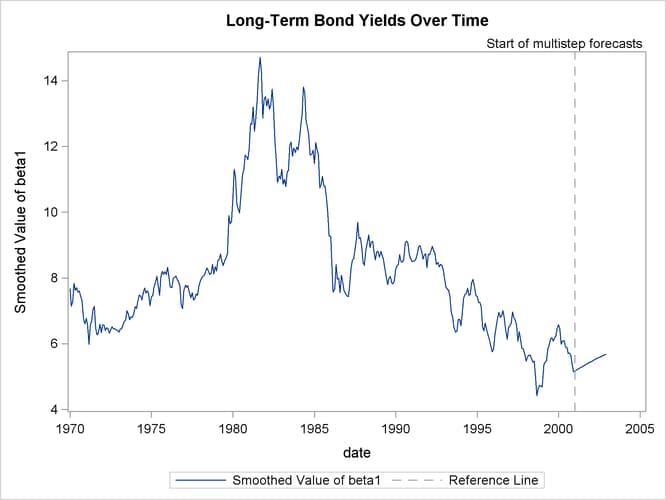
The plots indicate that the DNS model is a reasonable description of the yield data. Similar plots (not shown here) for other maturities also indicate the adequacy of the DNS model. The following statements produce the time series plot of the smoothed estimate of $\beta _{1t}$ , the long-term bond yield (shown in Output 27.7.7) :

 proc sgplot data=dnsFor;
    title "Long-Term Bond Yields Over Time ";
    series x=date y=smoothed_beta1 ;
    refline '31dec2000'd / axis=x lineattrs=GraphReference(pattern = Dash)
         name="RefLine"   label="Start of multistep forecasts";
 run;

Output 27.7.7: Smoothed Estimate of $\beta _{1t}$ , the Long-Term Yield

Smoothed Estimate of 1t, the Long-Term Yield

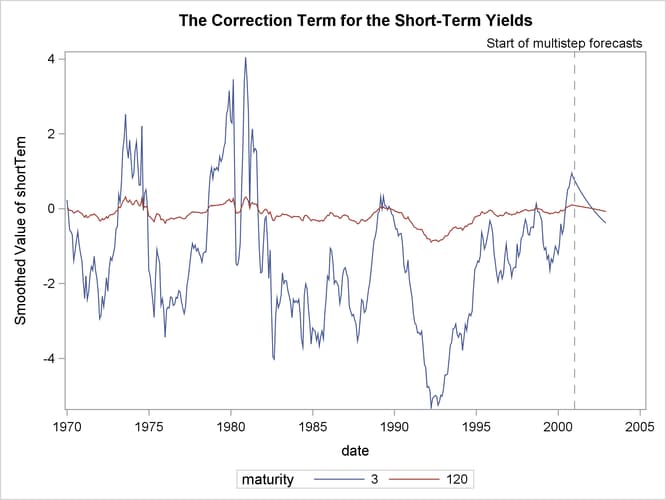
Similarly, Output 27.7.8, which is produced by the following statements, shows the smoothed estimate of the correction to the overall yield that is provided by the second term ( $Z2*\beta _{2t}$ ) for maturities of 3 months and 120 months. As expected, the correction for the (long-term) maturity of 120 months is negligible compared to the (short-term) maturity of 3 months.

 proc sgplot data=dnsFor;
   title "The Correction Term for the Short-Term Yields ";
   where maturity in (3 120);
   series x=date y=smoothed_shortTem / group=maturity;
   refline '31dec2000'd / axis=x lineattrs=GraphReference(pattern = Dash)
         name="RefLine"   label="Start of multistep forecasts";
 run;

Output 27.7.8: Smoothed Estimate of $Z2*\beta _{2t}$ , the Correction Term for the Short-Term Yields

Smoothed Estimate of Z2*2t, the Correction Term for the Short-Term Yields

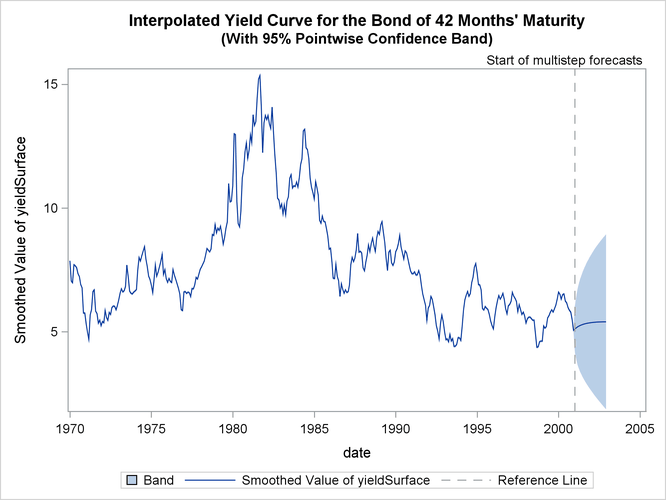
The following statements create plots that show the estimated yield for the hypothetical bond whose maturity is 42 months:

proc sgplot data=dnsFor;
   title "Interpolated Yield Curve for the Bond of 42 Months' Maturity";
   title2 "(With 95% Pointwise Confidence Band)";
   where maturity in (42);
   band x=date lower=smoothed_lower_yieldSurface upper=smoothed_upper_yieldSurface;
   series x=date y=smoothed_yieldSurface;
   refline '31dec2000'd / axis=x lineattrs=GraphReference(pattern = Dash)
      name="RefLine"   label="Start of multistep forecasts";
run;

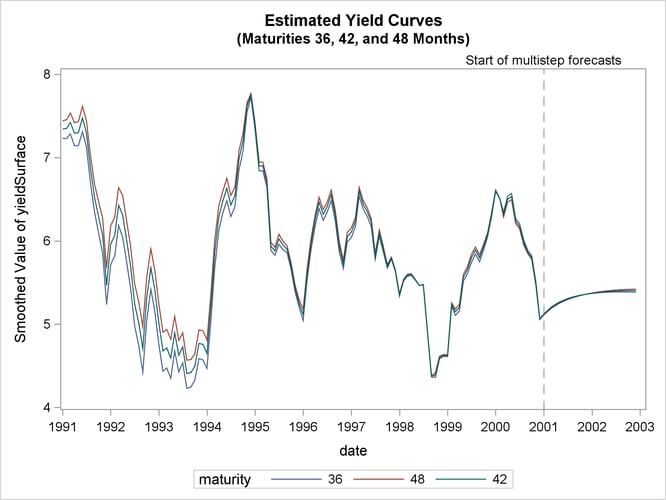
proc sgplot data= dnsFor;
  title "Estimated Yield Curves";
  title2 "(Maturities 36, 42, and 48 Months)";
  where maturity in (36 42 48) and date >= '31dec1990'd;
  series x=date y=smoothed_yieldSurface / group=maturity;
  refline '31dec2000'd / axis=x lineattrs=GraphReference(pattern = Dash)
      name="RefLine"   label="Start of multistep forecasts";
run;

Output 27.7.9 shows the interpolated yield curve with a pointwise 95% confidence band. In the historical period, the confidence band appears too tight, mostly because of graphical scaling.

Output 27.7.9: Interpolated Yield Curve for 42 Months’ Maturity

Output 27.7.10: Estimated Yield Curves

Output 27.7.10 shows the estimates of $\theta _{t}(\tau )$ for $\tau$ = 36, 42, and 48 months. As expected, the estimated $\theta _{t}(42)$ lies between the estimates of $\theta _{t}(36)$ and $\theta _{t}(48)$ .