The SSM Procedure

Example 27.13 Bivariate Model: Sales of Mink and Muskrat Furs

This example considers a bivariate time series of logarithms of the annual sales of mink and muskrat furs by the Hudson’s Bay Company for the years 1850–1911. These data have been analyzed previously by many authors, including Chan and Wallis (1978); Harvey (1989); Reinsel (1997). There is known to be a predator-prey relationship between the mink and muskrat species: minks are principal predators of muskrats. The previous analyses for these data generally conclude the following:

An increase in the muskrat population is followed by an increase in the mink population a year later, and an increase in the mink population is followed by a decrease in the muskrat population a year later.
Because muskrats are not the only item in the mink diet, and both mink and muskrat populations are affected by many other factors, the model must include additional terms to explain the year-to-year variation.

The analysis in this example, which loosely follows the discussion in Harvey (1989, chap. 8, sec. 8), also leads to similar conclusions. It begins by taking Harvey’s model 8.8.8 (a and b), with autoregressive order one, as the starting model—that is, assume that the bivariate (mink, muskrat) process $\mb{Y}_{t}$ satisfies the following relation:

$\begin{equation*} \begin{aligned} \pmb {\mu }_{t} & = \pmb {\mu }_{t-1} + \pmb {\beta } + \pmb {\nu }_{t} \\ \mb{Y}_{t} & = \pmb {\mu }_{t} + \pmb {\Phi } \mb{Y}_{t-1} + \pmb {\xi }_{t} \end{aligned}\end{equation*}$

This model postulates that $\mb{Y}_{t}$ can be expressed as a sum of three terms: $\pmb {\mu }_{t}$ , a bivariate trend that is modeled as a random walk with drift $\pmb {\beta }$ ; $\pmb {\Phi } \mb{Y}_{t-1}$ , an AR(1) correction; and $\pmb {\xi }_{t}$ , a bivariate Gaussian white noise disturbance. It is assumed that the AR coefficient matrix $\pmb {\Phi }$ is stable (that is, its eigenvalues are less than 1 in magnitude) and the bivariate disturbances $\pmb {\nu }_{t}$ (white noise associated with $\pmb {\mu }_{t}$ ) and $\pmb {\xi }_{t}$ are mutually independent. By noting that $\mb{Y}_{t} = \pmb {\Phi } \mb{Y}_{t-1} + \pmb {\mu }_{t-1} + \pmb {\beta } + \pmb {\nu }_{t} + \pmb {\xi }_{t}$ , you can formulate this model as a state space model (SSM) as follows:

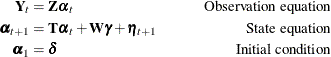
$\begin{equation*} \begin{aligned} \mb{Y}_{t} & = \mb{Z} \pmb {\alpha }_{t} & \qquad \text {Observation equation} \\ \pmb {\alpha }_{t+1} & = \mb{T} \pmb {\alpha }_{t} + \mb{W} \pmb {\gamma } + \pmb {\eta }_{t+1} & \qquad \text {State equation}\\ \pmb {\alpha }_{1} & = \pmb {\delta } & \qquad \text {Initial condition} \end{aligned}\end{equation*}$

The different parts of the SSM are as follows: the 4-dimensional state vector $\pmb {\alpha }_{t} = (\pmb {\mu }_{t}; \mb{Y}_{t})$ , the $2 \times 4$ –dimensional matrix in the observation equation $\mb{Z} = (\mb{0}\; \; \mb{I})$ , the $4 \times 4$ –dimensional transition matrix $\mb{T} = ( \mb{I} \; \; \mb{0}; \mb{I} \; \; \pmb {\Phi } )$ , the 4-dimensional state disturbance vector $\pmb {\eta }_{t} = (\pmb {\nu }_{t} ; \pmb {\nu }_{t} + \pmb {\xi }_{t})$ , the $4 \times 2$ -dimensional matrix $\mb{W} = (\mb{I}; \mb{I})$ , and the state regression vector $\pmb {\gamma } = \pmb {\beta }$ (the drift term in the equation of $\pmb {\mu }_{t}$ ). Here the matrices are specified in blocked form, with the rows separated by semicolons, and $\mb{I}$ and $\mb{0}$ denote the 2-dimensional identity and zero matrix, respectively. If $\mr{Cov}(\pmb {\nu }_{t}) = \Sigma _{1}$ and $\mr{Cov}(\pmb {\xi }_{t}) = \Sigma _{2}$ , the covariance of the state disturbance $\pmb {\eta }_{t}$ is given by $\mb{Q} = ( \Sigma _{1} \; \; \Sigma _{1}; \Sigma _{1} \; \; \Sigma _{1}+\Sigma _{2})$ , because $\pmb {\eta }_{t} = (\pmb {\nu }_{t} ; \pmb {\nu }_{t} + \pmb {\xi }_{t})$ , and $\pmb {\nu }_{t}$ and $\pmb {\xi }_{t}$ are mutually independent. A few points to note about this SSM formulation:

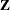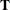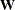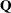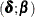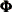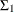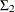The system matrices ( $\mb{Z}$ , $\mb{T}$ , $\mb{W}$ , and $\mb{Q}$ ) are time-invariant; the initial condition is totally diffuse (formed by the 6-dimensional vector $( \pmb {\delta }; \pmb {\beta } )$ ); and the elements of $\pmb {\Phi }$ , $\Sigma _{1}$ , and $\Sigma _{2}$ constitute the parameters of the model.
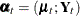The observation equation does not contain any noise or regression terms, which is typical of SSMs in which the response variables are part of the state vector: $\pmb {\alpha }_{t} = (\pmb {\mu }_{t}; \mb{Y}_{t})$ .

The following statements show how you can specify this model in the SSM procedure:

proc ssm data=furs plots=residual;

   /* Specify the ID variable */
   id year interval=year;

   /* Define parameters */
   parms phi11 phi12 phi21 phi22;
   parms rho1 rho2/ lower=-0.9999 upper=0.9999;
   parms msd1 msd2 esd1 esd2 / lower=1.e-8;

   /* Define variables used to form T, W, and Q */
   array tmat{4,4};
   tmat[1,1] = 1; tmat[2,2] = 1;
   tmat[3,1] = 1; tmat[3,3] = phi11; tmat[3,4] = phi12;
   tmat[4,2] = 1; tmat[4,3] = phi21; tmat[4,4] = phi22;

   array qmat{4,4};
   qmat[1,1]=msd1*msd1; qmat[1,2]=msd1*msd2*rho1;
   qmat[1,3]=qmat[1,1]; qmat[1,4]=qmat[1,2];
   qmat[2,1]=qmat[1,2]; qmat[2,2]=msd2*msd2;
   qmat[2,3]=qmat[1,2]; qmat[2,4]=qmat[2,2];
   qmat[3,1]=qmat[1,3]; qmat[3,2]=qmat[2,3];
   qmat[3,3]=qmat[1,1]+esd1*esd1;
   qmat[3,4]=qmat[1,2]+esd1*esd2*rho2;
   qmat[4,1]=qmat[1,4]; qmat[4,2]=qmat[2,4];
   qmat[4,3]=qmat[3,4]; qmat[4,4]=qmat[2,2]+esd2*esd2;

   array wmat{4,2};
   wmat[1,1] = 1; wmat[1,2] = 0; wmat[2,1] = 0; wmat[2,2] = 1;
   wmat[3,1] = 1; wmat[3,2] = 0; wmat[4,1] = 0; wmat[4,2] = 1;

   /* Specify the state equation */
   state alpha(4) t(g)=(tmat) w(g)=(wmat) cov(g)=(qmat) a1(4) print=(T cov);

   /* Specify the components used in the observation equation  */
   comp minkVal = alpha[3];
   comp muskVal = alpha[4];

   /* Specify the observation equation */
   model LogMink = minkVal;
   model LogMusk = muskVal;

   /* Specify components for output purposes: elements of trend mu */
   comp minkLevel = alpha[1];
   comp muskLevel = alpha[2];

   /* Specify an output data set to store component estimates */
   output out=salesFor press;
run;

The different parts of the program are explained as follows:

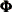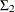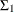The first PARMS statement defines phi11, phi12, phi21, and phi22 as model parameters. They represent the elements of $\pmb {\Phi }$ . Similarly, subsequent PARMS statements define additional parameters, which are used to form the elements of $\Sigma _{1}$ and $\Sigma _{2}$ . $\Sigma _{1}$ is parameterized as (msd1*msd1 msd1*msd2*rho1; msd1*msd2*rho1 msd2*msd2).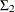 $\Sigma _{2}$ is similarly parameterized by using esd1, esd2, and rho2. 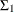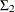This parameterization ensures that $\Sigma _{1}$ and $\Sigma _{2}$ are positive semidefinite. The model assumes that $\pmb {\Phi }$ is stable. The parameterization that this program uses does not impose this restriction.
The next several statements, such as the ARRAY statement, define lists of variables that are subsequently used in the specification of 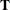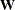$\mb{T}$ , $\mb{W}$ , and $\mb{Q}$ .
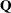The STATE statement defines a 4-dimensional state subsection (in fact, the entire state vector in the case of this example), named alpha.

The table in Output 27.13.1 shows the estimate of the drift vector $\pmb {\beta }$ in the equation of $\pmb {\mu }_{t}$ ( $\pmb {\mu }_{t} = \pmb {\mu }_{t-1} + \pmb {\beta } + \pmb {\nu }_{t}$ ).

Output 27.13.1: The Estimate of the Drift Vector $\pmb {\beta }$

Estimate of the State Equation Regression Vector
State	Element Index	Estimate	Standard Error	t Value	Pr > \|t\|
alpha	1	-0.000817	0.0323	-0.03	0.9798
alpha	2	0.005953	0.0258	0.23	0.8175

Clearly, both elements of $\pmb {\beta }$ are statistically insignificant, and the $\pmb {\mu }_{t}$ equation can be simplified as $\pmb {\mu }_{t} = \pmb {\mu }_{t-1} + \pmb {\nu }_{t}$ . Next, the table in Output 27.13.2 shows the estimates of the elements of $\pmb {\Phi }$ , $\Sigma _{1}$ , and $\Sigma _{2}$ .

Output 27.13.2: Estimates of $\pmb {\Phi }$ , $\Sigma _{1}$ , and $\Sigma _{2}$

Estimates of Named Parameters
Parameter	Estimate	Standard Error
phi11	-0.0011	0.1730
phi12	0.3349	0.1369
phi21	-0.9905	0.1419
phi22	0.6570	0.1208
rho1	0.8310	0.1377
rho2	-0.9999	1.6555
msd1	0.2500	0.0354
msd2	0.1991	0.0592
esd1	0.0662	0.0597
esd2	0.1344	0.0527

This table shows the following:

phi11, the first element of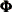 $\pmb {\Phi }$ , which relates the current value of LogMink with its lagged value, is statistically insignificant. That is, phi11 could be restricted to 0.
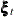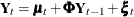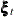rho2, the correlation coefficient between the elements of $\pmb {\xi }_{t}$ —the bivariate noise vector in the equation $\mb{Y}_{t} = \pmb {\mu }_{t} + \pmb {\Phi } \mb{Y}_{t-1} + \pmb {\xi }_{t}$ —is very near its lower boundary of –1 (in such cases the standard error of the parameter estimate is not reliable). This implies that the two elements of $\pmb {\xi }_{t}$ are perfectly negatively correlated.

Taken together, these observations suggest the reduced model

$\begin{equation*} \begin{aligned} \pmb {\mu }_{t} & = \pmb {\mu }_{t-1} + \pmb {\nu }_{t} \\ \mb{Y}_{t} & = \pmb {\mu }_{t} + \pmb {\Phi } \mb{Y}_{t-1} + \pmb {\xi }_{t} \end{aligned}\end{equation*}$

where $\pmb {\Phi } = (0 \; \; \phi _{12};\; \phi _{21} \; \; \phi _{22})$ and $\mr{Cov}(\pmb {\xi }_{t}) = \Sigma _{2}$ is parameterized as (esd1*esd1 -esd1*esd2; -esd1*esd2 esd2*esd2). The program that produces the reduced model is a simple modification of the preceding program and is not shown.

Output 27.13.3: Estimates of $\pmb {\Phi }$ , $\Sigma _{1}$ , and $\Sigma _{2}$ (Reduced Model)

Estimates of Named Parameters
Parameter	Estimate	Standard Error
phi12	0.3303	0.0986
phi21	-0.9973	0.1168
phi22	0.6680	0.1003
rho1	0.8526	0.0978
msd1	0.2472	0.0282
msd2	0.1955	0.0365
esd1	0.0679	0.0385
esd2	0.1372	0.0328

The table in Output 27.13.3 shows the new parameter estimates. By examining the parameter estimates, you can easily see that this model supports the general conclusions mentioned at the start of this example. In particular, note the following:

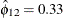$\hat{\phi }_{12} = 0.33$ implies that this year’s mink abundance is positively correlated with last year’s muskrat abundance.
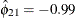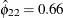$\hat{\phi }_{21} = -0.99$ and $\hat{\phi }_{22} = 0.66$ imply that this year’s muskrat abundance is negatively correlated with last year’s mink abundance and positively correlated with last year’s muskrat abundance.
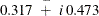Even though the parameters were not restricted to ensure stability, the estimated $\pmb {\Phi }$ turns out to be stable with a pair of complex eigenvalues, $0.317 \; \stackrel{-}{+}\; i \; 0.473$ , and a modulus of 0.570 (these calculations are done separately by using the IML procedure).
The fact that elements of 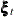$\pmb {\xi }_{t}$ are perfectly negatively correlated further supports the predator-prey relationship.

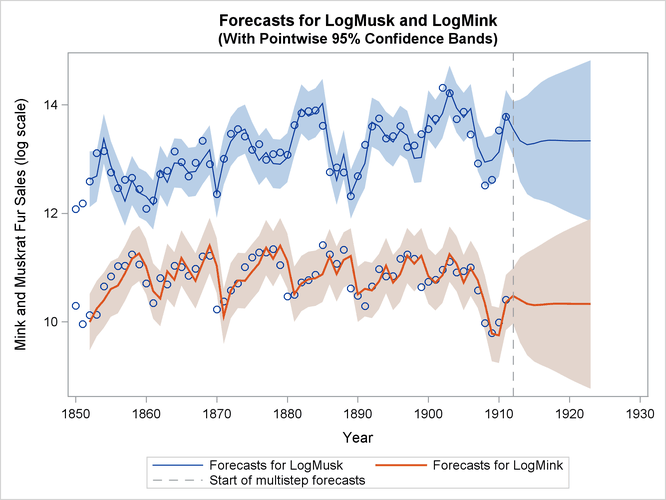
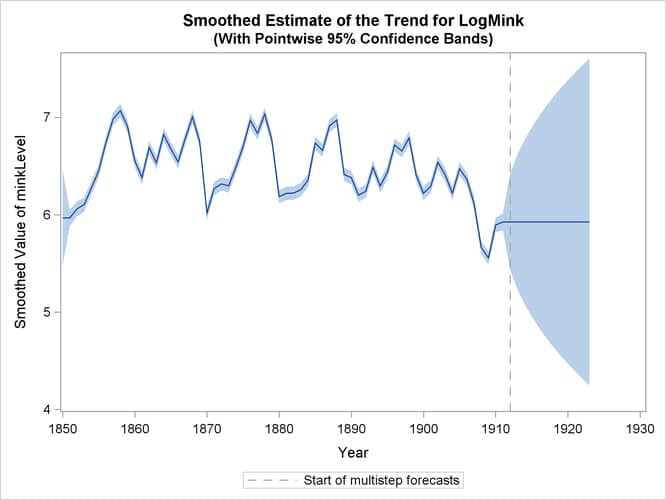
Finally, Output 27.13.4 shows the plots of one-step-ahead and post-sample forecasts for LogMink and LogMusk, and Output 27.13.5 shows the plot of the smoothed (full-sample) estimate of the first element of $\pmb {\mu }_{t}$ : LogMink Trend.

Output 27.13.4: Forecasts for Mink and Muskrat Fur Sales in Logarithms

Output 27.13.5: Smoothed Estimate of LogMink Trend