The SSM Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 State Space Model and NotationTypes of Sequence DataOverview of Model Specification SyntaxFiltering, Smoothing, Likelihood, and Structural Break DetectionEstimation of User-Specified Linear Combination of State ElementsContrasting PROC SSM with Other SAS Procedures Predefined Trend ModelsPredefined Structural ModelsCovariance ParameterizationMissing ValuesComputational IssuesDisplayed OutputODS Table NamesODS Graph NamesOUT= Data Set
State Space Model and NotationTypes of Sequence DataOverview of Model Specification SyntaxFiltering, Smoothing, Likelihood, and Structural Break DetectionEstimation of User-Specified Linear Combination of State ElementsContrasting PROC SSM with Other SAS Procedures Predefined Trend ModelsPredefined Structural ModelsCovariance ParameterizationMissing ValuesComputational IssuesDisplayed OutputODS Table NamesODS Graph NamesOUT= Data Set -
Examples
 Bivariate Basic Structural Model Panel Data: Random-Effects and Autoregressive ModelsBackcasting, Forecasting, and InterpolationLongitudinal Data: Smoothing of Repeated MeasuresA User-Defined Trend ModelModel with Multiple ARIMA ComponentsDynamic Factor ModelingDiagnostic Plots and Structural Break AnalysisLongitudinal Data: Variable Bandwidth SmoothingA Transfer Function Model for the Gas Furnace DataPanel Data: Dynamic Panel Model for the Cigar DataMultivariate Modeling: Long-Term Temperature TrendsBivariate Model: Sales of Mink and Muskrat FursFactor Model: Now-Casting the US EconomyLongitudinal Data: Lung Function Analysis
Bivariate Basic Structural Model Panel Data: Random-Effects and Autoregressive ModelsBackcasting, Forecasting, and InterpolationLongitudinal Data: Smoothing of Repeated MeasuresA User-Defined Trend ModelModel with Multiple ARIMA ComponentsDynamic Factor ModelingDiagnostic Plots and Structural Break AnalysisLongitudinal Data: Variable Bandwidth SmoothingA Transfer Function Model for the Gas Furnace DataPanel Data: Dynamic Panel Model for the Cigar DataMultivariate Modeling: Long-Term Temperature TrendsBivariate Model: Sales of Mink and Muskrat FursFactor Model: Now-Casting the US EconomyLongitudinal Data: Lung Function Analysis - References
The SSM procedure complements several SAS/ETS procedures and the MIXED procedure in SAS/STAT software (see Chapter 65: The MIXED Procedure in SAS/STAT 13.2 User's Guide). The statistical models underlying all these procedures can be formulated as state space models; however, in many cases this formulation effort can be considerable. Generally speaking, when a problem can be formulated and satisfactorily solved either by using the SSM procedure or by using one of these other procedures, the other procedures are likely to be more efficient. However, in many instances, the SSM procedure can solve more general problems or offer more detailed analysis, or both. Throughout this discussion, it is assumed that the problem being solved can be modeled as a linear statistical model with Gaussian response variables. In particular, situations that require models such as autoregressive conditional heteroscedasticity (ARCH) models, and models with categorical response variables are not considered. The following list provides a more specific comparison of the SSM procedure with different procedures:
-
All the SAS/ETS time series analysis procedures (the ARIMA, ESM, UCM, VARMAX, STATESPACE, and PANEL procedures) require time series data and are not applicable to the longitudinal data.
-
For univariate time series analysis, the modeling facilities provided by the ARIMA, ESM, and UCM procedures are adequate in most cases. The SSM procedure can handle cases that do not fit neatly into one of these categories.
-
For multivariate time series data analysis, you can use the VARMAX procedure for vector ARIMA modeling and the STATESPACE procedure for state space modeling. The capabilities of the SSM procedure are complementary to these procedures. In particular, the predefined multivariate structural models available in the SSM procedure cannot be specified by either of these procedures. In addition, you can formulate a much wider range of multivariate models—for example, models for series with different frequencies, by using the SSM procedure.
-
When the
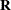 side effects are not too complicated (for example, if
side effects are not too complicated (for example, if 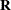 is diagonal), the model considered by the MIXED procedure is a special case of the model considered by the SSM procedure.
In the case of diagonal
is diagonal), the model considered by the MIXED procedure is a special case of the model considered by the SSM procedure.
In the case of diagonal 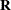 , it is easy to see that the state vector
, it is easy to see that the state vector 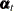 is equal to
is equal to 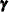 , the MIXED random-effects vector, for all
, the MIXED random-effects vector, for all 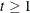 (that is,
(that is, 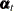 is time invariant). Therefore, the random-effects MIXED model is obtained by setting
is time invariant). Therefore, the random-effects MIXED model is obtained by setting 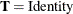 ,
, 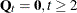 ,
, 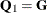 (the MIXED
(the MIXED 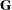 matrix), and
matrix), and 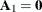 .
.
-
For the analysis of cross-sectional data, you can use the PANEL procedure. In this case, the SSM procedure capabilities are complementary. PROC SSM can provide alternate models, REML estimates, richer missing value support, and the estimates of the unobserved components (see the section Getting Started: SSM Procedure and the examples Example 27.2 and Example 27.11 for more information). In some situations the cross-sectional studies contain many panels but very few distinct time points. The PANEL procedure based analysis is better suited in such settings. In order for the analysis based on PROC SSM to be valid, the cross-sectional study must contain an adequate number of distinct time points.