The SSM Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 State Space Model and NotationTypes of Sequence DataOverview of Model Specification SyntaxFiltering, Smoothing, Likelihood, and Structural Break DetectionEstimation of User-Specified Linear Combination of State ElementsContrasting PROC SSM with Other SAS Procedures Predefined Trend ModelsPredefined Structural ModelsCovariance ParameterizationMissing ValuesComputational IssuesDisplayed OutputODS Table NamesODS Graph NamesOUT= Data Set
State Space Model and NotationTypes of Sequence DataOverview of Model Specification SyntaxFiltering, Smoothing, Likelihood, and Structural Break DetectionEstimation of User-Specified Linear Combination of State ElementsContrasting PROC SSM with Other SAS Procedures Predefined Trend ModelsPredefined Structural ModelsCovariance ParameterizationMissing ValuesComputational IssuesDisplayed OutputODS Table NamesODS Graph NamesOUT= Data Set -
Examples
 Bivariate Basic Structural Model Panel Data: Random-Effects and Autoregressive ModelsBackcasting, Forecasting, and InterpolationLongitudinal Data: Smoothing of Repeated MeasuresA User-Defined Trend ModelModel with Multiple ARIMA ComponentsDynamic Factor ModelingDiagnostic Plots and Structural Break AnalysisLongitudinal Data: Variable Bandwidth SmoothingA Transfer Function Model for the Gas Furnace DataPanel Data: Dynamic Panel Model for the Cigar DataMultivariate Modeling: Long-Term Temperature TrendsBivariate Model: Sales of Mink and Muskrat FursFactor Model: Now-Casting the US EconomyLongitudinal Data: Lung Function Analysis
Bivariate Basic Structural Model Panel Data: Random-Effects and Autoregressive ModelsBackcasting, Forecasting, and InterpolationLongitudinal Data: Smoothing of Repeated MeasuresA User-Defined Trend ModelModel with Multiple ARIMA ComponentsDynamic Factor ModelingDiagnostic Plots and Structural Break AnalysisLongitudinal Data: Variable Bandwidth SmoothingA Transfer Function Model for the Gas Furnace DataPanel Data: Dynamic Panel Model for the Cigar DataMultivariate Modeling: Long-Term Temperature TrendsBivariate Model: Sales of Mink and Muskrat FursFactor Model: Now-Casting the US EconomyLongitudinal Data: Lung Function Analysis - References
The model defined by the state space model equations (see the section State Space Model and Notation) is very general. This generality is quite useful because it encompasses a wide variety of data generation processes. On
the other hand, it also makes it easy to specify overly complex and numerically unstable models. If a suitable model is not
already known and you are in the early phases of modeling, it is important to start with models that are relatively simple
and well-behaved from the numerical standpoint. From the numerical and statistical considerations, two aspects of model formulation
are particularly important: identifiability and numerical stability. A model is identifiable if the observed data has a distinct
probability distribution for each admissible parameter vector. Unless proper care is taken, it is easy to specify an unidentifiable
state space model. Similarly, predictions according to some types of state space models can display explosive growth or wild
oscillations. This behavior is primarily governed by the transition matrix ![]() (or
(or ![]() in the time-varying case). Unidentifiable models can run into difficulties during parameter estimation, and explosive growth
(and wild oscillation) causes numerical problems associated with finite-precision arithmetic. Unfortunately, no simple identifiability
check is available for a general state space model, and it is difficult to decide at the outset whether a specified model
might suffer from numerical instability. See Harvey (1989, chap. 4, sec. 4) for a discussion of identifiability issues, and see Harvey (1989, chap. 3, sec. 3) for a discussion of the stability properties of time-invariant state space models. The following guidelines
are likely to result in models that are identifiable and numerically stable:
in the time-varying case). Unidentifiable models can run into difficulties during parameter estimation, and explosive growth
(and wild oscillation) causes numerical problems associated with finite-precision arithmetic. Unfortunately, no simple identifiability
check is available for a general state space model, and it is difficult to decide at the outset whether a specified model
might suffer from numerical instability. See Harvey (1989, chap. 4, sec. 4) for a discussion of identifiability issues, and see Harvey (1989, chap. 3, sec. 3) for a discussion of the stability properties of time-invariant state space models. The following guidelines
are likely to result in models that are identifiable and numerically stable:
-
Build models by composing submodels that are known to be well-behaved. The predefined models provided by the SSM procedure are good submodel candidates (see the sections Predefined Trend Models and Predefined Structural Models).
-
Pay careful attention to the way the variety of system matrices are defined. The behavior of their elements, as functions of model parameters and other variables, must be well-understood. If these elements are defined by using DATA steps, you can validate their behavior by running these DATA steps outside of the SSM procedure. In particular, note the following:
-
The transition matrix
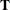 (or
(or 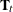 in the time-varying case) determines the explosiveness characteristics of the model; it must be well-behaved for all parameters.
in the time-varying case) determines the explosiveness characteristics of the model; it must be well-behaved for all parameters.
-
The disturbance covariances
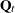 must be positive semidefinite for all parameters.
must be positive semidefinite for all parameters.
-
If the system matrices in the state equation, such as the transition matrix
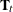 or the disturbance covariance
or the disturbance covariance 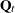 , are time-varying and the data contain replicate observations (observations with the same ID value), check that the elements
of these matrices do not vary during replicate observations. This follows from the fact that the underlying state does not
vary during replications (see the state equation in the section State Space Model and Notation and the section Types of Sequence Data).
, are time-varying and the data contain replicate observations (observations with the same ID value), check that the elements
of these matrices do not vary during replicate observations. This follows from the fact that the underlying state does not
vary during replications (see the state equation in the section State Space Model and Notation and the section Types of Sequence Data).
-